3.3 Trigonometric Substitution
Learning Objectives
- Solve integration problems involving the square root of a sum or difference of two squares.
In this section, we explore integrals containing expressions of the form ![]()
![]() and
and ![]() where the values of
where the values of ![]() are positive. We have already encountered and evaluated integrals containing some expressions of this type, but many still remain inaccessible. The technique of trigonometric substitution comes in very handy when evaluating these integrals. This technique uses substitution to rewrite these integrals as trigonometric integrals.
are positive. We have already encountered and evaluated integrals containing some expressions of this type, but many still remain inaccessible. The technique of trigonometric substitution comes in very handy when evaluating these integrals. This technique uses substitution to rewrite these integrals as trigonometric integrals.
Integrals Involving 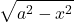
Before developing a general strategy for integrals containing ![]() consider the integral
consider the integral ![]() This integral cannot be evaluated using any of the techniques we have discussed so far. However, if we make the substitution
This integral cannot be evaluated using any of the techniques we have discussed so far. However, if we make the substitution ![]() where
where ![]() , we have
, we have ![]() After substituting into the integral, we get
After substituting into the integral, we get
![]()
After simplifying, we have
![]()
Because ![]() we obtain
we obtain
![]()
Since ![]() , we have that
, we have that ![]() and so
and so ![]() which implies
which implies
![]()
At this point, we can evaluate the integral using the techniques developed for integrating powers of products of trigonometric functions. Before completing this example, let’s take a look at the general theory behind this idea.
To evaluate integrals involving ![]() we make the substitution
we make the substitution ![]() and then
and then ![]() Let’s see why this actually makes sense. The domain of
Let’s see why this actually makes sense. The domain of ![]() is
is ![]() Thus,
Thus, ![]() Consequently,
Consequently, ![]() Since the range of
Since the range of ![]() over
over ![]() is
is ![]() there is a unique angle
there is a unique angle ![]() satisfying
satisfying ![]() so that
so that ![]() or equivalently, so that
or equivalently, so that ![]() If we substitute
If we substitute ![]() into
into ![]() we get
we get
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccc}\hfill \sqrt{{a}^{2}-{x}^{2}}&\ds =\sqrt{{a}^{2}-{\left(a\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \right)}^{2}}\hfill &\ds &\ds &\ds \text{Let}\phantom{\rule{0.2em}{0ex}}(x)=a\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.2em}{0ex}}\text{where}\phantom{\rule{0.2em}{0ex}}-\frac{\pi }{2}\le \theta \le \frac{\pi }{2}.\phantom{\rule{0.2em}{0ex}}\text{Simplify.}\hfill \\[5mm]\ds &\ds =\sqrt{{a}^{2}-{a}^{2}{\text{sin}}^{2}(\theta) }\hfill &\ds &\ds &\ds \text{Factor out}\phantom{\rule{0.2em}{0ex}}{a}^{2}.\hfill \\[5mm]\ds &\ds =\sqrt{{a}^{2}\left(1-{\text{sin}}^{2}(\theta) \right)}\hfill &\ds &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}1-{\text{sin}}^{2}(x)={\text{cos}}^{2}(x).\hfill \\[5mm]\ds &\ds =\sqrt{{a}^{2}{\text{cos}}^{2}(\theta) }\hfill &\ds &\ds &\ds \text{Take the square root.}\hfill \\[5mm]\ds &\ds =|a\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) |\hfill &\ds &\ds &\ds \\[5mm]\ds &\ds =a\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) .\hfill &\ds &\ds &\ds \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-923bd6b0ce9a97bad04ccf4ffd9b415f_l3.png)
Since ![]() on
on ![]() and
and ![]()
![]() From this discussion, we can see that by making the substitution
From this discussion, we can see that by making the substitution ![]() we are able to convert an integral involving a radical into an integral involving trigonometric functions. After we evaluate the integral, we can convert the solution back to an expression involving
we are able to convert an integral involving a radical into an integral involving trigonometric functions. After we evaluate the integral, we can convert the solution back to an expression involving ![]() To see how to do this, let’s begin by assuming that
To see how to do this, let’s begin by assuming that ![]() In this case,
In this case, ![]() Since
Since ![]() we can draw the reference triangle to assist in expressing the values of
we can draw the reference triangle to assist in expressing the values of ![]()
![]() and the remaining trigonometric functions in terms of
and the remaining trigonometric functions in terms of ![]() It can be shown that this triangle actually produces the correct values of the trigonometric functions evaluated at
It can be shown that this triangle actually produces the correct values of the trigonometric functions evaluated at ![]() for all
for all ![]() satisfying
satisfying ![]() It is useful to observe that the expression
It is useful to observe that the expression ![]() actually appears as the length of one side of the triangle. Last, should
actually appears as the length of one side of the triangle. Last, should ![]() appear by itself, we use
appear by itself, we use ![]()
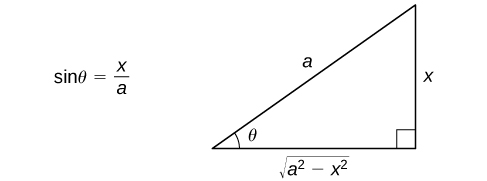
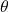 in terms of
in terms of 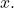
The essential part of this discussion is summarized in the following problem-solving strategy.
Problem-Solving Strategy: Integrating Expressions Involving 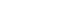
- It is a good idea to make sure the integral cannot be evaluated easily in another way. For example, although this method can be applied to integrals of the form
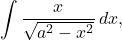 and
and 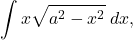 they can each be integrated directly by a simple substitution.
they can each be integrated directly by a simple substitution. - Make the substitution
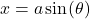 and
and 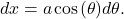
Note: This substitution yields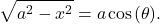
- Simplify the expression.
- Evaluate the integral using techniques from the section on trigonometric integrals.
- Use the reference triangle from Figure 1 to rewrite the result in terms of
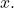 You may also need to use some trigonometric identities and the relationship
You may also need to use some trigonometric identities and the relationship 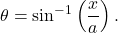
The following example demonstrates the application of this problem-solving strategy.
Integrating an Expression Involving 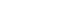
Evaluate ![]()
Solution
Begin by making the substitutions ![]() and
and ![]() Since
Since ![]() we can construct the reference triangle shown in the following figure.
we can construct the reference triangle shown in the following figure.
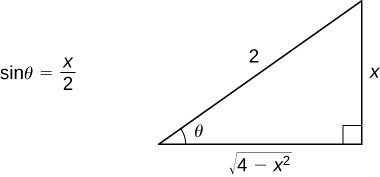
Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccc}\hfill \ds{\int }^{\text{}}\sqrt{4-{x}^{2}}\phantom{\rule{0.1em}{0ex}}\,dx &\ds ={\int }^{\text{}}\sqrt{4-{\left(2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \right)}^{2}}\,2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta \hfill &\ds &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}x=2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}\,dx =2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta .\hfill \\[5mm]\ds &\ds ={\int }^{\text{}}\sqrt{4\left(1-{\text{sin}}^{2}(\theta) \right)}\,2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta \hfill &\ds &\ds &\ds \text{Simplify.}\hfill \\[5mm]\ds &\ds ={\int }^{\text{}}\sqrt{4\phantom{\rule{0.1em}{0ex}}{\text{cos}}^{2}(\theta) }2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta \hfill &\ds &\ds &\ds \text{Use the identity}\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{2}(\theta) =1-{\text{sin}}^{2}(\theta) .\hfill \\[5mm]\ds &\ds ={\int }^{\text{}}2|\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) |2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta \hfill &\ds &\ds &\ds \text{Take the square root.}\hfill \\[5mm]\ds &\ds ={\int }^{\text{}}4\phantom{\rule{0.1em}{0ex}}{\text{cos}}^{2}(\theta) d\theta \hfill &\ds &\ds &\ds \begin{array}{l}\text{Simplify. Since}\phantom{\rule{0.2em}{0ex}}-\frac{\pi }{2}\le \theta \le \frac{\pi }{2},\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) \ge 0\phantom{\rule{0.2em}{0ex}}\text{and}\hfill \\[5mm]\ds |\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) |=\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) .\hfill \end{array}\hfill \\[5mm]\ds &\ds ={\int }^{\text{}}4\left(\frac{1}{2}+\frac{1}{2}\text{cos}\left(2\theta \right)\right)d\theta \hfill &\ds &\ds &\ds \begin{array}{l}\text{Use the strategy for integrating an even power}\hfill \\[5mm]\ds \text{of}\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) .\hfill \end{array}\hfill \\[5mm]\ds &\ds =2\theta +\text{sin}\left(2\theta \right)+C\hfill &\ds &\ds &\ds \text{Evaluate the integral.}\hfill \\[5mm]\ds &\ds =2\theta +\left(2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) \right)+C\hfill &\ds &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}\text{sin}\left(2\theta \right)=2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) .\hfill \\[5mm]\ds &\ds =2{\text{sin}}^{-1}\left(\frac{x}{2}\right)+2\cdot \frac{x}{2}\cdot \frac{\sqrt{4-{x}^{2}}}{2}+C\hfill &\ds &\ds &\ds \begin{array}{l}\text{Substitute}\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{-1}\left(\frac{x}{2}\right)=\theta \phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) =\frac{x}{2}.\phantom{\rule{0.2em}{0ex}}\text{Use}\hfill \\[5mm]\ds \text{the reference triangle to see that}\hfill \\[5mm]\ds \text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) =\frac{\sqrt{4-{x}^{2}}}{2}\phantom{\rule{0.2em}{0ex}}\text{and make this substitution.}\hfill \end{array}\hfill \\[5mm]\ds &\ds =2{\text{sin}}^{-1}\left(\frac{x}{2}\right)+\frac{x\sqrt{4-{x}^{2}}}{2}+C.\hfill &\ds &\ds &\ds \text{Simplify.}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-a843a824a471a39431ceba412ae71f53_l3.png)
Integrating an Expression Involving 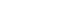
Evaluate ![]()
Solution
First make the substitutions ![]() and
and ![]() Since
Since ![]() we can construct the reference triangle shown in Figure 3 below.
we can construct the reference triangle shown in Figure 3 below.

Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccc}\hfill \ds\int \frac{\sqrt{4-{x}^{2}}}{x}\,dx &\ds =\int \frac{\sqrt{4-{\left(2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \right)}^{2}}}{2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) }2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta \hfill &\ds &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}x=2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}dx=2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta .\hfill \\[5mm]\ds &\ds =\int \frac{2\phantom{\rule{0.1em}{0ex}}{\text{cos}}^{2}(\theta) }{\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) }d\theta \hfill &\ds &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}} 1-{\text{sin}}^{2}(\theta)={\text{cos}}^{2}(\theta) \phantom{\rule{0.2em}{0ex}}\text{and simplify.}\hfill \\[5mm]\ds &\ds =\int \frac{2\left(1-{\text{sin}}^{2}(\theta) \right)}{\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) }d\theta \hfill &\ds &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{2}(\theta) =1-{\text{sin}}^{2}(\theta) .\hfill \\[5mm]\ds &\ds ={\int }^{\text{}}\left(2\phantom{\rule{0.1em}{0ex}}\text{csc}\phantom{\rule{0.1em}{0ex}}(\theta) -2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \right)d\theta \hfill &\ds &\ds &\ds \begin{array}{c}\text{Separate the numerator, simplify, and use}\hfill \\[5mm]\ds \text{csc}\phantom{\rule{0.1em}{0ex}}(\theta) =\frac{1}{\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) }.\hfill \end{array}\hfill \\[5mm]\ds &\ds =2\phantom{\rule{0.1em}{0ex}}\text{ln}|\text{csc}\phantom{\rule{0.1em}{0ex}}(\theta) -\text{cot}\phantom{\rule{0.1em}{0ex}}(\theta) |+2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) +C\hfill &\ds &\ds &\ds \text{Evaluate the integral.}\hfill \\[5mm]\ds &\ds =2\phantom{\rule{0.1em}{0ex}}\text{ln}\left|\frac{2}{x}-\frac{\sqrt{4-{x}^{2}}}{x}\right|+\sqrt{4-{x}^{2}}+C.\hfill &\ds &\ds &\ds \begin{array}{c}\text{Use the reference triangle to rewrite the}\hfill \\[5mm]\ds \text{expression in terms of}\phantom{\rule{0.2em}{0ex}}x\phantom{\rule{0.2em}{0ex}}\text{and simplify.}\hfill \end{array}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-a55bf345ac935361644cd5fcacc8fded_l3.png)
In the next example, we see that we sometimes have a choice of methods.
Integrating an Expression Involving 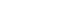 Two Ways
Two Ways
Evaluate ![]() two ways: first by using the substitution
two ways: first by using the substitution ![]() and then by using a trigonometric substitution.
and then by using a trigonometric substitution.
Solution
Method 1
Let ![]() and hence
and hence ![]() Thus,
Thus, ![]() In this case, the integral becomes
In this case, the integral becomes
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccc}\hfill {\int }^{\text{}}{x}^{3}\sqrt{1-{x}^{2}}\phantom{\rule{0.1em}{0ex}}\,dx &\ds =-\frac{1}{2}{\int }^{\text{}}{x}^{2}\sqrt{1-{x}^{2}}\left(-2x\phantom{\rule{0.1em}{0ex}}\,dx \right)\hfill &\ds &\ds &\ds \text{Make the substitution.}\hfill \\[5mm]\ds &\ds =-\frac{1}{2}{\int }^{\text{}}\left(1-u\right)\sqrt{u}\phantom{\rule{0.1em}{0ex}}du\hfill &\ds &\ds &\ds \text{Expand the expression.}\hfill \\[5mm]\ds &\ds =-\frac{1}{2}\int \left({u}^{1\text{/}2}-{u}^{3\text{/}2}\right)du\hfill &\ds &\ds &\ds \text{Evaluate the integral.}\hfill \\[5mm]\ds &\ds =-\frac{1}{2}\left(\frac{2}{3}{u}^{3\text{/}2}-\frac{2}{5}{u}^{5\text{/}2}\right)+C\hfill &\ds &\ds &\ds \text{Rewrite in terms of}\phantom{\rule{0.2em}{0ex}}(x).\hfill \\[5mm]\ds &\ds =-\frac{1}{3}{\left(1-{x}^{2}\right)}^{3\text{/}2}+\frac{1}{5}{\left(1-{x}^{2}\right)}^{5\text{/}2}+C.\hfill &\ds &\ds &\ds \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-5992bead8ee7182c1a04eac0e5e942cf_l3.png)
Method 2
Let ![]() In this case,
In this case, ![]() Using this substitution, we have
Using this substitution, we have
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccc}\hfill {\int }^{\text{}}{x}^{3}\sqrt{1-{x}^{2}}\phantom{\rule{0.1em}{0ex}}\,dx &\ds ={\int }^{\text{}}{\text{sin}}^{3}(\theta) \phantom{\rule{0.1em}{0ex}}{\text{cos}}^{2}(\theta) d\theta \hfill &\ds &\ds &\ds \hfill\\[5mm]\ds &\ds ={\int }^{\text{}}\left(1-{\text{cos}}^{2}(\theta) \right){\text{cos}}^{2}(\theta) \phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta \hfill &\ds &\ds &\ds \text{Let}\phantom{\rule{0.2em}{0ex}}u=\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) .\phantom{\rule{0.2em}{0ex}}\text{Thus,}\phantom{\rule{0.2em}{0ex}}du= - \text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta.\hfill \\[5mm]\ds &\ds ={\int }^{\text{}}\left({u}^{4}-{u}^{2}\right)du\hfill &\ds &\ds &\ds \\[5mm]\ds &\ds =\frac{1}{5}{u}^{5}-\frac{1}{3}{u}^{3}+C\hfill &\ds &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}u=\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta).\hfill \\[5mm]\ds &\ds =\frac{1}{5}{\text{cos}}^{5}(\theta) -\frac{1}{3}{\text{cos}}^{3}(\theta) +C\hfill &\ds &\ds &\ds \begin{array}{c}\text{Use a reference triangle to see that}\hfill \\[5mm]\ds \text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) =\sqrt{1-{x}^{2}}.\hfill \end{array}\hfill \\[5mm]\ds &\ds =\frac{1}{5}{\left(1-{x}^{2}\right)}^{5\text{/}2}-\frac{1}{3}{\left(1-{x}^{2}\right)}^{3\text{/}2}+C.\hfill &\ds &\ds &\ds \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-b8de981a42dd24448f12b0b32eb0b48c_l3.png)
Rewrite the integral ![]() using the appropriate trigonometric substitution (do not evaluate the integral).
using the appropriate trigonometric substitution (do not evaluate the integral).
Answer
![]()
Hint
Substitute ![]() and
and ![]()
Integrating Expressions Involving 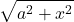
For integrals containing ![]() let’s first consider the domain of this expression. Since
let’s first consider the domain of this expression. Since ![]() is defined for all real values of
is defined for all real values of ![]() we restrict our choice to those trigonometric functions that have a range of all real numbers. Thus, our choice is restricted to selecting either
we restrict our choice to those trigonometric functions that have a range of all real numbers. Thus, our choice is restricted to selecting either ![]() or
or ![]() Either of these substitutions would actually work, but the standard substitution is
Either of these substitutions would actually work, but the standard substitution is ![]() or, equivalently,
or, equivalently, ![]() With this substitution, we make the assumption that
With this substitution, we make the assumption that ![]() so that we also have
so that we also have ![]() The procedure for using this substitution is outlined in the following problem-solving strategy.
The procedure for using this substitution is outlined in the following problem-solving strategy.
Problem-Solving Strategy: Integrating Expressions Involving 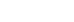
- Check to see whether the integral can be evaluated easily by using another method. In some cases, it is more convenient to use an alternative method.
- Substitute
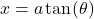 and
and 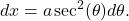 This substitution yields
This substitution yields
![Rendered by QuickLaTeX.com \ds \begin{array}{ll}\ds\sqrt{{a}^{2}+{x}^{2}}&=\sqrt{{a}^{2}+{\left(a\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) \right)}^{2}}=\sqrt{{a}^{2}\left(1+{\text{tan}}^{2}(\theta) \right)}=\sqrt{{a}^{2}{\text{sec}}^{2}(\theta) }\hfill \\[1mm]&=|a\phantom{\rule{0.1em}{0ex}}\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) |=a\phantom{\rule{0.1em}{0ex}}\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) .\hfill\end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-c3e504a19f554d50e5f2e6db18125499_l3.png)
(Since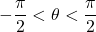 and
and 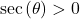 over this interval,
over this interval, 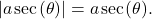 )
) - Simplify the expression.
- Evaluate the integral using techniques from the section on trigonometric integrals.
- Use the reference triangle from to rewrite the result in terms of
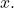 You may also need to use some trigonometric identities and the relationship
You may also need to use some trigonometric identities and the relationship 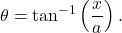
(Note: The reference triangle is based on the assumption that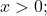 however, the trigonometric ratios produced from the reference triangle are the same as the ratios for which
however, the trigonometric ratios produced from the reference triangle are the same as the ratios for which 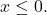
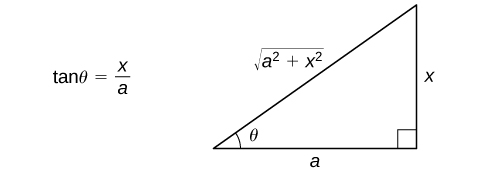
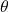 in terms of
in terms of 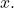
Integrating an Expression Involving 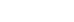
Evaluate ![]() and check the solution by differentiating.
and check the solution by differentiating.
Solution
Begin with the substitution ![]() and
and ![]() Since
Since ![]() draw the reference triangle in the following figure.
draw the reference triangle in the following figure.
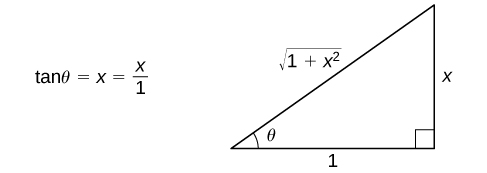
Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccc}\ds\hfill \int \frac{\,dx }{\sqrt{1+{x}^{2}}}&\ds =\int \frac{{\text{sec}}^{2}(\theta) }{\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) }d\theta \hfill &\ds &\ds &\ds \begin{array}{c}\text{Substitute}\phantom{\rule{0.2em}{0ex}}x=\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}\,dx ={\text{sec}}^{2}(\theta) d\theta .\phantom{\rule{0.2em}{0ex}}\text{This}\hfill \\[5mm]\ds \text{substitution makes}\phantom{\rule{0.2em}{0ex}}\sqrt{1+{x}^{2}}=\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) .\phantom{\rule{0.2em}{0ex}}\text{Simplify.}\hfill \end{array}\hfill \\[5mm]\ds &\ds ={\int }^{\text{}}\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta \hfill &\ds &\ds &\ds \text{Evaluate the integral.}\hfill \\[5mm]\ds &\ds =\text{ln}|\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) +\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) |+C\hfill &\ds &\ds &\ds \begin{array}{c}\text{Use the reference triangle to express the result}\hfill \\[5mm]\ds \text{in terms of}\phantom{\rule{0.2em}{0ex}}x.\hfill \end{array}\hfill \\[5mm]\ds &\ds =\text{ln}\left|\sqrt{1+{x}^{2}}+x\right|+C.\hfill &\ds &\ds &\ds \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-8b70fd61e7f4747984e1029012d563d2_l3.png)
To check the solution, differentiate:
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill \frac{d}{\,dx }\left(\text{ln}|\sqrt{1+{x}^{2}}+x|\right)&\ds =\frac{1}{\sqrt{1+{x}^{2}}+x}\cdot \left(\frac{x}{\sqrt{1+{x}^{2}}}+1\right)\hfill \\[5mm]\ds &\ds =\frac{1}{\sqrt{1+{x}^{2}}+x}\cdot \frac{x+\sqrt{1+{x}^{2}}}{\sqrt{1+{x}^{2}}}\hfill \\[5mm]\ds &\ds =\frac{1}{\sqrt{1+{x}^{2}}}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-6ccb8914ea2110c24b607280f8654659_l3.png)
Since ![]() for all values of
for all values of ![]() we could rewrite
we could rewrite ![]() if desired.
if desired.
Evaluating 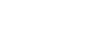 Using a Different Substitution
Using a Different Substitution
Use the substitution ![]() to evaluate
to evaluate ![]()
Solution
Because ![]() has a range of all real numbers, and
has a range of all real numbers, and ![]() we may also use the substitution
we may also use the substitution ![]() to evaluate this integral. In this case,
to evaluate this integral. In this case, ![]() Consequently,
Consequently,
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccc}\hfill \ds\int \frac{\,dx }{\sqrt{1+{x}^{2}}}&\ds =\int \frac{\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) }{\sqrt{1+{\text{sinh}}^{2}(\theta) }}d\theta \hfill &\ds &\ds &\ds \begin{array}{c}\text{Substitute}\phantom{\rule{0.2em}{0ex}}x=\text{sinh}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}\,dx =\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta .\hfill \\[5mm]\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}1+{\text{sinh}}^{2}(\theta) ={\text{cosh}}^{2}(\theta) .\hfill \end{array}\hfill \\[5mm]\ds &\ds =\int \frac{\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) }{\sqrt{{\text{cosh}}^{2}(\theta) }}d\theta \hfill &\ds &\ds &\ds \sqrt{{\text{cosh}}^{2}(\theta) }=|\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) |\hfill \\[5mm]\ds &\ds =\int \frac{\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) }{|\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) |}d\theta \hfill &\ds &\ds &\ds |\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) |=\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.2em}{0ex}}\text{since}\phantom{\rule{0.2em}{0ex}}\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) \symbol{"3E}0\phantom{\rule{0.2em}{0ex}}\text{for all}\phantom{\rule{0.2em}{0ex}}(\theta) .\hfill \\[5mm]\ds &\ds =\int \frac{\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) }{\text{cosh}\phantom{\rule{0.1em}{0ex}}(\theta) }d\theta \hfill &\ds &\ds &\ds \text{Simplify.}\hfill \\[5mm]\ds &\ds ={\int }^{\text{}}1d\theta \hfill &\ds &\ds &\ds \text{Evaluate the integral.}\hfill \\[5mm]\ds &\ds =\theta +C\hfill &\ds &\ds &\ds \text{Since}\phantom{\rule{0.2em}{0ex}}x=\text{sinh}\phantom{\rule{0.1em}{0ex}}(\theta) ,\phantom{\rule{0.2em}{0ex}}\text{we know}\phantom{\rule{0.2em}{0ex}}(\theta) ={\text{sinh}}^{-1}(x).\hfill \\[5mm]\ds &\ds ={\text{sinh}}^{-1}(x)+C.\hfill &\ds &\ds &\ds \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-a3ee0841e4e2ea83292b3dd3eb8f22ec_l3.png)
Analysis
This answer looks quite different from the answer obtained using the substitution ![]() To see that the solutions are the same, set
To see that the solutions are the same, set ![]() Then
Then ![]() that is,
that is,
![]()
After multiplying both sides by ![]() and rewriting, this equation becomes:
and rewriting, this equation becomes:
![]()
Use the quadratic equation formula to solve for ![]()
![]()
Simplifying, we have:
![]()
Since ![]() it must be the case that
it must be the case that ![]() Therefore,
Therefore,
![]()
At last, we obtain
![]()
After we make the final observation that, since ![]()
![]()
we see that the two different methods produced the same solutions.
Finding an Arc Length
Find the length of the curve ![]() over the interval
over the interval ![]()
Solution
Because ![]() the arc length is given by
the arc length is given by
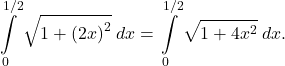
To evaluate this integral, use the substitution ![]() and
and ![]() We also need to change the limits of integration. If
We also need to change the limits of integration. If ![]() then
then ![]() and if
and if ![]() then
then ![]() Thus,
Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccc}\hfill \ds\int\limits_{0}^{1\text{/}2}\sqrt{1+4{x}^{2}}\phantom{\rule{0.1em}{0ex}}\,dx &\ds =\int\limits_{0}^{\pi \text{/}4}\sqrt{1+{\text{tan}}^{2}(\theta) }\,\frac{1}{2}{\text{sec}}^{2}(\theta) d\theta \hfill &\ds &\ds &\ds \begin{array}{c}\text{After substitution,}\hfill \\[5mm]\ds \sqrt{1+4{x}^{2}}=\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) .\phantom{\rule{0.2em}{0ex}}\text{Substitute}\hfill \\[5mm]\ds 1+{\text{tan}}^{2}(\theta) ={\text{sec}}^{2}(\theta) \phantom{\rule{0.2em}{0ex}}\text{and simplify.}\hfill \end{array}\hfill \\[5mm]\ds &\ds =\frac{1}{2}\int\limits_{0}^{\pi \text{/}4}{\text{sec}}^{3}(\theta) d\theta \hfill &\ds &\ds &\ds \begin{array}{c}\text{We derived this integral in the}\hfill \\[5mm]\ds \text{previous section.}\hfill \end{array}\hfill \\[5mm]\ds &\ds =\frac{1}{2}\left(\frac{1}{2}\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) +\frac12\text{ln}|\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) +\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) |\right)\Big|_0^{\pi\text{/}4}\hfill &\ds &\ds &\ds \text{Evaluate and simplify.}\hfill \\[5mm]\ds &\ds =\frac{1}{4}\left(\sqrt{2}+\text{ln}\left(\sqrt{2}+1\right)\right).\hfill &\ds &\ds &\ds \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-8fd4036bfdbfbc9bb6d180d996a98864_l3.png)
Rewrite ![]() by using a substitution involving
by using a substitution involving ![]()
Answer
![]()
Hint
Use ![]() and
and ![]()
Integrating Expressions Involving 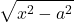
The domain of the expression ![]() is
is ![]() Thus, either
Thus, either ![]() or
or ![]() Hence,
Hence, ![]() or
or ![]() Since these intervals correspond to the range of
Since these intervals correspond to the range of ![]() on the set
on the set ![]() it makes sense to use the substitution
it makes sense to use the substitution ![]() or, equivalently,
or, equivalently, ![]() where
where ![]() or
or ![]() The corresponding substitution for
The corresponding substitution for ![]() is
is ![]() The procedure for using this substitution is outlined in the following problem-solving strategy.
The procedure for using this substitution is outlined in the following problem-solving strategy.
Problem-Solving Strategy: Integrals Involving 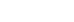
- Check to see whether the integral cannot be evaluated using another method. If so, we may wish to consider applying an alternative technique.
- Substitute
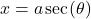 and
and 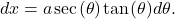 This substitution yields
This substitution yields
![Rendered by QuickLaTeX.com \begin{array}{ll}\ds \sqrt{{x}^{2}-{a}^{2}}&=\sqrt{{\left(a\phantom{\rule{0.1em}{0ex}}\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) \right)}^{2}-{a}^{2}}=\sqrt{{a}^{2}\left({\text{sec}}^{2}(\theta) -1\right)}=\sqrt{{a}^{2}{\text{tan}}^{2}(\theta) }\\[1mm]&=a\phantom{\rule{0.1em}{0ex}}|\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) |.\end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-c110ccfc640daaca4bffd72c000a1066_l3.png)
For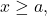 we have
we have 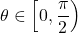 , which implies that
, which implies that 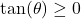 , and so
, and so 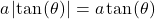 while for
while for 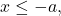
![Rendered by QuickLaTeX.com \ds\theta\in\left(\frac{\pi}2,\pi\right]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-2194c22fc9f37dccb93ccc7c555cd3f5_l3.png) , implying that
, implying that 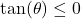 , and hence
, and hence 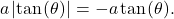
- Simplify the expression.
- Evaluate the integral using techniques from the section on trigonometric integrals.
- Use the reference triangles to rewrite the result in terms of
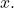 You may also need to use some trigonometric identities and the relationship
You may also need to use some trigonometric identities and the relationship 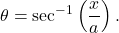
(Note: We need both reference triangles, since the values of some of the trigonometric ratios are different depending on whether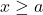 or
or 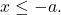 )
)
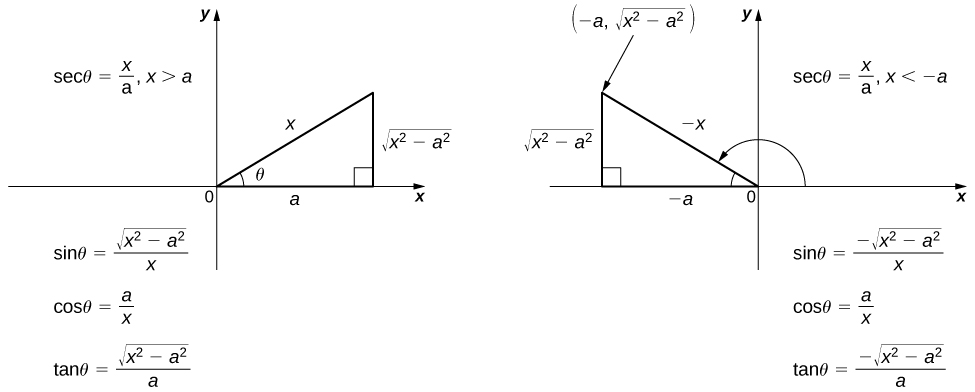
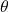 in terms of
in terms of 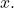
Finding the Area of a Region
Find the area of the region between the graph of ![]() and the x-axis over the interval
and the x-axis over the interval ![]()
Solution
First, sketch a rough graph of the region described in the problem, as shown in the following figure.
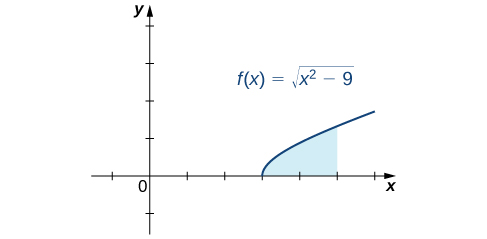
We can see that the area is 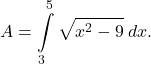 To evaluate this definite integral, substitute
To evaluate this definite integral, substitute ![]() and
and ![]() We must also change the limits of integration. If
We must also change the limits of integration. If ![]() then
then ![]() and hence
and hence ![]() If
If ![]() then
then ![]() After making these substitutions and simplifying, we have
After making these substitutions and simplifying, we have
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccc}\hfill \text{Area}&\ds =\int\limits_{3}^{5}\sqrt{{x}^{2}-9}\phantom{\rule{0.1em}{0ex}}\,dx \hfill &\ds &\ds &\ds \\[5mm]\ds &\ds =\int\limits_{0}^{{\text{sec}}^{-1}\left(5\text{/}3\right)}9\phantom{\rule{0.1em}{0ex}}{\text{tan}}^{2}(\theta) \phantom{\rule{0.1em}{0ex}}\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta \hfill &\ds &\ds &\ds \phantom{\rule{0.2em}{0ex}}{\text{tan}}^{2}(\theta) =1-{\text{sec}}^{2}(\theta) .\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{{\text{sec}}^{-1}\left(5\text{/}3\right)}9\left({\text{sec}}^{2}(\theta) -1\right)\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) d\theta \hfill &\ds &\ds &\ds \text{Expand.}\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{{\text{sec}}^{-1}\left(5\text{/}3\right)}9\left({\text{sec}}^{3}(\theta) -\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) \right)d\theta \hfill &\ds &\ds &\ds \text{Evaluate the integral.}\hfill \\[5mm]\ds &\ds =\left(\frac{9}{2}\text{ln}|\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) +\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) |+\frac{9}{2}\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) \right)-9\phantom{\rule{0.1em}{0ex}}\text{ln}|\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) +\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) |\Big|_0^{\sec^{-1}(5\text{/}3)}\hfill &\ds &\ds &\ds \text{Simplify.}\hfill \\[5mm]\ds &\ds =\frac{9}{2}\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) \phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) -\frac{9}{2}\text{ln}|\text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) +\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) |\Big|_0^{\sec^{-1}(5\text{/}3)}\hfill &\ds &\ds &\ds \begin{array}{l}\text{Evaluate. Use that}\\[5mm]\phantom{\rule{0.2em}{0ex}}\text{sec}\left({\text{sec}}^{-1}\left(\frac{5}{3}\right)\right)=\frac{5}{3}\hfill \\[5mm]\ds \text{and}\phantom{\rule{0.2em}{0ex}}\text{tan}\left({\text{sec}}^{-1}\left(\frac{5}{3}\right)\right)=\frac{4}{3}.\hfill \end{array}\hfill \\[5mm]\ds &\ds =\frac{9}{2}\cdot \frac{5}{3}\cdot \frac{4}{3}-\frac{9}{2}\text{ln}\left|\frac{5}{3}+\frac{4}{3}\right|-\left(\frac{9}{2}\cdot 1\cdot 0-\frac{9}{2}\text{ln}|1+0|\right)\hfill &\ds &\ds &\ds \\[5mm]\ds &\ds =10-\frac{9}{2}\text{ln}\phantom{\rule{0.1em}{0ex}}3.\hfill &\ds &\ds &\ds \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-0279acab2c3ad4d479075a40197e0476_l3.png)
Evaluate ![]() Assume that
Assume that ![]()
Answer
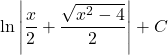
Hint
Substitute ![]() and
and ![]()
Key Concepts
- For integrals involving
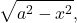 use the substitution
use the substitution 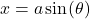 and
and 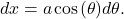
- For integrals involving
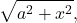 use the substitution
use the substitution 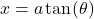 and
and 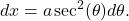
- For integrals involving
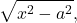 substitute
substitute 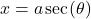 and
and 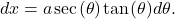
Exercises
Simplify the following expressions by writing each one using a single trigonometric function.
1. ![]()
Answer
![]()
2. ![]()
3. ![]()
Answer
![]()
4. ![]()
Use the technique of completing the square to express each quadratic polynomial in the form ![]() .
.
5. ![]()
Answer
![]()
6. ![]()
7. ![]()
Answer
![]()
Evaluate the following integrals using the method of trigonometric substitution.
8. ![]()
9. ![]() (
(![]() )
)
Answer
![]()
10. 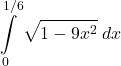
11. ![]()
Answer
![]()
12. 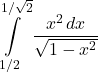
13. ![]()
Answer
![]()
14. ![]()
15. 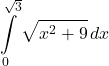
Answer
![]()
(Hint: ![]() .)
.)
16. 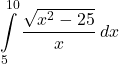
17. ![]()
Answer
![]()
18. ![]()
(Hint: factor a power of ![]() out of the root.)
out of the root.)
19. 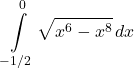
(Hint: when factoring a power of ![]() out of the root, be careful with the signs.)
out of the root, be careful with the signs.)
Answer
![]()
20. 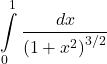
21. ![]()
Answer
![]()
22. ![]()
23. ![]()
Answer
![]()
24. ![]()
25. ![]()
Answer
![]()
26. ![]()
27. 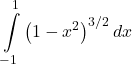
Answer
![]()
In the following exercises, use the substitutions ![]() or
or ![]() Express the final answers in terms of the variable x.
Express the final answers in terms of the variable x.
28. ![]()
29. ![]()
Answer
![]()
30. ![]()
31. ![]()
Answer
![]()
32. ![]()
33. ![]()
Answer
![]()
Combine the technique of completing the square with a trignometric substitution to evaluate the following integrals.
34. ![]()
35. ![]()
Answer
![]()
36. ![]()
37. ![]()
Answer
![]()
38. ![]()
39. Evaluate the integral 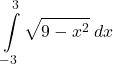 using geometry.
using geometry.
Answer
![]() area of a semicircle with radius 3
area of a semicircle with radius 3
40. Find the area enclosed by the ellipse ![]()
41. Evaluate the integral ![]() using two different substitutions. First, let
using two different substitutions. First, let ![]() and evaluate using trigonometric substitution. Second, let
and evaluate using trigonometric substitution. Second, let ![]() and use trigonometric substitution. Are the answers the same?
and use trigonometric substitution. Are the answers the same?
Answer
![]() and
and ![]() ; these answers are the same since
; these answers are the same since ![]() and
and ![]() is a constant.
is a constant.
42. Evaluate the integral ![]() using the substitution
using the substitution ![]() Next, evaluate the same integral using the substitution
Next, evaluate the same integral using the substitution ![]() Show that the results are equivalent.
Show that the results are equivalent.
43. Evaluate the integral ![]() using the form
using the form ![]() Next, evaluate the same integral using
Next, evaluate the same integral using ![]() Are the results the same?
Are the results the same?
Answer
![]() is the result using either method.
is the result using either method.
44. State the method of integration you would use to evaluate the integral ![]() Why did you choose this method?
Why did you choose this method?
45. State the method of integration you would use to evaluate the integral ![]() Why did you choose this method?
Why did you choose this method?
Answer
Use trigonometric substitution ![]()
46. Find the area bounded by ![]()
47. During each cycle, the velocity v (in feet per second) of a robotic welding device is given by ![]() where t is time in seconds. Find the expression for the displacement s (in feet) as a function of t if
where t is time in seconds. Find the expression for the displacement s (in feet) as a function of t if ![]() when
when ![]()
Answer
![]()
48. An oil storage tank can be described as the volume generated by revolving the area bounded by ![]() about the x-axis. Find the volume of the tank (in cubic meters).
about the x-axis. Find the volume of the tank (in cubic meters).
49. The region bounded by the graph of ![]() and the x-axis between
and the x-axis between ![]() and
and ![]() is revolved about the x-axis. Find the volume of the solid that is generated.
is revolved about the x-axis. Find the volume of the solid that is generated.
Answer
![]()
50. Find the length of the arc of the curve ![]() over the interval
over the interval ![]()
51. Find the length of the curve ![]() between
between ![]() and
and ![]()
Answer
![]()
52. Find the area of the surface generated by revolving the curve ![]() from
from ![]() about the y-axis.
about the y-axis.
Glossary
- trigonometric substitution
- an integration technique that converts an algebraic integral containing expressions of the form
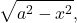
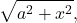 or
or 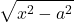 into a trigonometric integral
into a trigonometric integral

