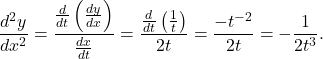7.2 Calculus of Parametric Curves
Learning Objectives
- Determine derivatives and equations of tangents for parametric curves.
- Find the area under a parametric curve.
- Determine the arc length of a parametric curve.
- Apply the formula for the surface area of the surface generated by revolving a parametric curve about the x-axis or the y-axis.
Now that we have introduced the concept of a parameterized curve, our next step is to learn how to work with this concept in the context of calculus. For example, if we know a parameterization of a given curve, is it possible to calculate the slope of a tangent line to the curve? How about the arc length of the curve? Or the area under the curve?
Another scenario: Suppose we would like to represent the location of a baseball after the ball leaves a pitcher’s hand. If the position of the baseball is represented by the plane curve ![]() then we should be able to use calculus to find the speed of the ball at any given time. Furthermore, we should be able to calculate just how far that ball has traveled as a function of time.
then we should be able to use calculus to find the speed of the ball at any given time. Furthermore, we should be able to calculate just how far that ball has traveled as a function of time.
Derivatives of Parametric Equations
We start by asking how to calculate the slope of a line tangent to a parametric curve at a point. Consider the plane curve defined by the parametric equations
![]()
The graph of this curve appears in Figure 1 below. It is a line segment starting at ![]() and ending at
and ending at ![]()
We can eliminate the parameter by first solving the equation ![]() for t:
for t:
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill x\left(t\right)&\ds =\hfill &\ds 2t+3\hfill \\[5mm]\ds \hfill x-3&\ds =\hfill &\ds 2t\hfill \\[5mm]\ds \hfill t&\ds =\hfill &\ds \frac{x-3}{2}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-1aad1e1df9b2c7c940cae20cde6f0a23_l3.png)
Substituting this into ![]() we obtain
we obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill y\left(t\right)&\ds =\hfill &\ds 3t-4\hfill \\[5mm]\ds \hfill y&\ds =\hfill &\ds 3\left(\frac{x-3}{2}\right)-4\hfill \\[5mm]\ds \hfill y&\ds =\hfill &\ds \frac{3x}{2}-\frac{9}{2}-4\hfill \\[5mm]\ds \hfill y&\ds =\hfill &\ds \frac{3x}{2}-\frac{17}{2}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-de751983656bdf9b5a8d11cd44682416_l3.png)
The slope of this line is given by ![]() Next we calculate
Next we calculate ![]() and
and ![]() This gives
This gives ![]() and
and ![]() Notice that
Notice that 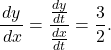 This is no coincidence, as outlined in the following theorem.
This is no coincidence, as outlined in the following theorem.
Derivative of Parametric Equations
Consider the plane curve defined by the parametric equations ![]() and
and ![]() Suppose that
Suppose that ![]() and
and ![]() exist, and assume that
exist, and assume that ![]() Then the derivative
Then the derivative ![]() is given by
is given by
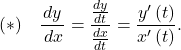
Proof
This theorem can be proven using the Chain Rule. In particular, assume that the parameter t can be eliminated, yielding a differentiable function ![]() Then
Then ![]() Differentiating both sides of this equation using the Chain Rule yields
Differentiating both sides of this equation using the Chain Rule yields
![]() so
so
![]()
But ![]() which proves the theorem. □
which proves the theorem. □
The formula (*) from the previous theorem can be used to calculate the first derivative for a curve defined parametrically at the given value ![]() of
of ![]() , and hence the slope of the tangent line to the curve at the point
, and hence the slope of the tangent line to the curve at the point ![]() corresponding to
corresponding to ![]() . For the purpose of sketching parametric curves, it is useful to determine, where the tangent to the curve is horizontal and where it is vertical. It has a direct analogy with considering the critical points on the graph of a curve with explicit equation
. For the purpose of sketching parametric curves, it is useful to determine, where the tangent to the curve is horizontal and where it is vertical. It has a direct analogy with considering the critical points on the graph of a curve with explicit equation ![]() , corresponding to the values
, corresponding to the values ![]() of
of ![]() , such that
, such that ![]() or
or ![]() is undefined. Based on (*), we see that the tangent to the parametric curve
is undefined. Based on (*), we see that the tangent to the parametric curve ![]() ,
, ![]() is horizontal where
is horizontal where ![]() and
and ![]() , and the tangent is vertical where
, and the tangent is vertical where ![]() and
and ![]() .
.
Finding the Derivative for a Parametric Curve
For each of the following parametrically defined plane curves, calculate the derivative ![]() as well as determine the points, where the tangent line is horizontal and the points, where the tangent line is vertical.
as well as determine the points, where the tangent line is horizontal and the points, where the tangent line is vertical.
Solution
- To apply (*), first calculate
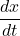 and
and 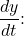
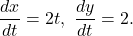
Next substitute these into (*):
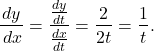
Since
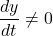 , there are no points on the curve, where the tangent line is horizontal. Solving
, there are no points on the curve, where the tangent line is horizontal. Solving 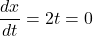 , we find the value of
, we find the value of 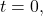 corresponding to the point on the curve, where the tangent line is vertical. Calculating
corresponding to the point on the curve, where the tangent line is vertical. Calculating 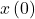 and
and 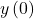 gives
gives 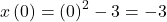 and
and 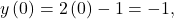 yielding the point
yielding the point 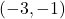 on the curve. Note that, eliminating the parameter, we can determine that this curve is a parabola opening to the right, and the point
on the curve. Note that, eliminating the parameter, we can determine that this curve is a parabola opening to the right, and the point 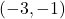 is its vertex as shown below.
is its vertex as shown below.
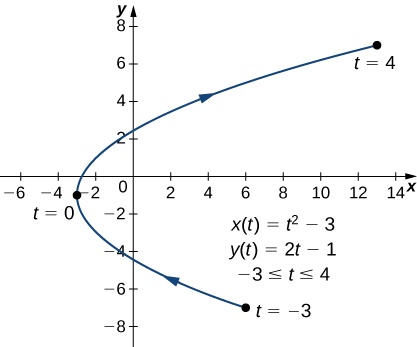
Figure 2. Graph of the parabola described by parametric equations in part a. - Again, we start by calculating
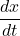 and
and 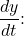
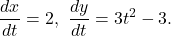
Next substitute these into (*) to find
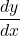 :
:
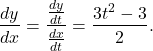
Since
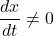 , there are no points on this curve, where the tangent line is vertical. To determine the points, where the tangent line is horizontal, we solve
, there are no points on this curve, where the tangent line is vertical. To determine the points, where the tangent line is horizontal, we solve 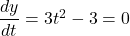 , and find that
, and find that 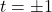 . When
. When 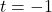 ,
, 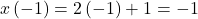 and
and 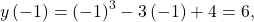 which corresponds to the point
which corresponds to the point 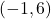 on the curve. When
on the curve. When 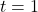 ,
,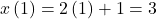 and
and 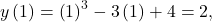 which corresponds to the point
which corresponds to the point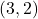 on the curve. The following figure provides the sketch of the curve.
on the curve. The following figure provides the sketch of the curve.
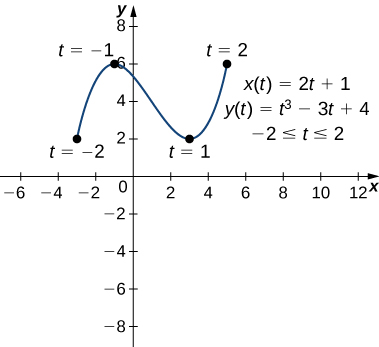
Figure 3. Graph of the curve described by parametric equations in part b. - Calculating
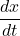 and
and 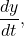 we obtain
we obtain
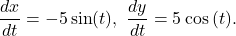
Therefore, (*) yields
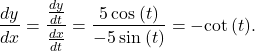
We see that
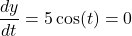 when
when 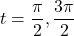 in the interval
in the interval ![Rendered by QuickLaTeX.com \ds[0,2\pi]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-0c6bb6eacbc7af9f38cfefea098cfe17_l3.png) . Note that
. Note that 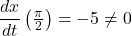 and
and 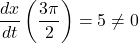 .
.Hence, each of these values of
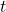 yields a point on the curve, where the tangent line is horizontal. To find the coordinates of these points, we substitute
yields a point on the curve, where the tangent line is horizontal. To find the coordinates of these points, we substitute 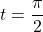 and
and 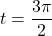 into
into 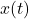 and
and 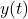 :
: 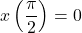 ,
, 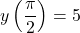 , yielding the point
, yielding the point 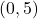 , and
, and 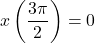 ,
, 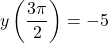 , yielding the point
, yielding the point 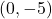 .
. Solving
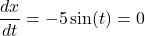 , we find
, we find 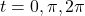 within
within ![Rendered by QuickLaTeX.com [0,2\pi]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-ce20c94fe55da7e7ed58648120072837_l3.png) . Since
. Since 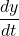 is non-zero at all these values of
is non-zero at all these values of 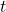 , each of them corresponds to a point on the curve, where the tangent line is vertical. Substituting
, each of them corresponds to a point on the curve, where the tangent line is vertical. Substituting 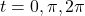 into
into 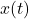 and
and 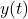 , we find the coordinates of these points to be
, we find the coordinates of these points to be 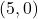 ,
, 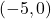 and
and 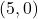 respectively.
respectively. The above computations agree with the sketch of the parametric curve, which is a circle of radius 5 with the center at the origin.
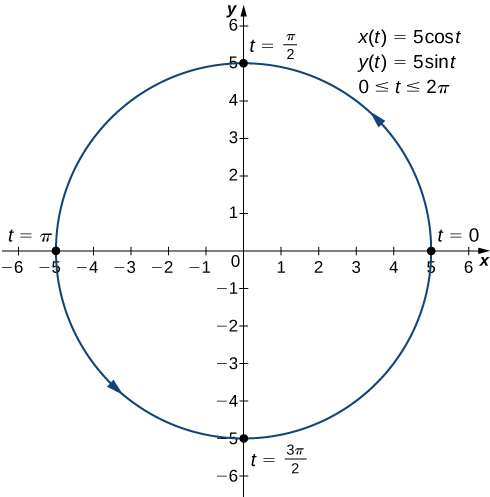
Figure 4. Graph of the curve described by parametric equations in part c.
Calculate the derivative ![]() for the curve defined by the parametric equations
for the curve defined by the parametric equations ![]()
![]() ,
, ![]() and find all points on the curve, where the tangent line is horizontal or where the tangent line is vertical.
and find all points on the curve, where the tangent line is horizontal or where the tangent line is vertical.
Answer
![]()
The tangent line line is horizontal at ![]() and
and ![]() , corresponding to
, corresponding to ![]() and
and ![]() respectively. The tangent line is vertical at
respectively. The tangent line is vertical at ![]() , corresponding to
, corresponding to ![]() .
.
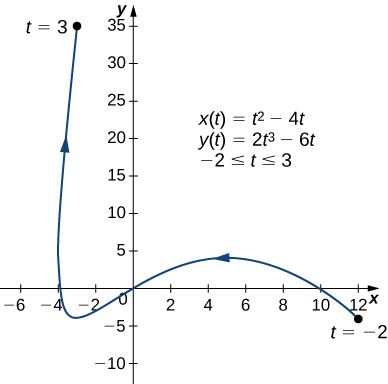
Slope of the Tangent Line in a Special Case
Determine the slope of the tangent line to the hypocycloid
![]()
Solution
We first calculate ![]() and
and ![]()
We see that ![]() , and so (*) cannot be applied to find
, and so (*) cannot be applied to find ![]() when
when ![]() . However,
. However, ![]() when
when ![]() ,
, ![]() , and so we can consider
, and so we can consider ![]() :
:
![]()
Since ![]() we deal with a
we deal with a ![]() indeterminate form and can apply L’Hospital’s rule.
indeterminate form and can apply L’Hospital’s rule.
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill \lim\limits_{t\to0} \dfrac{dy}{dx}&\ds =\hfill &\ds \lim\limits_{t\to0} \dfrac{3\cos(t)-3\cos(3t)}{-3\sin(t)-3\sin(3t)}\hfill \\[5mm]\ds \hfill &\ds =\hfill &\ds \lim\limits_{t\to0} \dfrac{-3\sin(t)+9\sin(3t)}{-3\cos(t)-9\cos(3t)}\hfill \\[5mm]\ds \hfill &\ds =\hfill &\ds \dfrac{-0+0}{-3-9}=\frac{0}{-12}=0.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-43d16cd120ab3e3ffa9cf556405dc0e5_l3.png)
Therefore, when ![]() , the slope of the tangent line is zero, and hence the tangent line to the hypocycloid is horizontal at the point
, the slope of the tangent line is zero, and hence the tangent line to the hypocycloid is horizontal at the point ![]() , corresponding to
, corresponding to ![]() , where the curve has a cusp.
, where the curve has a cusp.
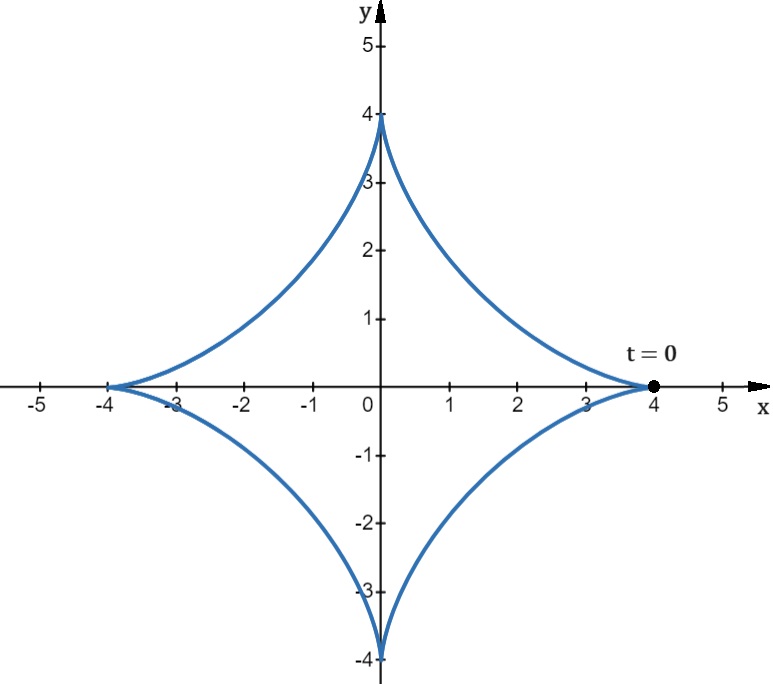
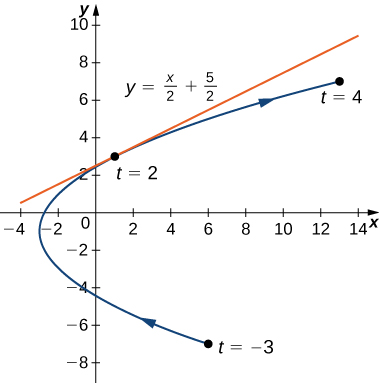
Finding a Tangent Line
Find the equation of the tangent line to the parametric curve defined by the equations
![]()
Solution
We first calculate ![]() and
and ![]()
Next we substitute these into (*):
![]()
When ![]()
![]() so this is the slope of the tangent line. Calculating
so this is the slope of the tangent line. Calculating ![]() and
and ![]() gives
gives ![]() and
and ![]() which corresponds to the point
which corresponds to the point ![]() on the curve, see Figure 5 below. We now use the point-slope form of the equation of a line to find the equation of the tangent line at this point:
on the curve, see Figure 5 below. We now use the point-slope form of the equation of a line to find the equation of the tangent line at this point:
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill y-{y}_{0}&\ds =\hfill &\ds m\left(x-{x}_{0}\right)\hfill \\[5mm]\ds \hfill y-3&\ds =\hfill &\ds \frac{1}{2}\left(x-1\right)\hfill \\[5mm]\ds \hfill y-3&\ds =\hfill &\ds \frac{1}{2}x-\frac{1}{2}\hfill \\[5mm]\ds \hfill y&\ds =\hfill &\ds \frac{1}{2}x+\frac{5}{2}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-13c3bba2efea03dec74b5fdaa106dfb0_l3.png)
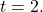
Find the equation of the tangent line to the curve defined by the equations
![]()
Answer
The equation of the tangent line is ![]()
Second-Order Derivatives
Our next goal is to see how to take the second derivative of a function defined parametrically. The second derivative of a function ![]() is defined to be the derivative of the first derivative; that is,
is defined to be the derivative of the first derivative; that is,
![]()
Since 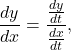 we can replace the
we can replace the ![]() on both sides of this equation with
on both sides of this equation with ![]() This gives us
This gives us
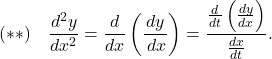
If we know ![]() as a function of t, then this formula is straightforward to apply.
as a function of t, then this formula is straightforward to apply.
Calculate the second derivative ![]() for the plane curve defined by the equations
for the plane curve defined by the equations
Answer
![]()
From before, we know that the second derivative is “responsible” for concavity of the curve with an explicit equation ![]() : the curve is concave upward where
: the curve is concave upward where ![]() , and it is concave downward where
, and it is concave downward where ![]() Since, locally, a parametric curve usually admits eliminating the parameter and obtaining an explicit equation, we can still look at the sign of
Since, locally, a parametric curve usually admits eliminating the parameter and obtaining an explicit equation, we can still look at the sign of ![]() , to determine where the curve is concave upward and where it is concave downward. Because, in practice, we won't be finding an explicit equation of the curve, but we will be using (**) to find
, to determine where the curve is concave upward and where it is concave downward. Because, in practice, we won't be finding an explicit equation of the curve, but we will be using (**) to find ![]() as a function of
as a function of ![]() , it is the intervals in terms of
, it is the intervals in terms of ![]() that we will be referring to when discussing concavity of parametric curves.
that we will be referring to when discussing concavity of parametric curves.
Examining Concavity of a Parametric Curve
Determine where the parametric curve ![]() ,
, ![]() is concave upward and where it is concave downward.
is concave upward and where it is concave downward.
Solution
Applying (*), we find that ![]() Using (**) together with the quotient rule, we obtain
Using (**) together with the quotient rule, we obtain
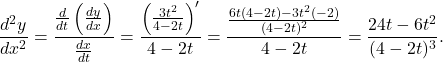
We now need to determine for which values of ![]() ,
, ![]() is positive, and for which values of
is positive, and for which values of ![]() it is negative. Factoring the numerator and denominator, we rewrite
it is negative. Factoring the numerator and denominator, we rewrite ![]() :
:
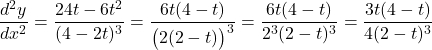 .
. The numerator has zeros ![]() and
and ![]() , while the denominator has a zero
, while the denominator has a zero ![]() of multiplicity 3. Using sample points or any other appropriate method, we find that
of multiplicity 3. Using sample points or any other appropriate method, we find that ![]() , and hence the parametric curve is concave upward, when
, and hence the parametric curve is concave upward, when ![]() and
and ![]() , and
, and ![]() , implying that the curve is concave downward, when
, implying that the curve is concave downward, when ![]() and
and ![]() .
.
Determine where the parametric curve ![]() ,
, ![]() is concave upward.
is concave upward.
Answer
The curve is concave upward when ![]() .
.
Integrals Involving Parametric Equations
Now that we have seen how to calculate the derivative of a plane curve, the next question is this: How do we find the area under a curve defined parametrically? Recall the cycloid defined by the equations ![]() Suppose we want to find the area of the shaded region in the following graph.
Suppose we want to find the area of the shaded region in the following graph.
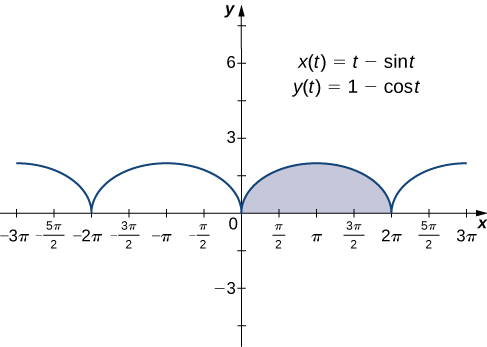
![Rendered by QuickLaTeX.com \ds \left[0,2\pi \right]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-d4c3e07b5e02fe7225629a67ce93c5d7_l3.png) highlighted.
highlighted.To derive a formula for the area under the curve defined by the functions
![]()
we assume that ![]() is increasing and differentiable and start with an equal partition of the interval
is increasing and differentiable and start with an equal partition of the interval ![]() Suppose
Suppose ![]() and consider the following graph.
and consider the following graph.
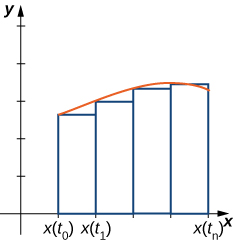
We use rectangles to approximate the area under the curve. The height of a typical rectangle in this parametrization is ![]() for some value
for some value ![]() in the ith subinterval, and the width can be calculated as
in the ith subinterval, and the width can be calculated as ![]() . It follows that the area of the ith rectangle is given by
. It follows that the area of the ith rectangle is given by
![]()
Then a Riemann sum for the area is
![]()
Multiplying and dividing each area by ![]() gives
gives
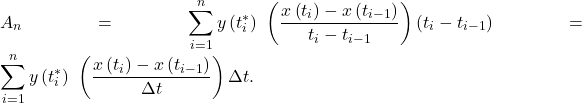
Taking the limit as ![]() approaches infinity, we obtain
approaches infinity, we obtain
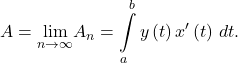
Note that if ![]() is decreasing, that is, the curve is traced from left to right, everything in the above derivation stays the same except that the width of a typical rectangle becomes
is decreasing, that is, the curve is traced from left to right, everything in the above derivation stays the same except that the width of a typical rectangle becomes ![]() , which results in the formula
, which results in the formula
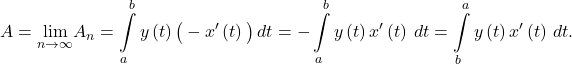
This leads to the following theorem.
Area under a Parametric Curve
Consider the plane curve defined by the parametric equations
![]()
and assume that ![]() is differentiable.
is differentiable.
- If
 is increasing, then the area under this curve is given by
is increasing, then the area under this curve is given by
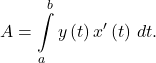
-
If
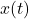 is decreasing, then the area under this curve is given by
is decreasing, then the area under this curve is given by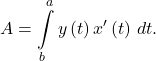
Finding the Area under a Parametric Curve
Find the area under one arc of the cycloid defined by the equations
Solution
To determine whether ![]() is increasing or decreasing we look at the sign of
is increasing or decreasing we look at the sign of ![]() . We have that
. We have that ![]() , and hence
, and hence ![]() is increasing. Applying the above theorem, we have
is increasing. Applying the above theorem, we have
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill A&\ds =\int\limits_{a}^{b}y\left(t\right){x}^{\prime }\left(t\right)\phantom{\rule{0.2em}{0ex}}dt\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{2\pi }\left(1-\text{cos}\phantom{\rule{0.2em}{0ex}}(t)\right)\left(1-\text{cos}\phantom{\rule{0.2em}{0ex}}(t)\right)\phantom{\rule{0.2em}{0ex}}dt\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{2\pi }\left(1-2\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(t)+{\text{cos}}^{2}(t)\right)dt\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{2\pi }\left(1-2\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(t)+\frac{1+\text{cos}\phantom{\rule{0.2em}{0ex}}(2t)}{2}\right)\phantom{\rule{0.2em}{0ex}}dt\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{2\pi }\left(\frac{3}{2}-2\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(t)+\frac{\text{cos}\phantom{\rule{0.2em}{0ex}}(2t)}{2}\right)\phantom{\rule{0.2em}{0ex}}dt\hfill \\[5mm]\ds &\ds =\left({\frac{3t}{2}-2\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(t)+\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}(2t)}{4}}\right)\Big|_{0}^{2\pi }\hfill \\[5mm]\ds &\ds =3\pi .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-fd7a50aa5dc4aaf55760761bda4f6160_l3.png)
Find the area under the upper half of the hypocycloid defined by the equations
Answer
![]()
Hint
Use the above theorem, along with the identities ![]() and
and ![]() Note that
Note that ![]() is decreasing.
is decreasing.
Arc Length of a Parametric Curve
The same way we did for a regular curve with explicit equation ![]() or
or ![]() , to derive a formula for the arc length of a parametric curve, we approximate it by a union of line segments as shown in the following figure.
, to derive a formula for the arc length of a parametric curve, we approximate it by a union of line segments as shown in the following figure.
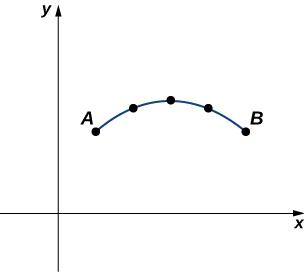
Given a plane curve defined by the parametric equations ![]() we start by partitioning the interval
we start by partitioning the interval ![]() into n equal subintervals:
into n equal subintervals: ![]() The width of each subinterval is
The width of each subinterval is ![]() The length of the
The length of the ![]() th line segment can be found as follows:
th line segment can be found as follows:
![]()
Adding those from ![]() , we obatin an approximation of the arc length s of the parametric curve:
, we obatin an approximation of the arc length s of the parametric curve:
![]()
If we assume that ![]() and
and ![]() are differentiable functions of t, then the Mean Value Theorem applies, so in each subinterval
are differentiable functions of t, then the Mean Value Theorem applies, so in each subinterval ![]() there exist
there exist ![]() and
and ![]() such that
such that
![Rendered by QuickLaTeX.com \ds \begin{array}{ll}\ds \ds \\[5mm]\ds x\left({t}_{i}\right)-x\left({t}_{i-1}\right)={x}^{\prime }\left(t^*_{i}\right)\left({t}_{i}-{t}_{i-1}\right)={x}^{\prime }\left(t^*_{i}\right)\Delta t\hfill \\[5mm]\ds y\left({t}_{i}\right)-y\left({t}_{i-1}\right)={y}^{\prime }\left(t^{**}_{i}\right)\left({t}_{i}-{t}_{i-1}\right)={y}^{\prime }\left(t^{**}_{i}\right)\Delta t.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-1ad76f63e6ab9591715ace0053e2eea2_l3.png)
With this, ![]() becomes
becomes
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill s&\ds \approx \sum _{i=1}^{n}{d}_{i}\hfill \\[5mm]\ds &\ds =\sum _{i=1}^{n}\sqrt{{\left({x}^{\prime }\left(t^*_{i}\right)\Delta t\right)}^{2}+{\left({y}^{\prime }\left(t^{**}_{i}\right)\Delta t\right)}^{2}}\hfill \\[5mm]\ds &\ds =\sum _{i=1}^{n}\sqrt{{\left({x}^{\prime }\left(t^*_{i}\right)\right)}^{2}{\left(\Delta t\right)}^{2}+{\left({y}^{\prime }\left(t^{**}_{i}\right)\right)}^{2}{\left(\Delta t\right)}^{2}}\hfill \\[5mm]\ds &\ds =\left(\sum _{i=1}^{n}\sqrt{{\left({x}^{\prime }\left(t^*_{i}\right)\right)}^{2}+{\left({y}^{\prime }\left(t^{**}_{i}\right)\right)}^{2}}\right)\Delta t.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-968704cb76b535ee4325b4705c568316_l3.png)
This is a Riemann sum that approximates the arc length over a partition of the interval ![]() If we further assume that the derivatives are continuous and let the number of points in the partition increase without bound, the approximation approaches the exact arc length. This gives
If we further assume that the derivatives are continuous and let the number of points in the partition increase without bound, the approximation approaches the exact arc length. This gives
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill s&\ds =\underset{n\to \infty }{\text{lim}}\sum _{i=1}^{n}{d}_{i}\hfill \\[5mm]\ds &\ds =\underset{n\to \infty }{\text{lim}}\left(\sum _{i=1}^{n}\sqrt{{\left({x}^{\prime }\left(t^*_{i}\right)\right)}^{2}+{\left({y}^{\prime }\left(t^{**}_{i}\right)\right)}^{2}}\right)\Delta t\hfill \\[5mm]\ds &\ds =\int\limits_{a}^{b}\sqrt{{\left({x}^{\prime }\left(t\right)\right)}^{2}+{\left({y}^{\prime }\left(t\right)\right)}^{2}}dt.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-90c281c219d9e11a0bb2103ab04898f1_l3.png)
When taking the limit, the values of ![]() and
and ![]() are both contained within the same ever-shrinking interval of width
are both contained within the same ever-shrinking interval of width ![]() so they must converge to the same value.
so they must converge to the same value.
We can summarize this method in the following theorem.
Arc Length of a Parametric Curve
Consider the plane curve defined by the parametric equations
![]()
and assume that ![]() and
and ![]() are smooth, that is, their derivatives
are smooth, that is, their derivatives ![]() and
and ![]() are continuous. Then the arc length of this curve is given by
are continuous. Then the arc length of this curve is given by
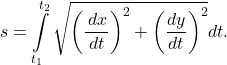
Now suppose that the parameter can be eliminated, leading to a function ![]() We are going to show that the above formula agrees with the formula for the arc length of a regular curve derived in Section 2.4. We have
We are going to show that the above formula agrees with the formula for the arc length of a regular curve derived in Section 2.4. We have ![]() and the Chain Rule gives
and the Chain Rule gives ![]() Substituting this into the above formula gives
Substituting this into the above formula gives
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill s&\ds =\int\limits_{{t}_{1}}^{{t}_{2}}\sqrt{{\left(\frac{\,dx }{dt}\right)}^{2}+{\left(\frac{dy}{dt}\right)}^{2}}dt\hfill \\[5mm]\ds &\ds =\int\limits_{{t}_{1}}^{{t}_{2}}\sqrt{{\left(\frac{\,dx }{dt}\right)}^{2}+{\left({F}^{\prime }\left(x\right)\frac{\,dx }{dt}\right)}^{2}}dt\hfill \\[5mm]\ds &\ds =\int\limits_{{t}_{1}}^{{t}_{2}}\sqrt{{\left(\frac{\,dx }{dt}\right)}^{2}\left(1+{\left({F}^{\prime }\left(x\right)\right)}^{2}\right)}dt\hfill \\[5mm]\ds &\ds =\int\limits_{{t}_{1}}^{{t}_{2}}{x}^{\prime }\left(t\right)\sqrt{1+{\left(\frac{dy}{\,dx }\right)}^{2}}dt.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-8f90bc1a730fcd62a944b9c9c52d471c_l3.png)
Here we have assumed that ![]() and the case when
and the case when ![]() is analogous (the extra minus is going to disappear when the limits of integration are interchanged). Using a substitution
is analogous (the extra minus is going to disappear when the limits of integration are interchanged). Using a substitution ![]() , we have that
, we have that ![]() and letting
and letting ![]() and
and ![]() we obtain the formula
we obtain the formula
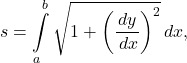
which is exactly the one we had before.
Finding the Arc Length of a Parametric Curve
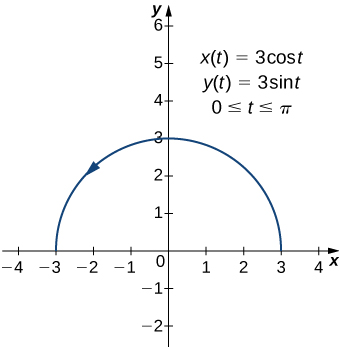
Find the arc length of the semicircle defined by the equations
Solution
The parametric curve is shown in Figure 9 below. To determine its length, we use the formula:
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill s&\ds =\int\limits_{{t}_{1}}^{{t}_{2}}\sqrt{{\left(\frac{\,dx }{dt}\right)}^{2}+{\left(\frac{dy}{dt}\right)}^{2}}dt\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{\pi }\sqrt{{\left(-3\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(t)\right)}^{2}+{\left(3\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(t)\right)}^{2}}dt\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{\pi }\sqrt{9\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{2}(t)+9\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{2}(t)}\phantom{\rule{0.2em}{0ex}}dt\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{\pi }\sqrt{9\left({\text{sin}}^{2}(t)+{\text{cos}}^{2}(t)\right)}dt\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{\pi }3dt={3t}\Big|_{0}^{\pi }=3\pi .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-0b5c5bcf2e7f606229c9576533e11acb_l3.png)
Note that the formula for the arc length of a semicircle is ![]() and the radius of this circle is 3. This is a great example of using calculus to derive a known geometric formula.
and the radius of this circle is 3. This is a great example of using calculus to derive a known geometric formula.
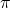
Find the arc length of the curve defined by the equations
Answer
![]()
We now return to the problem posed at the beginning of the section about a baseball leaving a pitcher’s hand. Ignoring the effect of air resistance (unless it is a curve ball!), the ball travels in a parabolic path. Assuming the pitcher’s hand is at the origin and the ball travels left to right in the direction of the positive x-axis, the parametric equations for this curve can be written as
![]()
where t represents time. We first calculate the distance the ball travels as a function of time. This distance is represented by the arc length. We can modify the arc length formula slightly. First rewrite the functions ![]() and
and ![]() using v as an independent variable, so as to eliminate any confusion with the parameter t:
using v as an independent variable, so as to eliminate any confusion with the parameter t:
![]()
Then we write the arc length formula as follows:
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill s\left(t\right)&\ds =\int\limits_{0}^{t}\sqrt{{\left(\frac{\,dx }{dv}\right)}^{2}+{\left(\frac{dy}{dv}\right)}^{2}}dv\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{t}\sqrt{{140}^{2}+{\left(-32v+2\right)}^{2}}dv.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7a0ac9adafacf11e7fadf3817a6f3c30_l3.png)
The variable v acts as a dummy variable that disappears after integration, leaving the arc length as a function of time t. To integrate this expression, one needs to make a trigonometric substitution ![]() , which will lead to a constant multiple of an integral of
, which will lead to a constant multiple of an integral of ![]() . After some technical computations, this will result in
. After some technical computations, this will result in
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill s\left(t\right)&\ds =-\frac{1}{32}\left[\frac{\left(-32t+2\right)}{2}\sqrt{{140}^{2}+{\left(-32t+2\right)}^{2}}+\frac{{140}^{2}}{2}\text{ln}|\left(-32t+2\right)+\sqrt{{140}^{2}+{\left(-32t+2\right)}^{2}}|\right]\hfill \\[5mm]\ds &\ds \phantom{\rule{0.6em}{0ex}}+\frac{1}{32}\left[\sqrt{{140}^{2}+{2}^{2}}+\frac{{140}^{2}}{2}\text{ln}|2+\sqrt{{140}^{2}+{2}^{2}}|\right]\hfill \\[5mm]\ds &\ds =\left(\frac{t}{2}-\frac{1}{32}\right)\sqrt{1024{t}^{2}-128t+19604}-\frac{1225}{4}\text{ln}|\left(-32t+2\right)+\sqrt{1024{t}^{2}-128t+19604}|\hfill \\[5mm]\ds &\ds \phantom{\rule{0.6em}{0ex}}+\frac{\sqrt{19604}}{32}+\frac{1225}{4}\text{ln}\left(2+\sqrt{19604}\right).\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-0ca33cc90cdbc0934838f078a1d78294_l3.png)
This function represents the distance traveled by the ball as a function of time. To calculate the speed, take the derivative of this function with respect to t. While this may seem like a daunting task, it is possible to obtain the answer directly from the Fundamental Theorem of Calculus:
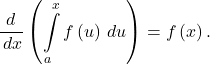 Therefore,
Therefore,
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill {s}^{\prime }\left(t\right)&\ds =\frac{d}{dt}\left[s\left(t\right)\right]\hfill \\[5mm]\ds &\ds =\frac{d}{dt}\left[\int\limits_{0}^{t}\sqrt{{140}^{2}+{\left(-32v+2\right)}^{2}}dv\right]\hfill \\[5mm]\ds &\ds =\sqrt{{140}^{2}+{\left(-32t+2\right)}^{2}}\hfill \\[5mm]\ds &\ds =\sqrt{1024{t}^{2}-128t+19604}\hfill \\[5mm]\ds &\ds =2\sqrt{256{t}^{2}-32t+4901}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-0e2392d23ef312fd9d7075a0c0c3b65e_l3.png)
One third of a second after the ball leaves the pitcher’s hand, the distance it travels is equal to
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill s\left(\frac{1}{3}\right)&\ds =\left(\frac{1\text{/}3}{2}-\frac{1}{32}\right)\sqrt{1024{\left(\frac{1}{3}\right)}^{2}-128\left(\frac{1}{3}\right)+19604}\hfill \\[5mm]\ds &\ds \phantom{\rule{0.6em}{0ex}}-\frac{1225}{4}\text{ln}|\left(-32\left(\frac{1}{3}\right)+2\right)+\sqrt{1024{\left(\frac{1}{3}\right)}^{2}-128\left(\frac{1}{3}\right)+19604}|\hfill \\[5mm]\ds &\ds \phantom{\rule{0.6em}{0ex}}+\frac{\sqrt{19604}}{32}+\frac{1225}{4}\text{ln}\left(2+\sqrt{19604}\right)\hfill \\[5mm]\ds &\ds \approx 46.69\phantom{\rule{0.2em}{0ex}}\text{feet}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-a2d1c33796c4046ee7ac9cb0e799a4d2_l3.png)
This value is just over three quarters of the way to home plate. The speed of the ball is
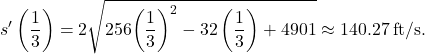
This speed translates to approximately 95 mph—a major-league fastball.
Surface Area Generated by a Parametric Curve
Recall the problem of finding the surface area of a surface of revolution. In Section 2.4, we derived a formula for the surface area of a surface generated by revolving the curve ![]() from
from ![]() to
to ![]() around the x-axis:
around the x-axis:
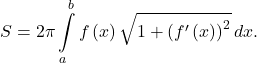
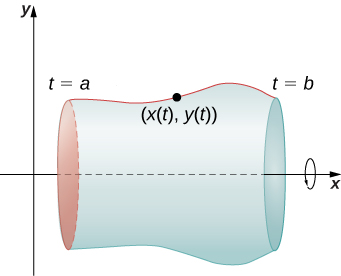
We now consider a surface of revolution generated by revolving a parametrically defined curve ![]() around the x-axis as shown in the following figure.
around the x-axis as shown in the following figure.
The formula for its surface area is
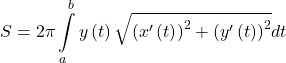
provided that ![]() is non-negative on
is non-negative on ![]()
Finding Surface Area
Find the surface area of a sphere of radius r centered at the origin.
Solution
We start by parametrizing the upper semicircle with center at the origin and radius ![]() :
:
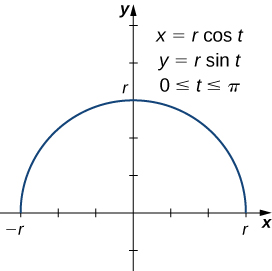
When this curve is revolved around the x-axis, it generates a sphere of radius r. To calculate the surface area of the sphere, we use the above formula:
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill S&\ds =2\pi \int\limits_{a}^{b}y\left(t\right)\sqrt{{\left({x}^{\prime }\left(t\right)\right)}^{2}+{\left({y}^{\prime }\left(t\right)\right)}^{2}}dt\hfill \\[5mm]\ds &\ds =2\pi \int\limits_{0}^{\pi }r\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(t)\sqrt{{\left( - r\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(t)\right)}^{2}+{\left(r\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(t)\right)}^{2}}dt\hfill \\[5mm]\ds &\ds =2\pi \int\limits_{0}^{\pi }r\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(t)\sqrt{{r}^{2}{\text{sin}}^{2}(t)+{r}^{2}{\text{cos}}^{2}(t)}\phantom{\rule{0.2em}{0ex}}dt\hfill \\[5mm]\ds &\ds =2\pi \int\limits_{0}^{\pi }r\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(t)\sqrt{{r}^{2}\left({\text{sin}}^{2}(t)+{\text{cos}}^{2}(t)\right)}dt\hfill \\[5mm]\ds &\ds =2\pi \int\limits_{0}^{\pi }{r}^{2}\text{sin}\phantom{\rule{0.2em}{0ex}}(t)\phantom{\rule{0.2em}{0ex}}dt\hfill \\[5mm]\ds &\ds =2\pi {r}^{2}\left({ - \text{cos}\phantom{\rule{0.2em}{0ex}}(t)}\Big|_{0}^{\pi }\right)\hfill \\[5mm]\ds &\ds =2\pi {r}^{2}\left( - \text{cos}\phantom{\rule{0.2em}{0ex}}\pi +\text{cos}\phantom{\rule{0.2em}{0ex}}0\right)\hfill \\[5mm]\ds &\ds =4\pi {r}^{2}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-1493b1bdcb0bc94729213f320f208e0a_l3.png)
This agrees with the geometric you might have seen before.
Find the area of the surface generated by revolving the plane curve defined by the equations
![]()
around the x-axis.
Answer
![]()
Hint
When evaluating the integral, use a u-substitution.
Key Concepts
- The derivative of the parametrically defined curve
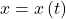 and
and 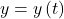 can be calculated using the formula
can be calculated using the formula 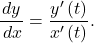 Using the derivative, we can find the equation of a tangent line to a parametric curve.
Using the derivative, we can find the equation of a tangent line to a parametric curve. - If
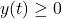 , the area under the parametric curve can be determined by using the formula
, the area under the parametric curve can be determined by using the formula 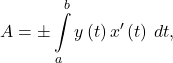 where the choice of sign depends on whether
where the choice of sign depends on whether  is increasing or decreasing over
is increasing or decreasing over ![Rendered by QuickLaTeX.com [a,b]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-2ba33d54179d658fa4d4f6a34c15cb9f_l3.png) .
. - The arc length of a parametric curve can be calculated by using the formula
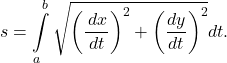
- The area of a surface obtained by revolving a parametric curve around the x-axis is given by
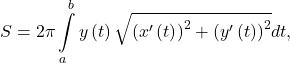 provided
provided 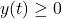 when
when ![Rendered by QuickLaTeX.com t\in[a,b]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-3c3dd904a72533b2f86965b6b5c2211b_l3.png) . If the curve is revolved around the y-axis, then the formula is
. If the curve is revolved around the y-axis, then the formula is 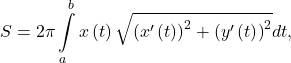
provided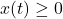 when
when ![Rendered by QuickLaTeX.com t\in[a,b]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-3c3dd904a72533b2f86965b6b5c2211b_l3.png) .
.
Key Equations
- Derivative of parametric equations
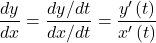
- Second-order derivative of parametric equations
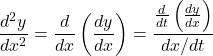
- Area under a parametric curve
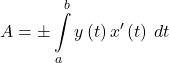 , where the sign depends on the sign of
, where the sign depends on the sign of 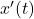
- Arc length of a parametric curve
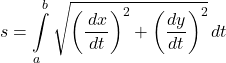
- Surface area generated by a parametric curve about a coordinate axis
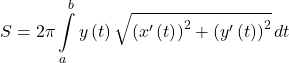 (revolving about x-axis)
(revolving about x-axis)
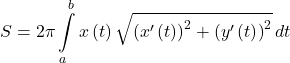 (revolving about y-axis)
(revolving about y-axis)
Exercises
For the following exercises, find ![]() as a function of the parameter t.
as a function of the parameter t.
1. ![]()
Answer
![]()
2. ![]()
3. ![]()
Answer
![]()
4. ![]()
For the following exercises, each set of parametric equations represents a line. Without eliminating the parameter, find the slope of each line.
5. ![]()
Answer
![]()
6. ![]()
7. ![]()
Answer
0
For the following exercises, determine the slope of the tangent line at the point corresponding to the given value of the parameter.
8. ![]()
9. ![]()
Answer
![]()
10. ![]()
11. ![]()
Answer
Slope is undefined.
12. ![]()
For the following exercises, find all points on the parametric curve where the tangent line has the given slope.
13. ![]()
Answer
![]() , where
, where ![]() is integer, corresponding to the points
is integer, corresponding to the points ![]() and
and ![]() .
.
14. ![]()
15. ![]()
Answer
![]() corresponding to the point
corresponding to the point ![]() (note that
(note that ![]() is not in the domain of
is not in the domain of ![]() )
)
16. ![]()
For the following exercises, write an equation of the tangent line to the given parametric curve at the point that corresponds to the specified value of the parameter t.
17. ![]()
Answer
![]()
18. ![]()
19. ![]()
Answer
![]()
20. Consider the parametric curve ![]() Find all values of the parameter
Find all values of the parameter ![]() that correpsond to the points on the curve where the tangent line is horizontal.
that correpsond to the points on the curve where the tangent line is horizontal.
21. Consider the parametric curve ![]()
![]() Find all values of the parameter
Find all values of the parameter ![]() that correpsond to the points on the curve where the tangent line is vertical.
that correpsond to the points on the curve where the tangent line is vertical.
Answer
![]() .
.
For the following exercises, find all points on the given parametric curve where the tangent line is horizontal or vertical.
22. ![]()
23. ![]()
Answer
No horizontal tangents. Vertical tangents at ![]()
24. ![]()
25. ![]()
Answer
Horizontal tangent at ![]() vertical tangents at
vertical tangents at ![]()
For the following exercises, find ![]()
26. ![]()
27. ![]()
Answer
![]()
28. ![]()
29. ![]()
Answer
![]()
For the following exercises, find ![]() at the specified value of the parameter.
at the specified value of the parameter.
30. ![]()
31. ![]()
Answer
4
For the following exercises, find t intervals on which the given parametric curve is concave up and t intervals on which it is concave down.
32. ![]()
33. ![]()
Answer
Concave up on ![]()
34. ![]()
35. ![]()
Answer
Concave up on ![]() and concave down on
and concave down on ![]() .
.
36. Sketch and find the area under one arch of the cycloid ![]() Here
Here ![]() is a fixed real number and
is a fixed real number and ![]() is a parameter.
is a parameter.
37. Find the area below the curve ![]() and above the x-axis.
and above the x-axis.
Answer
2
38. Find the area enclosed by the ellipse ![]()
39. Find the area of the region below the curve ![]() and above the x-axis over the interval
and above the x-axis over the interval ![]()
Answer
![]()
For the following exercises, find the total area of the regions between the parametric curves and the x-axis. In exercises 41-43 ![]() is a fixed real number.
is a fixed real number.
40. ![]()
41.* ![]() .
.
Answer
![]()
42. ![]() (the “hourglass”)
(the “hourglass”)
43.[T] ![]() (the “teardrop”)
(the “teardrop”)
Answer
![]()
For the following exercises, find the arc length of the given parametric curve.
44. ![]()
45. ![]()
Answer
![]()
46. ![]()
47. ![]()
Answer
![]()
48. ![]()
49. ![]() (the hypocycloid)
(the hypocycloid)
Answer
![]()
50. Find the length of one arch of the cycloid ![]()
51. Find the distance traveled by a particle with position ![]() as t varies in the given time interval:
as t varies in the given time interval: ![]()
Answer
![]()
52. Find the length of the curve ![]()
For the following exercises, set up but do not evaluate the integral that represents the area of the surface obtained by rotating the given parametric curve about the x-axis.
53. ![]()
Answer
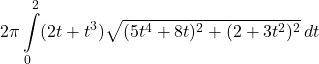
54. ![]()
55. ![]()
Answer
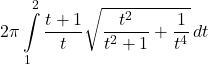
56. ![]()
For the following exercises, find the area of the surface obtained by rotating the given parametric curve about the x-axis.
57. ![]()
Answer
![]()
58. ![]()
For the following exercises, set up but do not evaluate the integral that represents the area of the surface obtained by rotating the given parametric curve about the y-axis.
59. ![]()
Answer
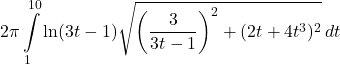
60. ![]()
61. Find the area of the surface generated by revolving ![]() about the y-axis.
about the y-axis.
Answer
![]()