2.4 Arc Length of a Curve and Surface Area
Learning Objectives
- Determine the length of a curve with equation
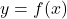 between the two given points.
between the two given points. - Determine the length of a curve with equation
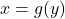 between the two given points.
between the two given points. - Find the surface area of a surface of revolution.
In this section, we use definite integrals to find the arc length of a curve. We can think of arc length as the distance you would travel if you were walking along the path of the curve. Many real-world applications involve arc length. If a rocket is launched along a parabolic path, we might want to know how far the rocket travels. Or, if a curve on a map represents a road, we might want to know how far we have to drive to reach our destination.
We begin by calculating the arc length of curves defined as functions of ![]() then we examine the same process for curves defined as functions of
then we examine the same process for curves defined as functions of ![]() (The process is identical, with the roles of
(The process is identical, with the roles of ![]() and
and ![]() reversed.) The techniques we use to find arc length can be extended to find the surface area of a surface of revolution, and we close the section with an examination of this concept.
reversed.) The techniques we use to find arc length can be extended to find the surface area of a surface of revolution, and we close the section with an examination of this concept.
Arc Length of the Curve y=f(x)
In previous applications of integration, we required the function ![]() to be integrable, or at most continuous. However, for calculating arc length we have a more stringent requirement for
to be integrable, or at most continuous. However, for calculating arc length we have a more stringent requirement for ![]() Here, we require
Here, we require ![]() to be differentiable, and furthermore we require its derivative,
to be differentiable, and furthermore we require its derivative, ![]() to be continuous. Functions like this, which have continuous derivatives, are called smooth . (This property comes up again in later chapters.)
to be continuous. Functions like this, which have continuous derivatives, are called smooth . (This property comes up again in later chapters.)
Let ![]() be a smooth function defined over
be a smooth function defined over ![]() We want to calculate the length of the curve from the point
We want to calculate the length of the curve from the point ![]() to the point
to the point ![]() We start by using line segments to approximate the length of the curve. For
We start by using line segments to approximate the length of the curve. For ![]() let
let ![]() be a regular partition of
be a regular partition of ![]() Then, for
Then, for ![]() construct a line segment from the point
construct a line segment from the point ![]() to the point
to the point ![]() Although it might seem logical to use either horizontal or vertical line segments, we want our line segments to approximate the curve as closely as possible. Figure 1 below depicts this construction for
Although it might seem logical to use either horizontal or vertical line segments, we want our line segments to approximate the curve as closely as possible. Figure 1 below depicts this construction for ![]()

To help us find the length of each line segment, we look at the change in vertical distance as well as the change in horizontal distance over each interval. Because we have used a regular partition, the change in horizontal distance over each interval is given by ![]() The change in vertical distance varies from interval to interval, though, so we use
The change in vertical distance varies from interval to interval, though, so we use ![]() to represent the change in vertical distance over the interval
to represent the change in vertical distance over the interval ![]() as shown in Figure 2 below. Note that some (or all)
as shown in Figure 2 below. Note that some (or all) ![]() may be negative.
may be negative.

![Rendered by QuickLaTeX.com \ds \left[{x}_{i-1},{x}_{i}\right].](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-147232e3e63c54f80b60dc5ea53a1578_l3.png)
By the Pythagorean theorem, the length of the line segment is ![]() We can also write this as
We can also write this as 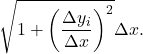 Now, by the Mean Value Theorem, there is a point
Now, by the Mean Value Theorem, there is a point ![]() such that
such that ![]() Then the length of the line segment is given by
Then the length of the line segment is given by ![]() Adding up the lengths of all the line segments, we get
Adding up the lengths of all the line segments, we get
![]()
This is a Riemann sum. Taking the limit as ![]() we have
we have
![Rendered by QuickLaTeX.com \ds \text{Arc Length}=\underset{n\to \infty }{\text{lim}}\underset{i=1}{\overset{n}{\sum}}\sqrt{1+{\left[{f}^{\prime }({x}_{i}^{*})\right]}^{2}}\Delta x=\int\limits_{a}^{b}\sqrt{1+{\left[{f}^{\prime }(x)\right]}^{2}}\,dx .](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-c4738f49bc60b752d81664f8e27e0cbc_l3.png)
We summarize these findings in the following theorem.
Arc Length for y=f(x)
Let ![]() be a smooth function over the interval
be a smooth function over the interval ![]() Then the arc length of the portion of the graph of
Then the arc length of the portion of the graph of ![]() from the point
from the point ![]() to the point
to the point ![]() is given by
is given by
![Rendered by QuickLaTeX.com \ds \text{Arc Length}=\int\limits_{a}^{b}\sqrt{1+{\left[{f}^{\prime }(x)\right]}^{2}}\,dx .](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-15baab2cf0616fc11f8a637096d0957c_l3.png)
Note that we are integrating an expression involving ![]() so we need to be sure
so we need to be sure ![]() is integrable. This is why we require
is integrable. This is why we require ![]() to be smooth. The following example shows how to apply the theorem.
to be smooth. The following example shows how to apply the theorem.
Calculating the Arc Length of a Function of x
Let ![]() Calculate the arc length of the graph of
Calculate the arc length of the graph of ![]() over the interval
over the interval ![]()
Solution
We have ![]() so
so ![]() Then, the arc length is
Then, the arc length is
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill \text{Arc Length}&\ds =\int\limits_{a}^{b}\sqrt{1+{\left[{f}^{\prime }(x)\right]}^{2}}\,dx \hfill \\[5mm]\ds &\ds =\int\limits_{0}^{1}\sqrt{1+9x}\,dx .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-3fede49f295174327d3911f27362d6f7_l3.png)
Substitute ![]() Then,
Then, ![]() When
When ![]() then
then ![]() and when
and when ![]() then
then ![]() Thus,
Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill \text{Arc Length}&\ds =\int\limits_{0}^{1}\sqrt{1+9x}\,dx \hfill \\[5mm]\ds &\ds =\frac{1}{9}\int\limits_{0}^{1}\sqrt{1+9x}\cdot 9\,\,dx =\frac{1}{9}\int\limits_{1}^{10}\sqrt{u}\,du\hfill \\[7mm]\ds &\ds ={\frac{1}{9}\cdot\frac{2}{3}{u}^{3\text{/}2}}\Big|_{1}^{10}=\frac{2}{27}\left[10\sqrt{10}-1\right]\text{units}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-8b1f4d62d3c3c70d7e981ad1e25f5ecd_l3.png)
Let ![]() Calculate the arc length of the graph of
Calculate the arc length of the graph of ![]() over the interval
over the interval ![]()
Answer
![]()
Although it is nice to have a formula for calculating arc length, this particular theorem can generate expressions that are difficult to integrate. We study some techniques for integration in the subsequent chapters of this text. Before we know them, we may have to stop after setting up the integral.
Setting Up the Integral for the Arc Length of a Function of x
Let ![]() Set up the integral for the arc length of the graph of
Set up the integral for the arc length of the graph of ![]() over the interval
over the interval ![]()
Solution
We have ![]() so
so ![]() Then the arc length is given by
Then the arc length is given by
![Rendered by QuickLaTeX.com \ds \text{Arc Length}=\int\limits_{a}^{b}\sqrt{1+{\left[{f}^{\prime }(x)\right]}^{2}}\,dx =\int\limits_{1}^{3}\sqrt{1+4{x}^{2}}\,dx .](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-cec40f0ad61d4ffec6921328d7775811_l3.png)
Let ![]() Set up the integral for the arc length of the graph of
Set up the integral for the arc length of the graph of ![]() over the interval
over the interval ![]()
Answer
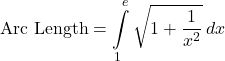
Hint
Use the process from the previous example.
Arc Length of the Curve x=g(y)
We have just seen how to approximate the length of a curve with line segments. If we want to find the arc length of the graph of a function of ![]() we can repeat the same process, except we partition the y-axis instead of the x-axis. Figure 3 below shows a representative line segment.
we can repeat the same process, except we partition the y-axis instead of the x-axis. Figure 3 below shows a representative line segment.

![Rendered by QuickLaTeX.com \ds \left[{y}_{i-1},{y}_{i}\right].](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-cef848f5977244ddbace9afa133b732a_l3.png)
Then the length of the line segment is ![]() which can also be written as
which can also be written as 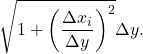 If we now follow the analogous steps to what we have done before, we get a formula for arc length of a function
If we now follow the analogous steps to what we have done before, we get a formula for arc length of a function ![]()
Arc Length for x=g(y)
Let ![]() be a smooth function over an interval
be a smooth function over an interval ![]() Then, the arc length of the graph of
Then, the arc length of the graph of ![]() from the point
from the point ![]() to the point
to the point ![]() is given by
is given by
![Rendered by QuickLaTeX.com \ds \text{Arc Length}=\int\limits_{c}^{d}\sqrt{1+{\left[{g}^{\prime }(y)\right]}^{2}}dy.](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-79810d821b27d2d705cacd2b4597ec47_l3.png)
Setting up the Integral for the Arc Length of a Function of y
Let ![]() Set up the integral for the arc length of the graph of
Set up the integral for the arc length of the graph of ![]() over the interval
over the interval ![]()
Solution
We have ![]() so
so ![]() Then the arc length is
Then the arc length is
![Rendered by QuickLaTeX.com \ds \text{Arc Length}=\int\limits_{c}^{d}\sqrt{1+{\left[{g}^{\prime }(y)\right]}^{2}}dy=\int\limits_{1}^{2}\sqrt{1+81{y}^{4}}\,dy.](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-ec0adc814f1ba9d47999e5d4eafc6e52_l3.png)
Let ![]() Set up the integral for the arc length of the graph of
Set up the integral for the arc length of the graph of ![]() over the interval
over the interval ![]()
Answer
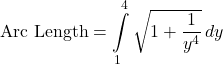
Hint
Use the process from the previous example.
Area of a Surface of Revolution
The concepts we used to find the arc length of a curve can be extended to find the surface area of a surface of revolution. Surface area is the total area of the outer layer of an object. For objects such as cubes or bricks, the surface area of the object is the sum of the areas of all of its faces. For curved surfaces, the situation is a little more complex. Let ![]() be a nonnegative smooth function over the interval
be a nonnegative smooth function over the interval ![]() We wish to find the surface area of the surface of revolution created by revolving the graph of
We wish to find the surface area of the surface of revolution created by revolving the graph of ![]() around the x-axis as shown in the following figure.
around the x-axis as shown in the following figure.

 (b) The surface of revolution formed by revolving the graph of
(b) The surface of revolution formed by revolving the graph of  around the x-axis.
around the x-axis.As we have done many times before, we are going to partition the interval ![]() and approximate the surface area by surface areas of simpler shapes. We start by using line segments to approximate the curve, as we did earlier in this section. For
and approximate the surface area by surface areas of simpler shapes. We start by using line segments to approximate the curve, as we did earlier in this section. For ![]() let
let ![]() be a regular partition of
be a regular partition of ![]() Then, for
Then, for ![]() construct a line segment from the point
construct a line segment from the point ![]() to the point
to the point ![]() Now, revolve these line segments around the x-axis to generate an approximation of the surface of revolution as shown in the following figure.
Now, revolve these line segments around the x-axis to generate an approximation of the surface of revolution as shown in the following figure.

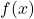 with line segments. (b) The surface of revolution formed by revolving the line segments around the x-axis.
with line segments. (b) The surface of revolution formed by revolving the line segments around the x-axis.Notice that when each line segment is revolved around the axis, it produces a band. These bands are actually pieces of cones (think of an ice cream cone with the pointy end cut off). A piece of a cone like this is called a frustum of a cone.
To find the surface area of the band, we need to find the lateral surface area, ![]() of the frustum (the area of just the slanted outside surface of the frustum, not including the areas of the top or bottom faces). Let
of the frustum (the area of just the slanted outside surface of the frustum, not including the areas of the top or bottom faces). Let ![]() and
and ![]() be the radii of the wide end and the narrow end of the frustum, respectively, and let
be the radii of the wide end and the narrow end of the frustum, respectively, and let ![]() be the slant height of the frustum as shown in the following figure.
be the slant height of the frustum as shown in the following figure.

We know the lateral surface area of a cone is given by
where ![]() is the radius of the base of the cone and
is the radius of the base of the cone and ![]() is the slant height (see the following figure).
is the slant height (see the following figure).

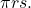
Since a frustum can be thought of as a piece of a cone, the lateral surface area of the frustum is given by the lateral surface area of the whole cone less the lateral surface area of the smaller cone (the pointy tip) that was cut off (see the following figure).

The cross-sections of the small cone and the large cone are similar triangles, so we see that
![]()
Solving for ![]() we get
we get
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill \ds\frac{{r}_{2}}{{r}_{1}}&\ds =\hfill &\ds \frac{s-l}{s}\hfill \\[5mm]\ds \hfill {r}_{2}s&\ds =\hfill &\ds {r}_{1}(s-l)\hfill \\[5mm]\ds \hfill {r}_{2}s&\ds =\hfill &\ds {r}_{1}s-{r}_{1}l\hfill \\[5mm]\ds \hfill {r}_{1}l&\ds =\hfill &\ds {r}_{1}s-{r}_{2}s\hfill \\[5mm]\ds \hfill {r}_{1}l&\ds =\hfill &\ds ({r}_{1}-{r}_{2})s\hfill \\[5mm]\ds \hfill s&\ds =\hfill &\ds \frac{{r}_{1}l}{{r}_{1}-{r}_{2}}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7e9e4b34762b30bdfd8e1940b93034fb_l3.png)
Then the lateral surface area (SA) of the frustum is
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill S&\ds =\text{(Lateral SA of large cone)}-\text{(Lateral SA of small cone)}\hfill \\[5mm]\ds &\ds =\pi {r}_{1}s-\pi {r}_{2}(s-l)\hfill \\[5mm]\ds &\ds =\pi {r}_{1}\left(\frac{{r}_{1}l}{{r}_{1}-{r}_{2}}\right)-\pi {r}_{2}\left(\frac{{r}_{1}l}{{r}_{1}-{r}_{2}}-l\right)\hfill \\[5mm]\ds &\ds =\frac{\pi {r}_{1}^{2}l}{{r}_{1}-{r}_{2}}-\frac{\pi {r}_{1}{r}_{2}l}{{r}_{1}-{r}_{2}}+\pi {r}_{2}l\hfill \\[5mm]\ds &\ds =\frac{\pi {r}_{1}^{2}l}{{r}_{1}-{r}_{2}}-\frac{\pi {r}_{1}{r}_{2}l}{{r}_{1}-{r}_{2}}+\frac{\pi {r}_{2}l({r}_{1}-{r}_{2})}{{r}_{1}-{r}_{2}}\hfill \\[5mm]\ds &\ds =\frac{\pi {r}_{1}^{2}l}{{r}_{1}-{r}_{2}}-\frac{\pi {r}_{1}{r}_{2}l}{{r}_{1}-{r}_{2}}+\frac{\pi {r}_{1}{r}_{2}l}{{r}_{1}-{r}_{2}}-\frac{\pi {r}_{2}{}^{2}l}{{r}_{1}-{r}_{2}}\hfill \\[5mm]\ds &\ds =\frac{\pi ({r}_{1}^{2}-{r}_{2}^{2})l}{{r}_{1}-{r}_{2}}=\frac{\pi ({r}_{1}-{r}_{2})({r}_{1}+{r}_{2})l}{{r}_{1}-{r}_{2}}=\pi ({r}_{1}+{r}_{2})l.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-845af5cf6c75c4feaf2399c6511e1392_l3.png)
Let’s now use this formula to calculate the surface area of each of the bands formed by revolving the line segments around the x-axis. A representative band is shown in the following figure.

Note that the slant height of this frustum is just the length of the line segment used to generate it. So, applying the surface area formula, we have
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill S&\ds =\pi ({r}_{1}+{r}_{2})l\hfill \\[5mm]\ds &\ds =\pi (f({x}_{i-1})+f({x}_{i}))\sqrt{(\Delta {x})^{2}+{(\Delta {y}_{i})}^{2}}\hfill \\[5mm]\ds &\ds =\pi (f({x}_{i-1})+f({x}_{i}))\sqrt{1+{\left(\frac{\Delta {y}_{i}}{\Delta x}\right)}^{2}}\Delta x.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-5371020594487abaaaf263019a3058a4_l3.png)
Now, as we did in the development of the arc length formula, we apply the Mean Value Theorem to select ![]() such that
such that ![]() This gives us
This gives us
![]()
Furthermore, since ![]() is continuous, by the Intermediate Value Theorem, there is a point
is continuous, by the Intermediate Value Theorem, there is a point ![]() such that
such that ![]() so we get
so we get
![]()
Then the approximate surface area of the whole surface of revolution is given by
![]()
This almost looks like a Riemann sum, except we have functions evaluated at two different points, ![]() and
and ![]() over the interval
over the interval ![]() Although we do not examine the details here, it turns out that because
Although we do not examine the details here, it turns out that because ![]() is smooth, if we let
is smooth, if we let ![]() the limit works the same as a Riemann sum even with the two different evaluation points. This makes sense intuitively. Both
the limit works the same as a Riemann sum even with the two different evaluation points. This makes sense intuitively. Both ![]() and
and ![]() are in the interval
are in the interval ![]() so it makes sense that as
so it makes sense that as ![]() both
both ![]() and
and ![]() approach
approach ![]() Those of you who are interested in the details should consult an advanced calculus text.
Those of you who are interested in the details should consult an advanced calculus text.
Taking the limit as ![]() we get
we get
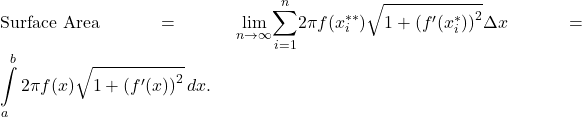
Let us now consider the surface obtained by rotating the same curve ![]() about the
about the ![]() -axis assuming that
-axis assuming that ![]() to ensure that the curve is on one side of the axis of revolution. We can still use the approach as above, approximating the sought surface area with the sum of surface areas of the bands, it’s only that now the frustum bands are going to be formed by rotating the line segment connecting the points
to ensure that the curve is on one side of the axis of revolution. We can still use the approach as above, approximating the sought surface area with the sum of surface areas of the bands, it’s only that now the frustum bands are going to be formed by rotating the line segment connecting the points ![]() and
and ![]() on the curve about the
on the curve about the ![]() -axis. This means that the parameters of the frustum are going to be
-axis. This means that the parameters of the frustum are going to be ![]() ,
, ![]() , while
, while ![]() remains the same. Therefore, we get
remains the same. Therefore, we get
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill S&\ds =\pi ({r}_{1}+{r}_{2})l\hfill \\[5mm]\ds &\ds =\pi ({x}_{i-1}+{x}_{i})\sqrt{(\Delta {x})^{2}+{(\Delta {y}_{i})}^{2}}\hfill \\[5mm]\ds &\ds =\pi ({x}_{i-1}+{x}_{i})\sqrt{1+{\left(\frac{\Delta {y}_{i}}{\Delta x}\right)}^{2}}\Delta x\hfill\\[5mm]\ds &\ds =2\pi \bar{x}_i\sqrt{1+{\left(f(x_i^*)\right)}^{2}}\Delta x,\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-f37fa6550127261a22b0964c3f90cc8f_l3.png)
where ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() comes from the application of the Mean Value Theorem, as before. Analogously, to what we’ve done above, we then obtain
comes from the application of the Mean Value Theorem, as before. Analogously, to what we’ve done above, we then obtain
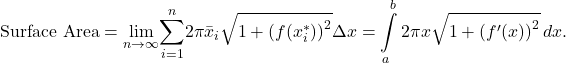
As with the arc length, we can now use a similar approach to derive formulas for the areas of surfaces obtained by revolving a curve with equation ![]() about the
about the ![]() and
and ![]() -axes. These findings are summarized in the following theorem.
-axes. These findings are summarized in the following theorem.
Surface Area of a Surface of Revolution
Let ![]() be a smooth function over the interval
be a smooth function over the interval ![]()
- If
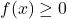 ,
, ![Rendered by QuickLaTeX.com x\in[a,b]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-f85b8fdd2b5a3f1cfcc82f4d20b3a4e5_l3.png) , then the area of the surface obtained by revolving the graph of
, then the area of the surface obtained by revolving the graph of 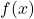 around the x-axis is given by
around the x-axis is given by
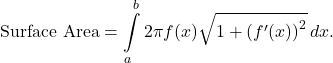
- If
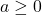 , then the area of the surface obtained by revolving the graph of
, then the area of the surface obtained by revolving the graph of 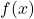 around the y-axis is given by
around the y-axis is given by
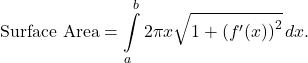
Similarly, let ![]() be a smooth function over the interval
be a smooth function over the interval ![]()
- If
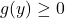 ,
, ![Rendered by QuickLaTeX.com y\in[c,d]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-ad9bfa20a8bf70033df3e88352068e05_l3.png) , then the area of the surface obtained by revolving the curve
, then the area of the surface obtained by revolving the curve 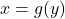 around the y-axis is given by
around the y-axis is given by
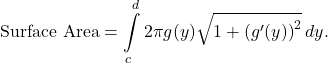
- If
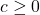 , then the area of the surface obtained by revolving the curve
, then the area of the surface obtained by revolving the curve 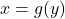 around the x-axis is given by
around the x-axis is given by
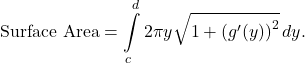
Calculating the Surface Area of a Surface of Revolution 1
Let ![]() over the interval
over the interval ![]() Find the surface area of the surface generated by revolving the graph of
Find the surface area of the surface generated by revolving the graph of ![]() around the x-axis.
around the x-axis.
Solution
The graph of ![]() and the surface of rotation are shown in the following figure.
and the surface of rotation are shown in the following figure.

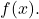 (b) The surface of revolution.
(b) The surface of revolution.We have ![]() Then,
Then, ![]() and
and ![]() Then,
Then,
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill \text{Surface Area}&\ds =\int\limits_{a}^{b}2\pi f(x)\sqrt{1+{({f}^{\prime }(x))}^{2}}\,dx \hfill \\[5mm]\ds &\ds =\int\limits_{1}^{4}2\pi \sqrt{x}\sqrt{1+\frac{1}{4x}}\,dx \hfill \\[5mm]\ds &\ds =\int\limits_{1}^{4}2\pi \sqrt{x+\frac{1}{4}}\,dx .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-3f82dfa6870151694300db11b19e64a0_l3.png)
Let ![]() Then,
Then, ![]() When
When ![]()
![]() and when
and when ![]()
![]() This gives us
This gives us
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill \int\limits_{0}^{1}2\pi \sqrt{x+\frac{1}{4}}\,dx &\ds =\int\limits_{5\text{/}4}^{17\text{/}4}2\pi \sqrt{u}du\hfill \\[5mm]\ds &\ds =2\pi {\left[\frac{2}{3}{u}^{3\text{/}2}\right]}\Big|_{5\text{/}4}^{17\text{/}4}=\frac{\pi }{6}\left[17\sqrt{17}-5\sqrt{5}\right].\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-d8e5feeca4ec2664a7bca7fd8d60d912_l3.png)
Let ![]() over the interval
over the interval ![]() Find the surface area of the surface generated by revolving the graph of
Find the surface area of the surface generated by revolving the graph of ![]() around the x-axis.
around the x-axis.
Answer
![]()
Hint
Use the process from the previous example.
Calculating the Surface Area of a Surface of Revolution 2
Let ![]() Consider the portion of the curve where
Consider the portion of the curve where ![]() Find the surface area of the surface generated by revolving the graph of
Find the surface area of the surface generated by revolving the graph of ![]() around the y-axis.
around the y-axis.
Solution
Notice that we are revolving the curve around the y-axis, and the interval is in terms of ![]() so we want to rewrite the function as a function of
so we want to rewrite the function as a function of ![]() . We get
. We get ![]() The graph of
The graph of ![]() and the surface of rotation are shown in the following figure.
and the surface of rotation are shown in the following figure.

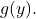 (b) The surface of revolution.
(b) The surface of revolution.We have ![]() so
so ![]() and
and ![]() Then
Then
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill \text{Surface Area}&\ds =\int\limits_{c}^{d}2\pi g(y)\sqrt{1+{({g}^{\prime }(y))}^{2}}\,dy\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{2}2\pi \left(\frac{1}{3}{y}^{3}\right)\sqrt{1+{y}^{4}}\,dy\hfill \\[5mm]\ds &\ds =\frac{2\pi }{3}\int\limits_{0}^{2}{y}^{3}\sqrt{1+{y}^{4}}\,dy.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7761acc78921228e27435d2e953534da_l3.png)
Let ![]() Then
Then ![]() When
When ![]()
![]() and when
and when ![]()
![]() Then
Then
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill \frac{2\pi }{3}\int\limits_{0}^{2}{y}^{3}\sqrt{1+{y}^{4}}\,dy&\ds =\frac{2\pi }{3}\int\limits_{1}^{17}\frac{1}{4}\sqrt{u}\,du\hfill \\[5mm]\ds &\ds =\frac{\pi }{6}{\left[\frac{2}{3}{u}^{3\text{/}2}\right]}\Big|_{1}^{17}=\frac{\pi }{9}\left[{(17)}^{3\text{/}2}-1\right].\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-dda6e7ba0ce945decf43a5b394500782_l3.png)
Let ![]() over the interval
over the interval ![]() Find the surface area of the surface generated by revolving the graph of
Find the surface area of the surface generated by revolving the graph of ![]() around the y-axis.
around the y-axis.
Answer
![]()
Hint
Use the process from the previous example.
Key Concepts
- The arc length of a curve can be calculated using a definite integral.
- The arc length is first approximated using line segments, which generates a Riemann sum. Taking a limit then gives us the definite integral formula. The same process can be applied to functions of
- The concepts used to calculate the arc length can be generalized to find the surface area of a surface of revolution.
- The integrals generated by both the arc length and surface area formulas are often difficult to evaluate.
Key Equations
- Arc Length of a Function of x
![Rendered by QuickLaTeX.com \ds \text{Arc Length}=\int\limits_{a}^{b}\sqrt{1+{\left[{f}^{\prime }(x)\right]}^{2}}\,dx](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-0c72fc5a01dbb6ddb78dffa38c486000_l3.png)
- Arc Length of a Function of y
![Rendered by QuickLaTeX.com \ds \text{Arc Length}=\int\limits_{c}^{d}\sqrt{1+{\left[{g}^{\prime }(y)\right]}^{2}}dy](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-5ed14a333416a02e4d5b9f6b2ef3f018_l3.png)
- Surface Area of a Function of x revolved about the x-axis
![Rendered by QuickLaTeX.com \ds \text{Surface Area}=\int\limits_{a}^{b}2\pi f(x)\sqrt{1+{[{f}^{\prime }(x)]}^{2}}\,dx](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-62e3e26a8e6d09f06ac0a28854fda875_l3.png)
- Surface Area of a Function of x revolved about the y-axis
![Rendered by QuickLaTeX.com \ds \text{Surface Area}=\int\limits_{a}^{b}2\pi x\sqrt{1+{[{f}^{\prime }(x)]}^{2}}\,dx](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-9a252ffa234dba200689f9b5d8308350_l3.png)
- Surface Area of a Function of y revolved about the y-axis
![Rendered by QuickLaTeX.com \ds \text{Surface Area}=\int\limits_{c}^{d}2\pi g(y)\sqrt{1+{[{g}^{\prime }(y)]}^{2}}\,dy](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-bf1fc857dac4f57b01bac920afb37111_l3.png)
- Surface Area of a Function of y revolved about the x-axis
![Rendered by QuickLaTeX.com \ds \text{Surface Area}=\int\limits_{c}^{d}2\pi y\sqrt{1+{[{g}^{\prime }(y)]}^{2}}\,dy](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-9d8097f3eab9cb74a040a6800ac35e7c_l3.png)
Exercises
For the following exercises, find the length of the curve with the given equation over the specified interval.
1. ![]()
Answer
![]()
2. ![]()
3. ![]()
Answer
![]()
4. Pick an arbitrary linear function ![]() over any interval of your choice
over any interval of your choice ![]() Determine the length of the corresponding curve with calculus and then verify the answer is correct by using geometry.
Determine the length of the corresponding curve with calculus and then verify the answer is correct by using geometry.
5. Find the surface area of the surface generated when the curve ![]() from
from ![]() to
to ![]() revolves around the x-axis, as shown below.
revolves around the x-axis, as shown below.

Answer
![]()
6. Find the surface area of the surface generated when the curve ![]() from
from ![]() to
to ![]() revolves around the y-axis.
revolves around the y-axis.

For the following exercises, find the lengths of the given curves. If you cannot evaluate the integral, leave your answer in the integral form (set up).
7. ![]() from
from ![]()
Answer
![]()
8. ![]() from
from ![]()
(Hint: rewrite the equation of the curve in the form ![]() .)
.)
9. ![]() from
from ![]()
Answer
![]()
10. ![]() from
from ![]() to
to ![]()
11. [Set Up] ![]() on
on ![]() to
to ![]()
Answer
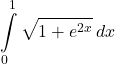
12. ![]() from
from ![]()
13. ![]() from
from ![]()
Answer
![]()
14. ![]() from
from ![]()
15. ![]() from
from ![]()
Answer
10
16. [Set Up] ![]() from
from ![]()
17. ![]() from
from ![]() to
to ![]()
Answer
![]()
18. ![]() from
from ![]()
19. ![]() from
from ![]() to
to ![]()
Answer
![]()
20. [Set Up] ![]() from
from ![]() to
to ![]()
21. [Set Up] ![]() from
from ![]()
Answer
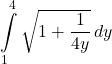
22. ![]() from
from ![]() to
to ![]()
23. [Set Up] ![]() from
from ![]() to
to ![]()
Answer
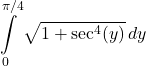
24. [Set Up] ![]() from
from ![]() to
to ![]()
25. [Set Up] ![]() from
from ![]()
Answer
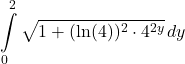
26. [Set Up] ![]() from
from ![]() to
to ![]()
For the following exercises, find the surface area of the surface generated when the given curve revolves around the x-axis. If you cannot evaluate the integral, leave your answer in the integral form (set up).
27. ![]() from
from ![]() to
to ![]()
Answer
![]()
28. ![]() from
from ![]() to
to ![]()
29. ![]() from
from ![]()
Answer
![]()
30. [Set Up] ![]() from
from ![]()
31. ![]() from
from ![]()
Answer
![]()
32. ![]() from
from ![]()
33. ![]() from
from ![]()
Answer
![]()
34. [Set Up] ![]() from
from ![]()
For the following exercises, find the surface area of the surface generated when the given curve revolves around the y-axis. If you cannot evaluate the integral, leave your answer in the integral (set up) form.
35. ![]() from
from ![]()
Answer
![]()
36. ![]() from
from ![]()
37. ![]() from
from ![]()
Answer
![]()
38. [Set Up] ![]() from
from ![]() to
to ![]()
39. ![]() from
from ![]()
Answer
![]()
40. [Set Up] ![]() from
from ![]() to
to ![]()
41. [Set Up] ![]() from
from ![]() to
to ![]()
Answer
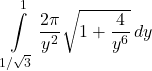
42. [Set Up] ![]() from
from ![]() to
to ![]()
43. The base of a lamp is constructed by revolving a quarter circle ![]() around the y-axis from
around the y-axis from ![]() to
to ![]() as shown below. Set up an integral for the surface area of the base of the lamp and compute it.
as shown below. Set up an integral for the surface area of the base of the lamp and compute it.

Answer
![]()
44. A light bulb is a sphere with radius ![]() in. with the bottom sliced off to fit onto a cylinder of radius
in. with the bottom sliced off to fit onto a cylinder of radius ![]() in. and hight
in. and hight ![]() in., as shown below. The sphere is cut off at the bottom to fit exactly onto the cylinder, so the radius of the cut is
in., as shown below. The sphere is cut off at the bottom to fit exactly onto the cylinder, so the radius of the cut is ![]() in. Find the surface area of the light bulb (not including the top or bottom of the cylinder).
in. Find the surface area of the light bulb (not including the top or bottom of the cylinder).

45. [Set Up] A lampshade is constructed by rotating a curve ![]() around the y-axis from
around the y-axis from ![]() to
to ![]() as shown below. Set up an integral for the amount of material you would need to construct this lampshade, that is, its surface area.
as shown below. Set up an integral for the amount of material you would need to construct this lampshade, that is, its surface area.

Answer
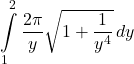
46. [Set Up] An anchor drags behind a boat according to the function ![]() where
where ![]() represents the depth beneath the boat and
represents the depth beneath the boat and ![]() is the horizontal distance to the anchor from the back of the boat. If the anchor is 23 ft below the boat, set up the integral to determine how much rope you have to pull to reach the anchor.
is the horizontal distance to the anchor from the back of the boat. If the anchor is 23 ft below the boat, set up the integral to determine how much rope you have to pull to reach the anchor.
47. [Set Up] You are building a bridge that will span 10 ft. You intend to add decorative rope in the shape of ![]() where
where ![]() is the distance in feet from one end of the bridge. Set up the integral to determine how much rope you need.
is the distance in feet from one end of the bridge. Set up the integral to determine how much rope you need.
Answer
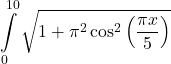
48. Find the arc length of the curve ![]() from
from ![]() to
to ![]()
(Hint: Recall trigonometric identities.)
Glossary
- arc length
- the arc length of a curve can be thought of as the distance a person would travel along the path of the curve
- frustum
- a portion of a cone; a frustum is constructed by cutting the cone with a plane parallel to the base
- surface area
- the surface area of a solid is the total area of the outer layer of the object; for objects such as cubes or bricks, the surface area of the object is the sum of the areas of all of its faces


Hint
Use the process from the previous example. Don’t forget to change the limits of integration.