0.2 Derivatives of Inverse Trigonometric Functions
Learning Objectives
- Calculate the derivative of an inverse function.
- Recognize the derivatives of the standard inverse trigonometric functions.
In this section, we explore the relationship between the derivative of a function and the derivative of its inverse. We will use this relationship to find derivatives of inverse trigonometric functions.
The Derivative of an Inverse Function
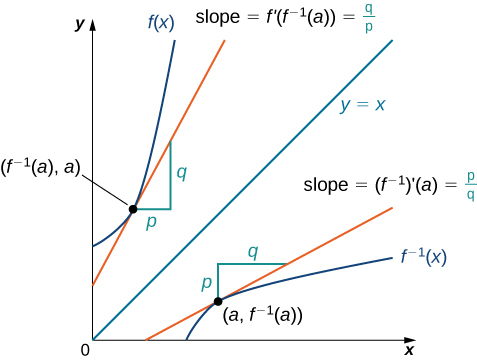
We begin by considering a function and its inverse. If ![]() is both invertible and differentiable, it seems reasonable that the inverse of
is both invertible and differentiable, it seems reasonable that the inverse of ![]() is also differentiable. Let us look at the graphs of a function
is also differentiable. Let us look at the graphs of a function ![]() and its inverse
and its inverse ![]() on Figure 1 below. Consider the point
on Figure 1 below. Consider the point ![]() on the graph of
on the graph of ![]() having a tangent line with a slope of
having a tangent line with a slope of ![]() . As we discussed in the previous section, the graphs of
. As we discussed in the previous section, the graphs of ![]() and
and ![]() are symmetric with respect to the line
are symmetric with respect to the line ![]() . Therefore, the tangent line to the curve
. Therefore, the tangent line to the curve ![]() at the point
at the point ![]() must be symmetric to the tangent line to the curve
must be symmetric to the tangent line to the curve ![]() at the (symmetric) point
at the (symmetric) point ![]() . Note that the product of slopes of the lines that are symmetric with respect to the line
. Note that the product of slopes of the lines that are symmetric with respect to the line ![]() is 1. Indeed, if a line has equation
is 1. Indeed, if a line has equation ![]() , symmetric one would have equation
, symmetric one would have equation ![]() (switching
(switching ![]() and
and ![]() ), which is equivalent to
), which is equivalent to ![]() , provided
, provided ![]() . Thus, if
. Thus, if ![]() is differentiable at
is differentiable at ![]() , then it must be the case that
, then it must be the case that
We may also derive the formula for the derivative of the inverse by first recalling that ![]() for every
for every ![]() in the domain of
in the domain of ![]() . Then by differentiating both sides of this equation (using the chain rule on the right), we obtain
. Then by differentiating both sides of this equation (using the chain rule on the right), we obtain
![]() .
.
Solving for ![]() , we obtain
, we obtain
![]() .
.
We summarize the above in the following theorem.
Inverse Function Theorem
Let ![]() be a function that is both invertible and differentiable. Let
be a function that is both invertible and differentiable. Let ![]() be the inverse of
be the inverse of ![]() . For all
. For all ![]() satisfying
satisfying ![]() ,
,
![]() .
.
In other words, if we let ![]() be the inverse of
be the inverse of ![]() , then
, then
![]() whenever
whenever ![]() .
.
Derivatives of Inverse Trigonometric Functions
We now use the inverse function theorem to find derivatives of inverse trigonometric functions. These derivatives will prove invaluable in the study of integration later in this text.
Derivative of the Inverse Sine Function
Use the inverse function theorem to find the derivative of ![]() .
.
Solution
Since ![]() is differentiable and invertible when restricted to the interval
is differentiable and invertible when restricted to the interval ![]() , as per the above theorem, for
, as per the above theorem, for ![]() , we have that
, we have that ![]() whenever
whenever ![]() . Because
. Because ![]() , we need to compute
, we need to compute ![]() .
.
Let ![]() . Then
. Then ![]() , and we want to find
, and we want to find ![]() . Since
. Since ![]() on
on ![]() , it follows from the Pythagorean trigonometric identity
, it follows from the Pythagorean trigonometric identity ![]() that
that ![]() .
.
The domain of ![]() is
is ![]() and
and ![]() for every
for every ![]() . Therefore,
. Therefore,
Use the inverse function theorem to find the derivative of ![]() .
.
Answer
![]()
The derivatives of the remaining inverse trigonometric functions may also be found by using the inverse function theorem. The corresponding formulas are provided in the following theorem.
Derivatives of Inverse Trigonometric Functions
![Rendered by QuickLaTeX.com \begin{array}{lllll}\ds\frac{d}{dx}\big(\ds\sin^{-1} (x)\big)=\large \frac{1}{\sqrt{1-x^2}}& \big(x\in(-1,1)\big) & & \ds\frac{d}{dx}\big(\cos^{-1} (x)\big)=\large \frac{-1}{\sqrt{1-x^2}}& \big(x\in(-1,1)\big)\\[4mm] \ds\frac{d}{dx}\big(\tan^{-1} (x)\big)=\large \frac{1}{1+x^2} & \big(x\in\mathbb{R}\big) & & \ds\frac{d}{dx}\big(\cot^{-1} (x)\big)=\large \frac{-1}{1+x^2} & \big(x\in\mathbb{R}\big) \\[4mm] \ds\frac{d}{dx}\big(\sec^{-1} (x)\big)=\large \frac{1}{|x|\sqrt{x^2-1}} & \big(|x|>1\big) & & \ds\frac{d}{dx}\big(\csc^{-1} (x)\big)=\large \frac{-1}{|x|\sqrt{x^2-1}} & \big(|x|>1\big) \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-5e160c90cb5324a2b7dc9d131f6f0494_l3.png)
Applying Formulas for the Derivatives of Inverse Trigonometric Functions
Find the derivatives of the following functions.
Solution
- We apply the chain rule with outside function
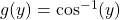 and inside function
and inside function ![Rendered by QuickLaTeX.com \ds h(x)=x\sqrt[3]x=x^{1+\frac13}=x^{\frac43}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-493966d8e54f56d6f89c48b7b6c59090_l3.png) to obtain
to obtain ![Rendered by QuickLaTeX.com \ds \Big(\cos^{-1}\big(x\sqrt[3]x\big)\Big)'=\big(g(h(x))\big)'=g'(h(x))\cdot h'(x)](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-00548bd64b08ca9d52eba18359135790_l3.png)
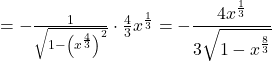
- Here we need to apply the product rule to the multiples
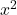 and
and 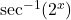 , while differentiating
, while differentiating 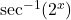 requires using the chain rule. We have
requires using the chain rule. We have 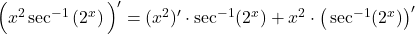
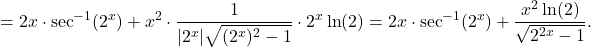
Key Concepts
- The inverse function theorem allows us to compute derivatives of inverse functions without using the limit definition of the derivative.
- We can use the inverse function theorem to develop differentiation formulas for the inverse trigonometric functions.
Key Equations
- Inverse function theorem
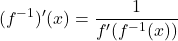 whenever
whenever 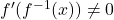 and
and 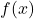 is differentiable.
is differentiable. - Derivative of inverse sine function
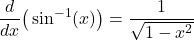
- Derivative of inverse cosine function
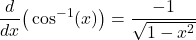
- Derivative of inverse tangent function
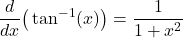
- Derivative of inverse cotangent function
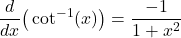
- Derivative of inverse secant function
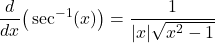
- Derivative of inverse cosecant function
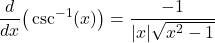 .
.
Exercises
For the following exercises, find ![]() .
.
1. ![]()
Answer
![]()
2. ![]()
3. ![]()
Answer
![]()
4. ![]()
5. ![]()
Answer
![]()
6. ![]()
7. ![]()
Answer
![]()
8. ![]()
9. ![]()
Answer
![]()
10. ![]()
For the following exercises, find the slope of the tangent line to the given curve at the given point.
11. ![]() at
at ![]() .
.
Answer
![]()
13*. ![]() at
at ![]() .
.
(Hint: Use implicit differentiation.)
Answer
![]()
14*. There is a theorem that if a function ![]() is differentiable on an open interval
is differentiable on an open interval ![]() and
and ![]() on
on ![]() then
then ![]() is constant on
is constant on ![]() . Using this result, prove that
. Using this result, prove that ![]() ,
, ![]() .
.
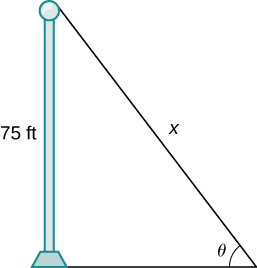
15. [T] A pole stands 75 feet tall. An angle ![]() is formed when wires of various lengths
is formed when wires of various lengths ![]() (measured in feet) are attached from the ground to the top of the pole, as shown in the following figure. Find the rate of change
(measured in feet) are attached from the ground to the top of the pole, as shown in the following figure. Find the rate of change ![]() of the angle with respect to the wire length when a wire of length 90 feet is attached.
of the angle with respect to the wire length when a wire of length 90 feet is attached.
Answer
![]() radians per foot
radians per foot
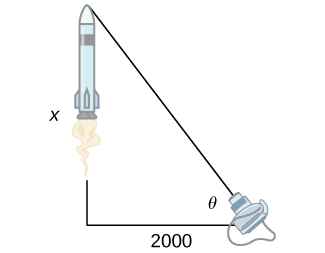
16. [T] A television camera at ground level is 2000 feet away from the launching pad of a space rocket that is set to take off vertically, as seen in the following figure. After launch, let ![]() be the height of the rocket and
be the height of the rocket and ![]() be the angle of elevation of the camera. Find the rate of change
be the angle of elevation of the camera. Find the rate of change ![]() of the angle of elevation with respect to the rocket’s height when the camera and the rocket are 5000 feet apart.
of the angle of elevation with respect to the rocket’s height when the camera and the rocket are 5000 feet apart.
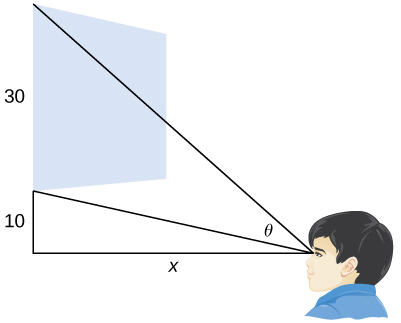
17*. A local movie theatre has a 30-foot-high screen that is 10 feet above a person’s eye level when seated. Suppose that a person is sitting at a distance of ![]() feet from the movie screen and has a viewing angle of
feet from the movie screen and has a viewing angle of ![]() radians, see the figure below.
radians, see the figure below.
- Find
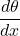 .
. - Use optimization methods learned in Calculus 1 to determine at what distance
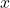 the person should sit to maximize his or her viewing angle.
the person should sit to maximize his or her viewing angle.
Answer
a. ![]()
b. The optimal distance ![]() for maximizing the viewing angle is 20 feet.
for maximizing the viewing angle is 20 feet.

