2.2 Determining Volumes by Slicing
Learning Objectives
- Determine the volume of a solid by integrating an area of a cross-section (the slicing method).
- Find the volume of a solid of revolution using the disk method.
- Find the volume of a solid of revolution with a cavity using the washer method.
In the preceding section, we used definite integrals to find the area between two curves. In this section, we use definite integrals to find volumes of three-dimensional solids. We consider three approaches—slicing, disks, and washers—for finding these volumes, depending on the characteristics of the solid.
Volume and the Slicing Method
Just as area is the numerical measure of a two-dimensional region, volume is the numerical measure of a three-dimensional solid. Most of us have computed volumes of solids by using basic geometric formulas. The volume of a rectangular solid, for example, can be computed by multiplying length, width, and height: ![]() The formulas for the volume of a sphere
The formulas for the volume of a sphere ![]() a cone
a cone ![]() and a pyramid
and a pyramid ![]() have also been introduced. Although some of these formulas were derived using geometry alone, all of them can be obtained by using integration.
have also been introduced. Although some of these formulas were derived using geometry alone, all of them can be obtained by using integration.
We can also calculate the volume of a cylinder. Although most of us think of a cylinder as having a circular base, such as a soup can or a metal rod, in mathematics the word cylinder has a more general meaning. To discuss cylinders in this more general context, we first need to define some vocabulary.
We define the cross-section of a solid to be the intersection of a plane with the solid. A cylinder is defined as any solid that can be generated by translating a plane region along a line perpendicular to the region, called the axis of the cylinder. Thus, all cross-sections perpendicular to the axis of a cylinder are identical. The solid shown in below is an example of a cylinder with a noncircular base. To calculate the volume of a cylinder, we simply multiply the area of the cross-section by the height of the cylinder: ![]() In the case of a right circular cylinder (soup can), this becomes
In the case of a right circular cylinder (soup can), this becomes ![]()

If a solid does not have a constant cross-section (and it is not one of the other basic solids), we may not have a formula for its volume. In this case, we can use a definite integral to calculate the volume of the solid. We do this by slicing the solid into pieces, estimating the volume of each slice, and then adding those estimated volumes together. The slices should all be parallel to one another, and when we put all the slices together, we should get the whole solid. Consider, for example, the solid S shown in below , extending along the x-axis.

We want to divide ![]() into slices perpendicular to the x-axis. As we see later in the chapter, there may be times when we want to slice the solid in some other direction—say, with slices perpendicular to the y-axis. The decision of which way to slice the solid is very important. If we make the wrong choice, the computations can get quite messy. Later in the chapter, we examine some of these situations in detail and look at how to decide which way to slice the solid. For the purposes of this section, however, we use slices perpendicular to the x-axis.
into slices perpendicular to the x-axis. As we see later in the chapter, there may be times when we want to slice the solid in some other direction—say, with slices perpendicular to the y-axis. The decision of which way to slice the solid is very important. If we make the wrong choice, the computations can get quite messy. Later in the chapter, we examine some of these situations in detail and look at how to decide which way to slice the solid. For the purposes of this section, however, we use slices perpendicular to the x-axis.
Because the cross-sectional area is not constant, we let ![]() represent the area of the cross-section at point
represent the area of the cross-section at point ![]() Now let
Now let ![]() be a regular partition of
be a regular partition of ![]() and for
and for ![]() let
let ![]() represent the slice of the solid
represent the slice of the solid ![]() stretching from
stretching from ![]() The following figure shows the sliced solid with
The following figure shows the sliced solid with ![]()

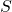 has been divided into three slices perpendicular to the x-axis.
has been divided into three slices perpendicular to the x-axis.Finally, for ![]() let
let ![]() be an arbitrary point in
be an arbitrary point in ![]() Then the volume of slice
Then the volume of slice ![]() can be estimated by
can be estimated by ![]() Adding these approximations together, we see that the volume of the entire solid
Adding these approximations together, we see that the volume of the entire solid ![]() can be approximated by
can be approximated by
By now, we can recognize this as a Riemann sum, and our next step is to take the limit as ![]() Then we have
Then we have
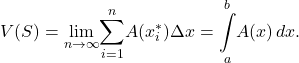
The technique we have just described is called the slicing method . To apply it, we use the following strategy.
Problem-Solving Strategy: Finding Volumes by the Slicing Method
- Examine the solid and determine the shape of a cross-section of the solid. It is often helpful to draw a picture if one is not provided.
- Determine a formula for the area of the cross-section.
- Integrate the area expression over the appropriate interval to get the volume.
Recall that in this section, we assume the slices are perpendicular to the x-axis. Therefore, the area expression is in terms of x and the limits of integration lie on the x-axis. However, the problem-solving strategy shown here is valid regardless of how we choose to slice the solid.
Deriving the Formula for the Volume of a Pyramid
We know from geometry that the formula for the volume of a pyramid is ![]() If the pyramid has a square base, this becomes
If the pyramid has a square base, this becomes ![]() where
where ![]() denotes the length of one side of the base. We are going to use the slicing method to derive this formula.
denotes the length of one side of the base. We are going to use the slicing method to derive this formula.
Solution
We want to apply the slicing method to a pyramid with a square base. To set up the integral, consider the pyramid shown in below, oriented along the x-axis.

We first want to determine the shape of a cross-section of the pyramid. Since the base is a square, the cross-sections are squares as well (step 1). Now we want to determine a formula for the area of one of these cross-sectional squares. Looking at Figure 4 (b), and using a proportion, since these are similar triangles, we have
Therefore, the area of one of the cross-sectional squares is
Then we find the volume of the pyramid by integrating from ![]() (step
(step ![]()
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill V&\ds =\underset{0}{\overset{h}{\int }}A(x)\,dx \hfill \\[5mm]\ds &\ds =\underset{0}{\overset{h}{\int }}{\left(\frac{ax}{h}\right)}^{2}\,dx =\frac{{a}^{2}}{{h}^{2}}\underset{0}{\overset{h}{\int }}{x}^{2}\,dx \hfill \\[5mm]\ds &\ds ={\left[\frac{{a}^{2}}{{h}^{2}}\left(\frac{1}{3}{x}^{3}\right)\right]}\Big|_{0}^{h}=\frac{1}{3}{a}^{2}h.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-b58565553e3f15b11e3053bd8fa70a84_l3.png)
This is the formula we were looking for.
Use the slicing method to derive the formula ![]() for the volume of a circular cone.
for the volume of a circular cone.
Solids of Revolution
If a region in a plane is revolved around a line in that plane, the resulting solid is called a solid of revolution , as shown in the following figure.
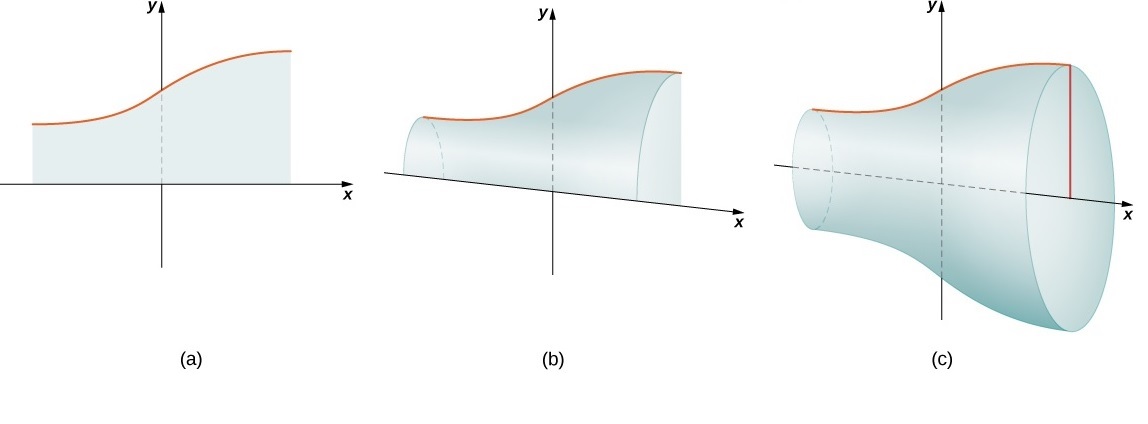
Solids of revolution are common in mechanical applications, such as machine parts produced by a lathe. We spend the rest of this section looking at solids of this type. The next example uses the slicing method to calculate the volume of a solid of revolution.
Use an online integral calculator by WolframAlpha to learn more.
Using the Slicing Method to find the Volume of a Solid of Revolution
Use the slicing method to find the volume of the solid of revolution bounded by the graphs of ![]() and
and ![]() and rotated about the x-axis.
and rotated about the x-axis.
Solution
Using the problem-solving strategy, we first sketch the graph of the quadratic function over the interval ![]() as shown in the following figure.
as shown in the following figure.

Next, revolve the region around the x-axis, as shown in the following figure.

Since the solid was formed by revolving the region around the x-axis, the cross-sections are circles (step 1). The area of the cross-section, then, is the area of a circle, and the radius of the circle is given by ![]() Use the formula for the area of the circle:
Use the formula for the area of the circle:
The volume, then, is (step 3)
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill V&\ds =\underset{a}{\overset{h}{\int }}A(x)\,dx \hfill \\[5mm]\ds &\ds =\int\limits_{1}^{4}\pi {({x}^{2}-4x+5)}^{2}\,dx =\pi \int\limits_{1}^{4}({x}^{4}-8{x}^{3}+26{x}^{2}-40x+25)\,dx \hfill \\[5mm]\ds &\ds ={\pi \left(\frac{{x}^{5}}{5}-2{x}^{4}+\frac{26{x}^{3}}{3}-20{x}^{2}+25x\right)}\Big|_{1}^{4}=\frac{78}{5}\pi .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-b83271fadc14582661f8e434e69527f7_l3.png)
The volume is ![]()
Use the method of slicing to find the volume of the solid of revolution formed by revolving the region between the graph of the function ![]() and the x-axis over the interval
and the x-axis over the interval ![]() around the x-axis. See the following figure.
around the x-axis. See the following figure.

Answer
![]()
The Disk Method
When we use the slicing method with solids of revolution, it is often called the disk method because, for solids of revolution, the slices used to over approximate the volume of the solid are disks. To see this, consider the solid of revolution generated by revolving the region between the graph of the function ![]() and the x-axis over the interval
and the x-axis over the interval ![]() around the x-axis. The graph of the function and a representative disk are shown in Figure 8 (a) and (b). The region of revolution and the resulting solid are shown in Figure 8 (c) and (d).
around the x-axis. The graph of the function and a representative disk are shown in Figure 8 (a) and (b). The region of revolution and the resulting solid are shown in Figure 8 (c) and (d).
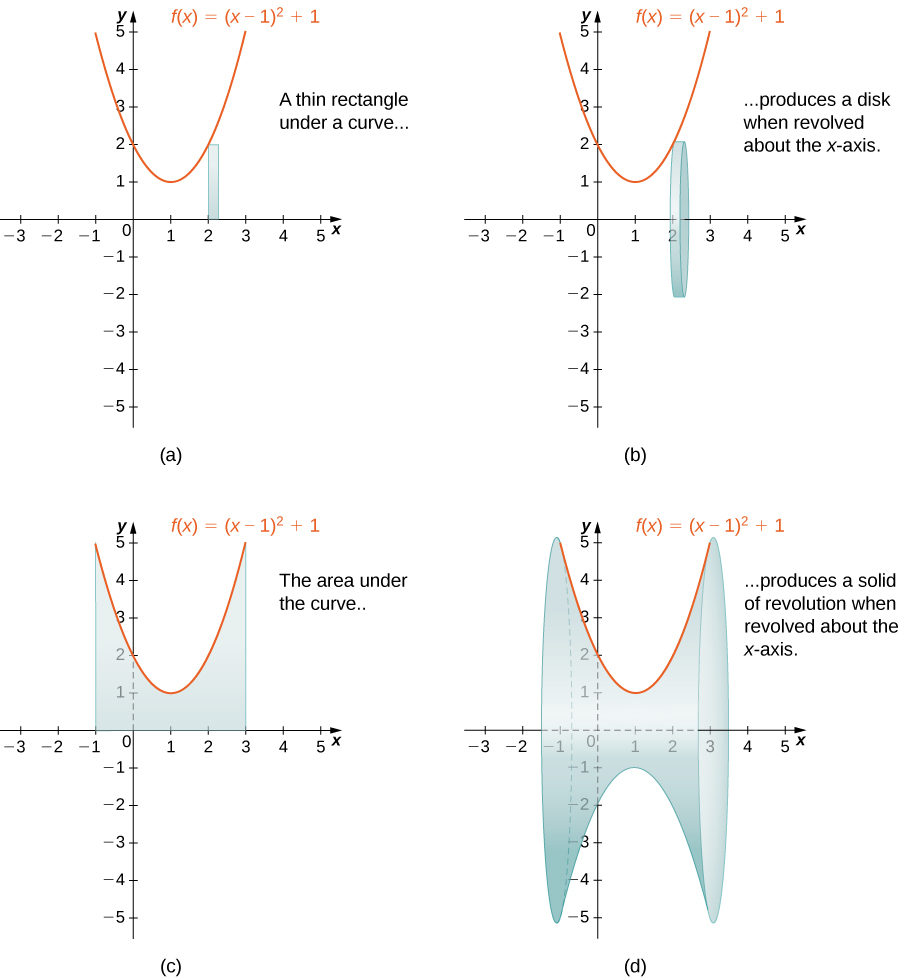
We already used the formal Riemann sum development of the volume formula when we developed the slicing method. We know that
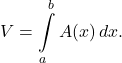
The only difference with the disk method is that we know the formula for the cross-sectional area ahead of time; it is the area of a circle. This gives the following method.
The Disk Method
Let ![]() be continuous and nonnegative. Define
be continuous and nonnegative. Define ![]() as the region bounded above by the graph of
as the region bounded above by the graph of ![]() below by the x-axis, on the left by the line
below by the x-axis, on the left by the line ![]() and on the right by the line
and on the right by the line ![]() Then, the volume of the solid of revolution formed by revolving
Then, the volume of the solid of revolution formed by revolving ![]() around the x-axis is given by
around the x-axis is given by
![Rendered by QuickLaTeX.com \ds V=\int\limits_{a}^{b}\pi {\left[f(x)\right]}^{2}\,dx .](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-d1ea9eaf6bc098c2744abdf24809f0e4_l3.png)
The volume of the solid we have been studying is given by
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill V&\ds =\int\limits_{a}^{b}\pi {\left[f(x)\right]}^{2}\,dx \hfill \\[5mm]\ds &\ds =\int\limits_{-1}^{3}\pi {\left[{(x-1)}^{2}+1\right]}^{2}\,dx =\pi \int\limits_{-1}^{3}{\left[{(x-1)}^{4}+2{(x-1)}^{2}+1\right]}^{2}\,dx \hfill \\[5mm]\ds &\ds =\pi {\left[\frac{1}{5}{(x-1)}^{5}+\frac{2}{3}{(x-1)}^{3}+x\right]}\Big|_{-1}^{3}=\pi \left[\left(\frac{32}{5}+\frac{16}{3}+3\right)-\left(-\frac{32}{5}-\frac{16}{3}-1\right)\right]=\frac{412\pi }{15}\ {\text{units}}^{3}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-3f10949b63675439688b71730922a792_l3.png)
Let’s look at some examples.
Using the Disk Method to Find the Volume of a Solid of Revolution 1
Use the disk method to find the volume of the solid of revolution generated by rotating the region between the graph of ![]() and the x-axis over the interval
and the x-axis over the interval ![]() around the x-axis.
around the x-axis.
Solution
The graphs of the function and the solid of revolution are shown in the following figure.

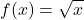 over the interval
over the interval ![Rendered by QuickLaTeX.com \ds \left[1,4\right].](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-b376e0069be1b2c974cc268186756636_l3.png) (b) The solid of revolution obtained by revolving the region under the graph of
(b) The solid of revolution obtained by revolving the region under the graph of 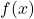 about the x-axis.
about the x-axis.We have
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill V&\ds =\int\limits_{a}^{b}\pi {\left[f(x)\right]}^{2}\,dx \hfill \\[5mm]\ds &\ds =\int\limits_{1}^{4}\pi {\left[\sqrt{x}\right]}^{2}\,dx =\pi \int\limits_{1}^{4}x\,dx \hfill \\[5mm]\ds &\ds ={\frac{\pi }{2}{x}^{2}}\Big|_{1}^{4}=\frac{15\pi }{2}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-d5fc82569f4497c759250bdafbfd41b0_l3.png)
The volume is ![]() units 3 .
units 3 .
Use the disk method to find the volume of the solid of revolution generated by rotating the region between the graph of ![]() and the x-axis over the interval
and the x-axis over the interval ![]() around the x-axis.
around the x-axis.
Answer
![]() units 3
units 3
So far, our examples have all concerned regions revolved around the x-axis, but we can generate a solid of revolution by revolving a plane region around any horizontal or vertical line. In the next example, we look at a solid of revolution that has been generated by revolving a region around the y-axis. The mechanics of the disk method are nearly the same as when the x-axis is the axis of revolution, but we express the function in terms of y and we integrate with respect to y as well. This is summarized in the following rule.
The Disk Method for Solids of Revolution around the y-axis
Let ![]() be continuous and nonnegative. Define
be continuous and nonnegative. Define ![]() as the region bounded on the right by the graph of
as the region bounded on the right by the graph of ![]() on the left by the y-axis, below by the line
on the left by the y-axis, below by the line ![]() and above by the line
and above by the line ![]() Then, the volume of the solid of revolution formed by revolving
Then, the volume of the solid of revolution formed by revolving ![]() around the y-axis is given by
around the y-axis is given by
![Rendered by QuickLaTeX.com \ds V=\int\limits_{c}^{d}\pi {\left[g(y)\right]}^{2}dy.](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-0e01f75bc1df99f7ec08324d6a0d6dba_l3.png)
The next example shows how this rule works in practice.
Using the Disk Method to Find the Volume of a Solid of Revolution 2
Let ![]() be the region bounded by the graph of
be the region bounded by the graph of ![]() and the y-axis over the y-axis interval
and the y-axis over the y-axis interval ![]() Use the disk method to find the volume of the solid of revolution generated by rotating
Use the disk method to find the volume of the solid of revolution generated by rotating ![]() around the y-axis.
around the y-axis.
Solution
Figure 10 shows the function and a representative disk that can be used to estimate the volume. Notice that since we are revolving the function around the y-axis, the disks are horizontal, rather than vertical.

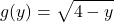 and the y-axis. (b) The rectangle forms a representative disk after revolution around the y-axis.
and the y-axis. (b) The rectangle forms a representative disk after revolution around the y-axis.The region to be revolved and the full solid of revolution are depicted in the following figure.
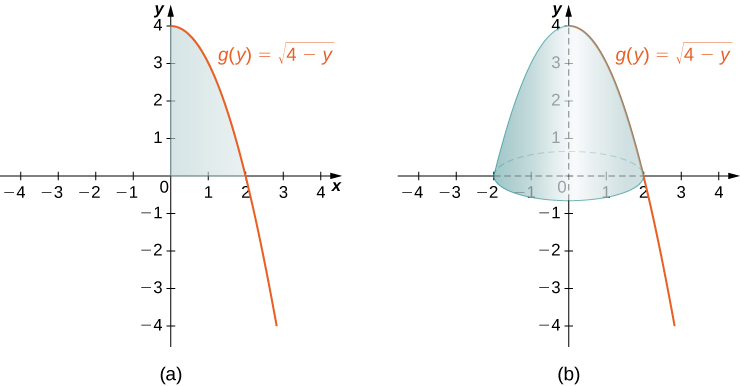
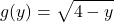 over the y-axis interval
over the y-axis interval ![Rendered by QuickLaTeX.com \ds \left[0,4\right].](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-47cf87a8ffe975c087ef1c3f08a74e57_l3.png) (b) The solid of revolution formed by revolving the region about the y-axis.
(b) The solid of revolution formed by revolving the region about the y-axis.To find the volume, we integrate with respect to ![]() We obtain
We obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill V&\ds =\int\limits_{c}^{d}\pi {\left[g(y)\right]}^{2}dy\hfill \\[5mm]\ds &\ds =\int\limits_{0}^{4}\pi {\left[\sqrt{4-y}\right]}^{2}dy=\pi \int\limits_{0}^{4}(4-y)dy\hfill \\[5mm]\ds &\ds ={\pi \left[4y-\frac{{y}^{2}}{2}\right]}\Big|_{0}^{4}=8\pi .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-ac4723775683190e595ee8a07284beba_l3.png)
The volume is ![]() units 3 .
units 3 .
Use the disk method to find the volume of the solid of revolution generated by rotating the region between the graph of ![]() and the y-axis over the interval
and the y-axis over the interval ![]() around the y-axis.
around the y-axis.
Answer
![]() units 3
units 3
The Washer Method
Some solids of revolution have cavities in the middle; they are not solid all the way to the axis of revolution. Sometimes, this is just a result of the way the region of revolution is shaped with respect to the axis of revolution. In other cases, cavities arise when the region of revolution is defined as the region between the graphs of two functions. A third way this can happen is when an axis of revolution other than the x-axis or y-axis is selected.
When the solid of revolution has a cavity in the middle, the slices used to approximate the volume are not disks, but washers (disks with holes in the center). For example, consider the region bounded above by the graph of the function ![]() and below by the graph of the function
and below by the graph of the function ![]() over the interval
over the interval ![]() When this region is revolved around the x-axis, the result is a solid with a cavity in the middle, and the slices are washers. The graph of the function and a representative washer are shown in Figure 12 (a) and (b). The region of revolution and the resulting solid are shown in Figure 12 (c) and (d).
When this region is revolved around the x-axis, the result is a solid with a cavity in the middle, and the slices are washers. The graph of the function and a representative washer are shown in Figure 12 (a) and (b). The region of revolution and the resulting solid are shown in Figure 12 (c) and (d).

The cross-sectional area, then, is the area of the outer circle less the area of the inner circle. In this case,
Then the volume of the solid is
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill V&\ds =\int\limits_{a}^{b}A(x)\,dx \hfill \\[5mm]\ds &\ds =\int\limits_{1}^{4}\pi (x-1)\,dx ={\pi \left[\frac{{x}^{2}}{2}-x\right]}\Big|_{1}^{4}=\frac{9}{2}\pi \ {\text{units}}^{3}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-e2dfd77a18de9133405afad87fdf9997_l3.png)
Generalizing this process gives the washer method .
The Washer Method
Suppose ![]() and
and ![]() are continuous, nonnegative functions such that
are continuous, nonnegative functions such that ![]() over
over ![]() Let
Let ![]() denote the region bounded above by the graph of
denote the region bounded above by the graph of ![]() below by the graph of
below by the graph of ![]() on the left by the line
on the left by the line ![]() and on the right by the line
and on the right by the line ![]() Then, the volume of the solid of revolution formed by revolving
Then, the volume of the solid of revolution formed by revolving ![]() around the x-axis is given by
around the x-axis is given by
![Rendered by QuickLaTeX.com \ds V=\int\limits_{a}^{b}\pi \left[{(f(x))}^{2}-{(g(x))}^{2}\right]\,dx .](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-a394acb7c00cf4591973299ae478d7dc_l3.png)
Using the Washer Method
Find the volume of a solid of revolution formed by revolving the region bounded above by the graph of ![]() and below by the graph of
and below by the graph of ![]() over the interval
over the interval ![]() around the x-axis.
around the x-axis.
Solution
The graphs of the functions and the solid of revolution are shown in the following figure.

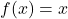 and
and 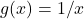 over the interval
over the interval ![Rendered by QuickLaTeX.com \ds \left[1,4\right].](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-b376e0069be1b2c974cc268186756636_l3.png) (b) Revolving the region about the x-axis generates a solid of revolution with a cavity in the middle.
(b) Revolving the region about the x-axis generates a solid of revolution with a cavity in the middle.We have
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill V&\ds =\int\limits_{a}^{b}\pi \left[{(f(x))}^{2}-{(g(x))}^{2}\right]\,dx \hfill \\[5mm]\ds &\ds =\pi \int\limits_{1}^{4}\left[{x}^{2}-{\left(\frac{1}{x}\right)}^{2}\right]\,dx \text{}={\pi \left[\frac{{x}^{3}}{3}+\frac{1}{x}\right]}\Big|_{1}^{4}=\frac{81\pi }{4}\ {\text{units}}^{3}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-935f566b4d21e59d9e50cdd4e6498f95_l3.png)
Find the volume of a solid of revolution formed by revolving the region bounded by the graphs of ![]() and
and ![]() over the interval
over the interval ![]() around the x-axis.
around the x-axis.
Answer
![]() units 3
units 3
Hint
Graph the functions to determine which graph forms the upper bound and which graph forms the lower bound, then use the procedure from the above example.
As with the disk method, we can also apply the washer method to solids of revolution that result from revolving a region around the y-axis. In this case, the following rule applies.
Rule: The Washer Method for Solids of Revolution around the y-axis
Suppose ![]() and
and ![]() are continuous, nonnegative functions such that
are continuous, nonnegative functions such that ![]() for
for ![]() Let
Let ![]() denote the region bounded on the right by the graph of
denote the region bounded on the right by the graph of ![]() on the left by the graph of
on the left by the graph of ![]() below by the line
below by the line ![]() and above by the line
and above by the line ![]() Then, the volume of the solid of revolution formed by revolving
Then, the volume of the solid of revolution formed by revolving ![]() around the y-axis is given by
around the y-axis is given by
![Rendered by QuickLaTeX.com \ds V=\int\limits_{c}^{d}\pi \left[{(u(y))}^{2}-{(v(y))}^{2}\right]dy.](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-8919f63a7c84698f696f60e83407bd7c_l3.png)
Rather than looking at an example of the washer method with the y-axis as the axis of revolution, we now consider an example in which the axis of revolution is a line other than one of the two coordinate axes. The same general method applies, but you may have to visualize just how to describe the cross-sectional area of the volume.
The Washer Method with a Different Axis of Revolution
Find the volume of a solid of revolution formed by revolving the region bounded above by ![]() and below by the x-axis. over the interval
and below by the x-axis. over the interval ![]() around the line
around the line ![]()
Solution
The graph of the region and the solid of revolution are shown in the following figure.
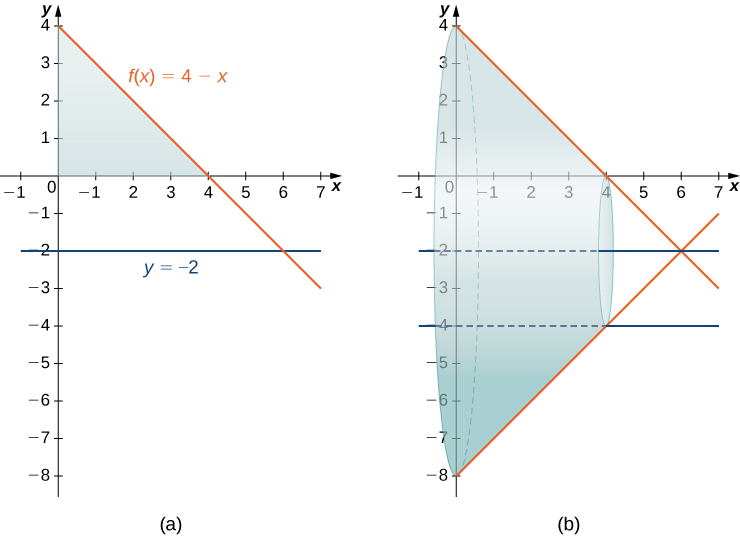
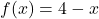 and the x-axis over the interval
and the x-axis over the interval ![Rendered by QuickLaTeX.com \ds \left[0,4\right].](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-47cf87a8ffe975c087ef1c3f08a74e57_l3.png) (b) Revolving the region about the line
(b) Revolving the region about the line  generates a solid of revolution with a cylindrical hole through its middle.
generates a solid of revolution with a cylindrical hole through its middle.We can’t apply the volume formula to this problem directly because the axis of revolution is not one of the coordinate axes. However, we still know that the area of the cross-section is the area of the outer circle less the area of the inner circle. Looking at the graph of the function, we see the radius of the outer circle is given by ![]() which simplifies to
which simplifies to
The radius of the inner circle is ![]() Therefore, we have
Therefore, we have
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill V&\ds =\int\limits_{0}^{4}\pi \left[{(6-x)}^{2}-{(2)}^{2}\right]\,dx \hfill \\[5mm]\ds &\ds =\pi \int\limits_{0}^{4}({x}^{2}-12x+32)\,dx \text{}={\pi \left[\frac{{x}^{3}}{3}-6{x}^{2}+32x\right]}\Big|_{0}^{4}=\frac{160\pi }{3}\ {\text{units}}^{3}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-15496ae2aaf7e40e3baded388d5d9386_l3.png)
Find the volume of a solid of revolution formed by revolving the region bounded above by the graph of ![]() and below by the x-axis over the interval
and below by the x-axis over the interval ![]() around the line
around the line ![]()
Answer
![]() units 3
units 3
Key Concepts
- Definite integrals can be used to find the volumes of solids. Using the slicing method, we can find a volume by integrating the cross-sectional area.
- For solids of revolution, the volume slices are often disks and the cross-sections are circles. The method of disks involves applying the method of slicing in the particular case in which the cross-sections are circles, and using the formula for the area of a circle.
- If a solid of revolution has a cavity in the center, the volume slices are washers. With the method of washers, the area of the inner circle is subtracted from the area of the outer circle before integrating.
Key Equations
- Disk Method along the x-axis
![Rendered by QuickLaTeX.com \ds V=\int\limits_{a}^{b}\pi {\left[f(x)\right]}^{2}\,dx](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-4696a77975e4d92f47b6cf7773082d89_l3.png)
- Disk Method along the y-axis
![Rendered by QuickLaTeX.com \ds V=\int\limits_{c}^{d}\pi {\left[g(y)\right]}^{2}dy](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-ea188485763865cdfc8aa4aa3bbecdaf_l3.png)
- Washer Method
![Rendered by QuickLaTeX.com \ds V=\int\limits_{a}^{b}\pi \left[{(f(x))}^{2}-{(g(x))}^{2}\right]\,dx](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7b3e1c7a9ad4e8e679ac854a7980dc2f_l3.png)
Exercises
1. Derive the formula for the volume of a sphere using the slicing method.
2. Use the slicing method to derive the formula for the volume of a cone.
3. Use the slicing method to derive the formula for the volume of a regular tetrahedron with side length ![]()
4. Explain when you would use the disk method versus the washer method. When are they interchangeable?
For the following exercises, draw a typical slice and find the volume using the slicing method for the given volume.
5. A pyramid with height 6 units and square base of side 2 units, as pictured here.

Answer
8 units 3
6. A pyramid with height 4 units and a rectangular base with length 2 units and width 3 units, as pictured here.

7. A regular tetrahedron with a side of 4 units, as seen here.

Answer
![]() units 3
units 3
8. A pyramid with height 5 units, and an isosceles triangular base with lengths of 6 units and 8 units, as seen here.

9. A cone of radius ![]() and height
and height ![]() has a smaller cone of radius
has a smaller cone of radius ![]() and height
and height ![]() removed from the top, as seen here. The resulting solid is called a frustum .
removed from the top, as seen here. The resulting solid is called a frustum .

Answer
![]() units 3
units 3
For the following exercises, draw an outline of the solid and find the volume using the slicing method.
10. The base is a circle of radius ![]() The slices perpendicular to the base are squares.
The slices perpendicular to the base are squares.
11. The base is a triangle with vertices ![]() and
and ![]() Slices perpendicular to the x-axis are semicircles.
Slices perpendicular to the x-axis are semicircles.
Answer

![]() units 3
units 3
12. The base is the region under the parabola ![]() in the first quadrant. Slices perpendicular to the x-axis are squares.
in the first quadrant. Slices perpendicular to the x-axis are squares.
13. The base is the region under the parabola ![]() and above the x-axis. Slices perpendicular to the y-axis are squares.
and above the x-axis. Slices perpendicular to the y-axis are squares.
Answer

2 units 3
14. The base is the region enclosed by ![]() and
and ![]() Slices perpendicular to the x-axis are right isosceles triangles with the hypotenuse in the base.
Slices perpendicular to the x-axis are right isosceles triangles with the hypotenuse in the base.
15. The base is the area between ![]() and
and ![]() Slices perpendicular to the x-axis are semicircles.
Slices perpendicular to the x-axis are semicircles.
Answer

![]() units 3
units 3
For the following exercises, draw the region bounded by the curves. Then, use the disk or the washer method to find the volume when the region is rotated around the given horizontal axis.
16. ![]() , rotated around the x-axis
, rotated around the x-axis
17. ![]() , rotated around the x-axis
, rotated around the x-axis
Answer

![]() units 3
units 3
18. ![]() , rotated around the x-axis
, rotated around the x-axis
19. ![]() in quadrant I, rotated around the line
in quadrant I, rotated around the line ![]()
Answer

![]() units 3
units 3
20. ![]() , rotated around the line
, rotated around the line ![]()
21. ![]() (in the first quadrant), rotated around the
(in the first quadrant), rotated around the ![]() -axis
-axis
(Hint: use the formula ![]() )
)
Answer

![]() units 3
units 3
22. ![]() , rotated around the line
, rotated around the line ![]()
23. ![]() , rotated around the x-axis
, rotated around the x-axis
Answer

![]() units 3
units 3
For the following exercises, draw the region bounded by the curves. Then, find the volume when the region is rotated around the y-axis.
24. ![]()
25. ![]()
Answer

![]() units 3
units 3
26. ![]() in quadrant I
in quadrant I
27. ![]()
Answer

![]() units 3
units 3
28. ![]()
29. ![]()
Answer

![]() units 3
units 3
30. ![]()
31. ![]()
Answer

![]() units 3
units 3
For the following exercises, draw the region bounded by the curves. Then, find the volume when the region is rotated around the given horizontal axis.
32. ![]() , rotated around the line
, rotated around the line ![]()
33. ![]() , rotated around the line
, rotated around the line ![]()
Answer
![]() units 3
units 3
34. ![]() , rotated around the x-axis
, rotated around the x-axis
35. ![]() , rotated around the line
, rotated around the line ![]()
Answer

![]() units 3
units 3
36. [T] ![]() , rotated around the x-axis
, rotated around the x-axis
37. ![]() , rotated around the line
, rotated around the line ![]()
Answer
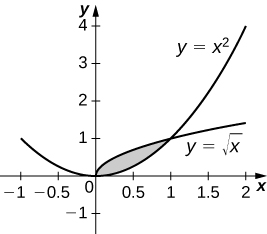
![]() units 3
units 3
38. ![]() , rotated around the x-axis
, rotated around the x-axis
(Hint: use the formula ![]() )
)
39. ![]() , rotated around the x-axis
, rotated around the x-axis
Answer

![]() units 3
units 3
For the following exercises, draw the region bounded by the curves. Then, use the washer method to find the volume when the region is revolved around the given vertical line.
40. ![]() , rotated around the line
, rotated around the line ![]()
41. ![]() , rotated around the y-axis
, rotated around the y-axis
Answer

![]() units 3
units 3
42. ![]() ,
, ![]() , and
, and ![]() , rotated around the line
, rotated around the line ![]()
43. ![]() , rotated around the y-axis
, rotated around the y-axis
Answer

![]() units 3
units 3
44. ![]() , rotated around the line
, rotated around the line ![]() .
.
45. Yogurt containers can be shaped like frustums. Rotate the line ![]() around the y-axis to find the volume between
around the y-axis to find the volume between ![]()

Answer
![]() units 3
units 3
46. Rotate the ellipse ![]() around the x-axis to approximate the volume of a football, as seen here.
around the x-axis to approximate the volume of a football, as seen here.

47. Rotate the ellipse ![]() around the y-axis to approximate the volume of a football.
around the y-axis to approximate the volume of a football.
Answer
![]() units 3
units 3
48. A better approximation of the volume of a football is given by the solid that comes from rotating ![]() around the x-axis from
around the x-axis from ![]() to
to ![]() What is the volume of this football approximation, as seen here?
What is the volume of this football approximation, as seen here?

49. What is the volume of the Bundt cake that comes from rotating ![]() around the y-axis from
around the y-axis from ![]() to
to ![]()

Answer
![]() units 3
units 3
For the following exercises, find the volume of the solid described.
50. The base is the region between ![]() and
and ![]() Slices perpendicular to the x-axis are semicircles.
Slices perpendicular to the x-axis are semicircles.
51. The base is the region enclosed by the generic ellipse ![]() Slices perpendicular to the x-axis are semicircles.
Slices perpendicular to the x-axis are semicircles.
Answer
![]() units 3
units 3
52. Bore a hole of radius ![]() down the axis of a right cone and through the base of radius
down the axis of a right cone and through the base of radius ![]() as seen here.
as seen here.

53. Find the volume common to two spheres of radius ![]() with centers that are
with centers that are ![]() apart, as shown here.
apart, as shown here.

Answer
![]() units 3
units 3
54. Find the volume of a spherical cap of height ![]() and radius
and radius ![]() where
where ![]() as seen here.
as seen here.

55. Find the volume of a sphere of radius ![]() with a cap of height
with a cap of height ![]() removed from the top, as seen here.
removed from the top, as seen here.

Answer
![]() units 3
units 3
Glossary
- cross-section
- the intersection of a plane and a solid object
- disk method
- a special case of the slicing method used with solids of revolution when the slices are disks
- slicing method
- a method of calculating the volume of a solid that involves cutting the solid into pieces, estimating the volume of each piece, then adding these estimates to arrive at an estimate of the total volume; as the number of slices goes to infinity, this estimate becomes an integral that gives the exact value of the volume
- solid of revolution
- a solid generated by revolving a region in a plane around a line in that plane
- washer method
- a special case of the slicing method used with solids of revolution when the slices are washers


Hint
Use similar triangles, as in the example above.