0.3 L’Hôpital’s Rule
Learning Objectives
-
Recognize when to apply L’Hôpital’s rule.
-
Identify indeterminate forms produced by quotients, products, differences, and powers, and apply L’Hôpital’s rule in each case.
-
Describe the relative growth rates of functions.
In this section, we examine a powerful tool for evaluating limits. This tool, known as L’Hôpital’s rule, uses derivatives to calculate limits. With this rule, we will be able to evaluate many limits we have not yet been able to determine. Instead of relying on numerical evidence to conjecture that a limit exists, we will be able to show definitively that a limit exists and to determine its exact value.
Applying L’Hôpital’s Rule
L’Hôpital’s rule can be used to evaluate limits involving the quotient of two functions. Consider ![]()
If ![]() then
then ![]()
However, what happens if ![]() In this case, we have to deal with what’s called the indeterminate form of type
In this case, we have to deal with what’s called the indeterminate form of type ![]() The form is indeterminate because we cannot determine the exact behavior of the quotient
The form is indeterminate because we cannot determine the exact behavior of the quotient ![]() as
as ![]() approaches
approaches ![]() without further analysis.
without further analysis.
For example, consider the limits ![]() The first limit can be evaluated by factoring the numerator:
The first limit can be evaluated by factoring the numerator:
![]()
As for ![]() , one can use a geometric argument to show that
, one can use a geometric argument to show that ![]()
Note that although both limits we just considered exist, in fact, anything is possible for the indeterminate form: the limit might exist and be equal to any real number ![]() , the limit might not exist, but there might be a trend of
, the limit might not exist, but there might be a trend of ![]() or
or ![]() , or there might be no limit and no trend. For example, knowing that
, or there might be no limit and no trend. For example, knowing that ![]() , it is easy to show that
, it is easy to show that ![]()
We are going to develop a universal technique for evaluating limits such as the ones above. Not only does it allow for an alternative and sometimes easier way to evaluate these limits, but also, and more importantly, it works for evaluating many other limits that we could not calculate before.
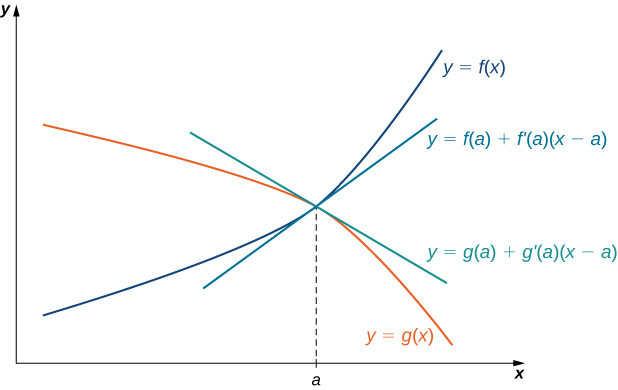
The idea behind L’Hôpital’s rule can be explained using local linear approximations. Consider two differentiable functions ![]() and
and ![]() such that
such that ![]() and
and ![]() . For
. For ![]() that is very close to
that is very close to ![]() we can write
we can write ![]() and
and ![]() (This follows either from the geometric understanding that the tangent line is very close to the graph around the point where the tangent “touches” the curve or, algebraically, from the formal limit definition of the derivative.)
(This follows either from the geometric understanding that the tangent line is very close to the graph around the point where the tangent “touches” the curve or, algebraically, from the formal limit definition of the derivative.)
Therefore, ![]()
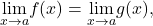 then the ratio
then the ratio 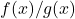 is approximately equal to the ratio of their linear approximations near
is approximately equal to the ratio of their linear approximations near 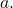
Since ![]() is differentiable at
is differentiable at ![]() it is continuous at
it is continuous at ![]() and therefore
and therefore ![]() Similarly,
Similarly, ![]() If we also assume that
If we also assume that ![]() and
and ![]() are continuous at
are continuous at ![]() then
then ![]() and
and ![]() Using these arguments, we conclude that
Using these arguments, we conclude that
![]()
Note that the assumptions that ![]() and
and ![]() are continuous at
are continuous at ![]() and
and ![]() can be loosened. We state L’Hôpital’s rule formally for the indeterminate form
can be loosened. We state L’Hôpital’s rule formally for the indeterminate form ![]() Also note that writing
Also note that writing ![]() does not mean we are actually dividing zero by zero. It is just the notation we use when dealing with a limit of a quotient with both numerator and denominator approaching zero.
does not mean we are actually dividing zero by zero. It is just the notation we use when dealing with a limit of a quotient with both numerator and denominator approaching zero.
L’Hôpital’s Rule (  Case)
Case)
Suppose ![]() and
and ![]() are differentiable functions over an open interval containing
are differentiable functions over an open interval containing ![]() except possibly at
except possibly at ![]() If
If ![]() and
and ![]() then
then
Proof
We provide a proof of this theorem in the special case when ![]() and
and ![]() are all continuous over an open interval containing
are all continuous over an open interval containing ![]() In this case, since
In this case, since ![]() and
and ![]() and
and ![]() are continuous at
are continuous at ![]() we have that
we have that ![]() Therefore,
Therefore,
![Rendered by QuickLaTeX.com \begin{array}{ccc}\hfill \underset{x\to a}{\text{lim}}\ds\,\frac{f(x)}{g(x)}& =\underset{x\to a}{\text{lim}}\ds\,\frac{f(x)-f(a)}{g(x)-g(a)}\hfill & \quad\text{since}\ f(a)=0=g(a)\hfill \\[5mm] & =\underset{x\to a}{\text{lim}}\ds\,\frac{\ds\,\frac{f(x)-f(a)}{x-a}}{\ds\,\frac{g(x)-g(a)}{x-a}}\hfill & \quad \text{algebra}\hfill\\[5mm] & =\displaystyle \frac{\underset{x\to a}{\text{lim}}\ds\,\frac{f(x)-f(a)}{x-a}}{\underset{x\to a}{\text{lim}}\ds\,\frac{g(x)-g(a)}{x-a}}\hfill & \quad \text{limit of a quotient}\hfill\\[5mm] & \ds=\,\frac{{f}^{\prime }(a)}{{g}^{\prime }(a)}\hfill & \quad \text{definition of the derivative}\hfill \\[5mm] & =\ds\,\frac{\underset{x\to a}{\text{lim}}{f}^{\prime }(x)}{\underset{x\to a}{\text{lim}}{g}^{\prime }(x)}\hfill & \quad \text{continuity of}\ {f}^{\prime }\text{ and }{g}^{\prime }\hfill \\[5mm] & =\underset{x\to a}{\text{lim}}\ds\,\frac{{f}^{\prime }(x)}{{g}^{\prime }(x)}.\hfill & \quad \text{limit of a quotient}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-35dc78d4c433e7df027c4a4f276c6c57_l3.png)
Note that L’Hôpital’s rule allows to calculate the limit of a quotient ![]() by considering the limit of the quotient of the derivatives
by considering the limit of the quotient of the derivatives ![]() It is important to realize that we are not calculating the derivative of the quotient
It is important to realize that we are not calculating the derivative of the quotient ![]()
Applying L’Hôpital’s Rule (  Case)
Case)
Evaluate each of the following limits using L’Hôpital’s rule.
Solution
-
Since the numerator
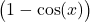 approaches
approaches 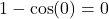 and the denominator
and the denominator 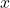 approaches 0 when
approaches 0 when 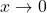 , we can apply L’Hôpital’s rule to evaluate this limit. We have
, we can apply L’Hôpital’s rule to evaluate this limit. We have![Rendered by QuickLaTeX.com \begin{array}{cc}\hfill \underset{x\to 0}{\text{lim}}\ds\,\frac{1- \cos (x)}{x}& =\underset{x\to 0}{\text{lim}}\ds\,\frac{\ds\,\big(1- \cos (x)\big)'}{\ds\,(x)'}=\underset{x\to 0}{\text{lim}}\ds\,\frac{ \sin (x)}{1}\hfill \\[5mm] \hfill &=\ds\,\frac{\underset{x\to 0}{\text{lim}}\,\sin (x)}{\underset{x\to 0}{\text{lim}}1}=\,\frac{\sin(0)}1=\ds\,\frac{0}{1}=0.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-909baf5a0328cbd1aca88f1697ec26e9_l3.png)
-
As
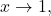
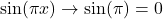 and
and 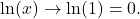 Therefore, we can apply L’Hôpital’s rule. We obtain
Therefore, we can apply L’Hôpital’s rule. We obtain![Rendered by QuickLaTeX.com \begin{array}{cc}\hfill \underset{x\to 1}{\text{lim}}\ds\,\frac{ \sin (\pi x)}{\text{ln}(x)}&=\underset{x\to 1}{\text{lim}}\ds\,\frac{ \big(\sin (\pi x)\big)'}{\big(\text{ln}(x)\big)'} =\underset{x\to 1}{\text{lim}}\ds\,\frac{\cos (\pi x)\cdot \pi}{1\text{/}x}\hfill \\[5mm] & =\ds\frac\,{\cos(\pi)\cdot\pi}{1/1}=(-1)\pi=-\pi .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-3019d06a817ebb851d1a7e2eaa2501b3_l3.png)
-
When
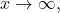 we have that
we have that 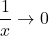 , that is, the denominator approaches 0, and the numerator
, that is, the denominator approaches 0, and the numerator 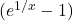 approaches
approaches 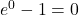 . Therefore, we can apply L’Hôpital’s rule. We obtain
. Therefore, we can apply L’Hôpital’s rule. We obtain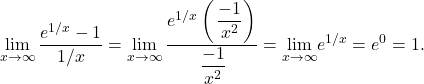
-
As
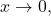 both numerator and denominator approach zero:
both numerator and denominator approach zero: 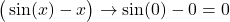 and
and 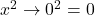 . Therefore, we can apply L’Hôpital’s rule. We obtain
. Therefore, we can apply L’Hôpital’s rule. We obtain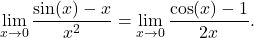
Since numerator and denominator of this new quotient both approach 0 as
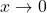
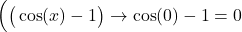 and
and 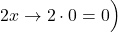 , we apply L’Hôpital’s rule again. In doing so, we see that
, we apply L’Hôpital’s rule again. In doing so, we see that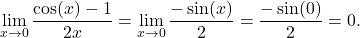
Therefore, we conclude that
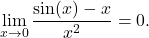
Evaluate ![]()
Answer
-1
We can also use L’Hôpital’s rule to evaluate limits of quotients ![]() in which
in which ![]() and
and ![]() Limits of this form are classified as indeterminate forms of type
Limits of this form are classified as indeterminate forms of type ![]() Again, note that we are not actually dividing
Again, note that we are not actually dividing ![]() by
by ![]() Since
Since ![]() is not a real number, that is impossible; rather,
is not a real number, that is impossible; rather, ![]() is the notation we use when dealing with a limit of a quotient with both numerator and denominator having an infinite trend of
is the notation we use when dealing with a limit of a quotient with both numerator and denominator having an infinite trend of ![]() or
or ![]() .
.
L’Hôpital’s Rule (  Case)
Case)
Suppose that ![]() and
and ![]() are differentiable functions over an open interval containing
are differentiable functions over an open interval containing ![]() except possibly at
except possibly at ![]() Further suppose that
Further suppose that ![]() and
and ![]() Then,
Then,
![]() provided that the limit on the right exists or has a trend of
provided that the limit on the right exists or has a trend of ![]() or
or ![]() This result also holds for one-sided limits or if the finite number
This result also holds for one-sided limits or if the finite number ![]() is replaced with
is replaced with ![]() or
or ![]()
Applying L’Hôpital’s Rule (  Case)
Case)
Evaluate each of the following limits using L’Hôpital’s rule.
Solution
-
Since
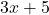 and
and 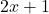 are first-degree polynomials with positive leading coefficients,
are first-degree polynomials with positive leading coefficients, 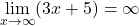 and
and 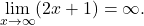 Therefore, we apply L’Hôpital’s rule and obtain
Therefore, we apply L’Hôpital’s rule and obtain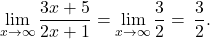
Note that this limit can also be calculated without invoking L’Hôpital’s rule, by dividing the numerator and denominator by the highest power of
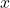 in the denominator:
in the denominator: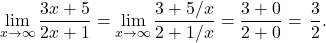
L’Hôpital’s rule provides us with an alternative means of evaluating limits of this type.
-
Here,
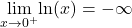 and
and 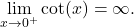 Therefore, we can apply L’Hôpital’s rule and obtain
Therefore, we can apply L’Hôpital’s rule and obtain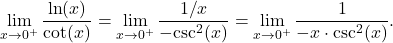
Now, as
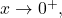
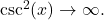 Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In this case, anything can happen to the product, and we cannot make any conclusion yet. (Actually, this is an indeterminate form
Therefore, the first term in the denominator is approaching zero and the second term is getting really large. In this case, anything can happen to the product, and we cannot make any conclusion yet. (Actually, this is an indeterminate form 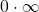 that will be discussed a bit later.) To evaluate the limit, we use the relation of
that will be discussed a bit later.) To evaluate the limit, we use the relation of 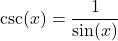 to rewrite the quotient under the limit:
to rewrite the quotient under the limit: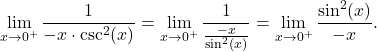
Now,
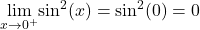 and
and 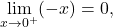 so we can apply L’Hôpital’s rule again:
so we can apply L’Hôpital’s rule again: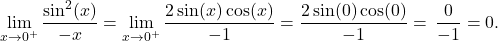
We conclude that
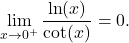
Evaluate ![]()
Answer
0
As was already mentioned, L’Hôpital’s rule is an extremely useful tool for evaluating limits. It is important to remember, however, that to apply L’Hôpital’s rule to a quotient ![]() it is essential that the limit of
it is essential that the limit of ![]() be of the form
be of the form ![]() or
or ![]() This will be illustrated in the example below.
This will be illustrated in the example below.
When L’Hôpital’s Rule Does Not Apply
Consider ![]() Show that the limit cannot be evaluated by applying L’Hôpital’s rule.
Show that the limit cannot be evaluated by applying L’Hôpital’s rule.
Solution
Because the limits of the numerator and denominator are not both zero and are not both infinite, we cannot apply L’Hôpital’s rule. If we tried to do so, we would have erroneously concluded that
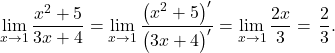
However, since ![]() and
and ![]() using the arithmetic properties of limits, we actually have that
using the arithmetic properties of limits, we actually have that ![]() and so that
and so that
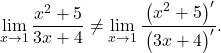
Another, trickier, case when L’Hôpital’s rule cannot be applied is when the limit of the quotient obtained after differentiation does not exist. Indeed, if we carefully read the statements of the L’Hôpital’s rule theorems, we can notice that they both say “provided that the limit on the right ![]() exists”. We explore the situation when this condition fails in the next example.
exists”. We explore the situation when this condition fails in the next example.
When L’Hôpital’s Rule Does Not Apply
Consider ![]() Show that the limit cannot be evaluated by applying L’Hôpital’s rule.
Show that the limit cannot be evaluated by applying L’Hôpital’s rule.
Solution
Both numerator and denominator approach infinity. Thus it appears that we can apply L’Hôpital’s rule. If we tried to do so, we would have erroneously concluded that
![]()
However, since ![]() neither exists, nor is infinite, L’Hôpital’s rule does not actually apply.
neither exists, nor is infinite, L’Hôpital’s rule does not actually apply.
Note that this does not mean that the original limit fails to exist. Because ![]() , when
, when ![]() , we have that
, we have that
![]() . Now since
. Now since
![]() (that can be proved using L’Hôpital’s rule), we can use the squeeze theorem to conclude that
(that can be proved using L’Hôpital’s rule), we can use the squeeze theorem to conclude that ![]()
Explain why we cannot apply L’Hôpital’s rule to evaluate ![]() Evaluate
Evaluate ![]() by other means.
by other means.
Answer
![]()
Other Indeterminate Forms
We have seen that L’Hôpital’s rule is very useful for dealing with the indeterminate forms ![]() and
and ![]() . It can also help to evaluate limits involving other indeterminate forms such as
. It can also help to evaluate limits involving other indeterminate forms such as ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . As before, these expressions should be treated not as algebraic operations but as the notation reflecting the behavior of the function under the limit. We show why they are indeterminate forms and how to use L’Hôpital’s rule to evaluate the corresponding limits. The key idea is to rewrite the expression as a quotient of the form
. As before, these expressions should be treated not as algebraic operations but as the notation reflecting the behavior of the function under the limit. We show why they are indeterminate forms and how to use L’Hôpital’s rule to evaluate the corresponding limits. The key idea is to rewrite the expression as a quotient of the form ![]() or
or ![]() .
.
Indeterminate Form of Type 
Suppose we want to evaluate ![]() , where
, where ![]() and
and ![]() as
as ![]() . Since one term in the product is approaching zero but the other term is becoming arbitrarily large in magnitude, anything can happen to the product. We use the notation
. Since one term in the product is approaching zero but the other term is becoming arbitrarily large in magnitude, anything can happen to the product. We use the notation ![]() to denote the form that arises in this situation. The expression
to denote the form that arises in this situation. The expression ![]() is considered indeterminate because, without further analysis, we cannot determine the exact behavior of the product
is considered indeterminate because, without further analysis, we cannot determine the exact behavior of the product ![]() as
as ![]() .
.
For example, let n be a positive integer and consider ![]() . As
. As ![]() ,
, ![]() and
and ![]() . However, the limit of
. However, the limit of ![]() as
as ![]() varies, depending on
varies, depending on ![]() . Indeed,
. Indeed,
if ![]() , then
, then ![]() ,
,
if ![]() , then
, then ![]() ,
,
and if ![]() , then
, then ![]() . (All these limits can be evaluated by either dividing both numerator and denominator by the highest power of
. (All these limits can be evaluated by either dividing both numerator and denominator by the highest power of ![]() in the denominator or by using L’Hôpital’s rule, multiple times, when needed).
in the denominator or by using L’Hôpital’s rule, multiple times, when needed).
We now consider another limit involving the indeterminate form ![]() and show how to rewrite the function as a quotient to use L’Hôpital’s rule.
and show how to rewrite the function as a quotient to use L’Hôpital’s rule.
Indeterminate Form of Type 
Evaluate ![]()
Solution
To be able to use L’Hôpital’s rule, we rewrite the function ![]() as a quotient in the following way:
as a quotient in the following way: ![]() . Since
. Since ![]() as
as ![]() and
and ![]() as
as ![]() , we can apply L’Hôpital’s rule to obtain
, we can apply L’Hôpital’s rule to obtain
![]()
We conclude that ![]()
In general, one of the ways to transform a product of functions ![]() into a quotient is to use double reciprocals, that is, rewrite
into a quotient is to use double reciprocals, that is, rewrite ![]() as
as ![]() or
or ![]() .
.
Evaluate ![]()
Answer
1
Indeterminate Form of Type 
Suppose that ![]() (or
(or ![]() ). Then the limit
). Then the limit ![]() represents an indeterminate form
represents an indeterminate form ![]() .
.
To show that this is, indeed, an indeterminate form, and the answer could be anything, consider the following example. Let ![]() be a positive integer,
be a positive integer, ![]() and
and ![]() . As
. As ![]() ,
, ![]() and
and ![]() , but
, but ![]() depends on the value of the exponent
depends on the value of the exponent ![]() . To see this, we recall that, when
. To see this, we recall that, when ![]() , the behavior of a polynomial
, the behavior of a polynomial ![]()
![]() is determined by the leading term
is determined by the leading term ![]() since
since ![]() and
and ![]() for any
for any ![]() .
.
Therefore, if ![]() , then
, then ![]() .
.
On the other hand, if ![]() , then
, then ![]() .
.
Finally, if ![]() , then
, then ![]() .
.
In the next example, we show how to rewrite an expression involving the indeterminate form ![]() as a fraction in order to apply L’Hôpital’s rule.
as a fraction in order to apply L’Hôpital’s rule.
Indeterminate Form of Type 
Evaluate ![]()
Solution
Bringing the expression to a common denominator, we obtain
![]()
Since ![]() and
and ![]() , we can apply L’Hôpital’s rule.
, we can apply L’Hôpital’s rule.
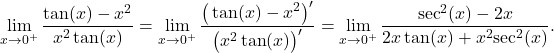
We have that ![]() and
and ![]() Because the denominator is positive as
Because the denominator is positive as ![]() approaches zero from the right, we conclude that
approaches zero from the right, we conclude that ![]()
Therefore, ![]()
In general, bringing the difference of fractions to a common denominator often works to reduce an ![]() indeterminate form to
indeterminate form to ![]() or
or ![]() form, after which L’Hôpital’s rule can be applied.
form, after which L’Hôpital’s rule can be applied.
Evaluate ![]()
Answer
0
Hint
Rewrite the difference of fractions as a single fraction.
Another types of indeterminate forms that arise when evaluating limits involve exponents. The expressions ![]()
![]() and
and ![]() are all indeterminate forms. Again, these expressions are not meant to be evaluated using algebraic operations, rather they provide a notation used to describe the behavior of a function under the limit. We now demonstrate how L’Hôpital’s rule can be used to evaluate limits involving these indeterminate forms.
are all indeterminate forms. Again, these expressions are not meant to be evaluated using algebraic operations, rather they provide a notation used to describe the behavior of a function under the limit. We now demonstrate how L’Hôpital’s rule can be used to evaluate limits involving these indeterminate forms.
Suppose we want to evaluate ![]() and we arrive at one of the indeterminate forms listed above. We proceed as follows. Let
and we arrive at one of the indeterminate forms listed above. We proceed as follows. Let ![]() Then,
Then, ![]() and we first evaluate
and we first evaluate ![]() . This allows to reduce an indeterminate power to an indeterminate product. Indeed,
. This allows to reduce an indeterminate power to an indeterminate product. Indeed, ![]() corresponds to
corresponds to ![]() ,
, ![]() corresponds to
corresponds to ![]() , and
, and ![]() corresponds to
corresponds to ![]() . We then use the techniques discussed earlier to rewrite the expression
. We then use the techniques discussed earlier to rewrite the expression ![]() as a quotient so that we can apply L’Hôpital’s rule. Suppose that
as a quotient so that we can apply L’Hôpital’s rule. Suppose that ![]() where
where ![]() may be
may be ![]() or
or ![]() So we have that
So we have that ![]() and since the natural logarithm function is continuous, we conclude that
and since the natural logarithm function is continuous, we conclude that ![]() It follows that
It follows that ![]()
Indeterminate Form of Type 
Evaluate ![]()
Solution
Let ![]() Then
Then ![]()
We first need to evaluate ![]() Since both numerator and denominator approach infinity as
Since both numerator and denominator approach infinity as ![]() , we can apply L’Hôpital’s rule to obtain
, we can apply L’Hôpital’s rule to obtain ![]()
So we have that ![]() and since the natural logarithm function is continuous, we conclude that
and since the natural logarithm function is continuous, we conclude that ![]()
This leads to ![]()
Evaluate ![]()
Answer
![]()
Hint
Take ![]() and consider
and consider ![]() .
.
Indeterminate Form of Type 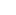
Evaluate ![]()
Solution
Let ![]() Then
Then ![]()
We now evaluate ![]() Since
Since ![]() and
and ![]() we have the indeterminate form
we have the indeterminate form ![]() To apply L’Hôpital’s rule, we need to rewrite
To apply L’Hôpital’s rule, we need to rewrite ![]() as a fraction. We could write
as a fraction. We could write
![]() or
or ![]()
Let’s consider the first option. In this case, applying L’Hôpital’s rule, we would obtain
![Rendered by QuickLaTeX.com \begin{array}{ll}\ds\underset{x\to {0}^{+}}{\text{lim}} \sin (x)\text{ln}(x)&=\underset{x\to {0}^{+}}{\text{lim}}\ds\,\frac{ \sin (x)}{1\text{/}\text{ln}(x)}=\underset{x\to {0}^{+}}{\text{lim}}\ds\,\frac{ \cos (x)}{\big(-1\text{/}{(\text{ln}(x))}^{2}\big)\cdot1\text{/}x}\\[5mm]&=\underset{x\to {0}^{+}}{\text{lim}}(-x{(\text{ln}(x))}^{2} \cos (x)).\end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-e561121931356d60f52c31f0dc2a9074_l3.png)
Unfortunately, we not only have another expression involving the indeterminate form ![]() but the new limit is even more complicated to evaluate than the one we started with. Instead, we try the second option. By writing
but the new limit is even more complicated to evaluate than the one we started with. Instead, we try the second option. By writing ![]() and applying L’Hôpital’s rule, we obtain
and applying L’Hôpital’s rule, we obtain
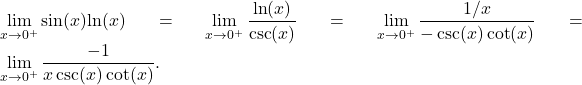
Using the fact that ![]() and
and ![]() we can rewrite the last limit as
we can rewrite the last limit as
![]()
Because ![]() , we can apply L’Hôpital’s rule again to get
, we can apply L’Hôpital’s rule again to get
![Rendered by QuickLaTeX.com \begin{array}{ll}\underset{x\to {0}^{+}}{\text{lim}}\ds\,\frac{-{ \sin }(x)\tan(x)}{x}&=\lim\limits_{x\to0^+}\,\dfrac{-\cos(x)\tan(x)-\sin(x)\sec^2(x)}{1}\\[5mm]&=\dfrac{-1\cdot0-0\cdot1}{1}=0.\end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-9734b99e97b4b6c8620c6ef1dcf2851f_l3.png)
We conclude that ![]() Using the continuity of logarithmic function, we obtain that
Using the continuity of logarithmic function, we obtain that ![]() , and hence
, and hence
Evaluate ![]()
Answer
1
Hint
Take ![]() and consider
and consider ![]() .
.
Growth Rates of Functions
Suppose the functions ![]() and
and ![]() both approach infinity as
both approach infinity as ![]() Although the values of both functions become arbitrarily large as the values of
Although the values of both functions become arbitrarily large as the values of ![]() become sufficiently large, sometimes one function is growing more quickly than the other. For example,
become sufficiently large, sometimes one function is growing more quickly than the other. For example, ![]() and
and ![]() both approach infinity as
both approach infinity as ![]() However, as shown in the following table, the values of
However, as shown in the following table, the values of ![]() are growing much faster than the values of
are growing much faster than the values of ![]()
| |
10 | 100 | 1000 | 10,000 |
| |
100 | 10,000 | 1,000,000 | 100,000,000 |
| |
1000 | 1,000,000 | 1,000,000,000 |
In fact, ![]()
As a result, we say ![]() is growing more rapidly than
is growing more rapidly than ![]() as
as ![]() On the other hand, for
On the other hand, for ![]() and
and ![]() although the values of
although the values of ![]() are always greater than the values of
are always greater than the values of ![]() for
for ![]() each value of
each value of ![]() is roughly three times the corresponding value of
is roughly three times the corresponding value of ![]() as
as ![]() as shown in the following table. In fact,
as shown in the following table. In fact,
| |
10 | 100 | 1000 | 10,000 |
| |
100 | 10,000 | 1,000,000 | 100,000,000 |
| |
341 | 30,401 | 3,004,001 | 300,040,001 |
In this case, we say that ![]() and
and ![]() are growing at the same rate as
are growing at the same rate as ![]()
More generally, suppose ![]() and
and ![]() are two functions that approach infinity as
are two functions that approach infinity as ![]() We say
We say ![]() grows more rapidly than
grows more rapidly than ![]() as
as ![]() if
if
![]()
On the other hand, if there exist constants ![]() and a number
and a number ![]() such that
such that ![]() , for all
, for all ![]() , we say that
, we say that ![]() and
and ![]() grow at the same rate as
grow at the same rate as ![]() .
.
Next we see how to use L’Hôpital’s rule to compare the growth rates of power, exponential, and logarithmic functions.
Comparing the Growth Rates of  and
and 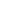
For each of the following pairs of functions, use L’Hôpital’s rule to evaluate ![]()
Solution
-
Since
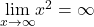 and
and 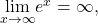 we can use L’Hôpital’s rule to evaluate
we can use L’Hôpital’s rule to evaluate 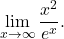 We obtain
We obtain 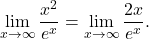
Because
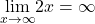 and
and 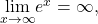 we can apply L’Hôpital’s rule again:
we can apply L’Hôpital’s rule again: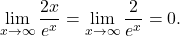
Hence,
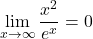 , which means that
, which means that 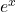 grows more rapidly than
grows more rapidly than 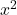 as
as 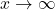 (see the figure with the graphs of these functions below).
(see the figure with the graphs of these functions below).
Figure 3. An exponential function grows at a faster rate than a power function. Growth rates of a power function and an exponential function. 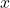
5 10 15 20 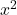
25 100 225 400 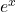
148 22,026 3,269,017 485,165,195 -
Since
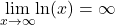 and
and 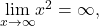 we can use L’Hôpital’s rule to evaluate
we can use L’Hôpital’s rule to evaluate 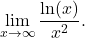 We obtain
We obtain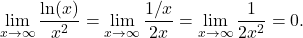
Thus,
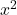 grows more rapidly than
grows more rapidly than 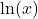 as
as 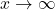 , which agrees with the following figure displaying the graphs of these functions.
, which agrees with the following figure displaying the graphs of these functions.
Figure 4. A power function grows at a faster rate than a logarithmic function. Growth rates of a power function and a logarithmic function 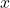
10 100 1000 10,000 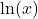
2.303 4.605 6.908 9.210 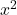
100 10,000 1,000,000 100,000,000
Compare the growth rates of ![]() and
and ![]()
Answer
The function ![]() grows faster than
grows faster than ![]()
Hint
Apply L’Hôpital’s rule sufficiently many times to evaluate ![]()
Using the same ideas as in example (a) above, it is not difficult to show that ![]() grows more rapidly than
grows more rapidly than ![]() for any
for any ![]() In the following table, we compare
In the following table, we compare ![]() with
with ![]() and
and ![]() as
as ![]() becomes large.
becomes large.
| |
5 | 10 | 15 | 20 |
| |
125 | 1000 | 3375 | 8000 |
| |
625 | 10,000 | 50,625 | 160,000 |
| |
148 | 22,026 | 3,269,017 | 485,165,195 |
Similarly, it is also easy to show that ![]() grows more rapidly than
grows more rapidly than ![]() for any
for any ![]() In the table below, we compare
In the table below, we compare ![]() with
with ![]() and
and ![]() when
when ![]() becomes large.
becomes large.
| |
10 | 100 | 1000 | 10,000 |
| |
2.303 | 4.605 | 6.908 | 9.210 |
| |
2.154 | 4.642 | 10 | 21.544 |
| |
3.162 | 10 | 31.623 | 100 |
Key Concepts
-
L’Hôpital’s rule can be used to evaluate the limit of a quotient when the indeterminate form
 or
or 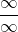 arises.
arises. -
L’Hôpital’s rule can also be applied to other indeterminate forms if the expressions under the limit can be rewritten as a quotient of indeterminate form
 or
or 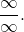
-
The exponential function
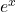 grows faster than any power function
grows faster than any power function 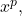
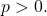
-
The logarithmic function
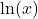 grows slower than any power function
grows slower than any power function 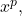
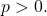
Exercises
For the following exercises, evaluate the given limit. If the limit does not exist, indicate whether there is a trend of ![]() or
or ![]() . In case you are using L’Hôpital’s rule, explain why it applies.
. In case you are using L’Hôpital’s rule, explain why it applies.
1. ![]()
Answer
![]()
2. ![]()
3. ![]()
Answer
![]()
4. ![]()
5. ![]()
Answer
![]()
6. ![]()
7. ![]()
Answer
-2
8. ![]()
9. ![]()
Answer
![]()
10. ![]()
11. ![]()
Answer
![]()
12. ![]()
13 ![]()
Answer
![]()
14. ![]()
15. ![]()
Answer
![]()
16. ![]() , where
, where ![]() is a fixed real number and
is a fixed real number and ![]() is a positive integer.
is a positive integer.
17. ![]()
Answer
![]()
18. ![]()
19. ![]()
Answer
![]()
20. ![]()
21. ![]()
Answer
![]()
22. ![]()
23. ![]()
Answer
![]()
24. ![]()
25. ![]()
Answer
1
26. ![]()
27. ![]()
Answer
0
28. ![]()
29. ![]()
Answer
![]()
30. ![]()
31. ![]()
Answer
![]()
32. ![]()
33. ![]()
Answer
1
34. ![]()
35. ![]()
Answer
![]()
36. ![]()
37. ![]()
Answer
![]()
38. ![]()
39. ![]()
Answer
![]()
41. ![]()
Answer
1
42. ![]()
43. ![]()
Answer
![]()
44. ![]()
45. ![]()
(Hint: Factor ![]() out of the expression.)
out of the expression.)
Answer
![]()
Glossary
- indeterminate forms
- when evaluating a limit, the forms
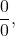
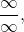
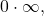
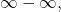
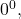
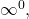 and
and 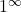 are considered indeterminate because further analysis is required to determine whether the limit exists and, if so, what its value is
are considered indeterminate because further analysis is required to determine whether the limit exists and, if so, what its value is
- L’Hôpital’s rule
- if
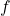 and
and 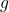 are differentiable functions over an open interval that contains
are differentiable functions over an open interval that contains 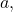 except possibly at
except possibly at 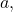 and
and 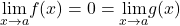 or
or 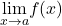 and
and 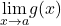 are infinite, then
are infinite, then 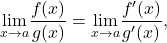 provided the limit on the right exists or has a trend of
provided the limit on the right exists or has a trend of 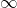 or
or 


Hint
Determine the limits of the numerator and denominator and analyze the behavior of the quotient.