7.4 Area and Arc Length in Polar Coordinates
Learning Objectives
- Derive the formula for area of a region in polar coordinates.
- Determine the arc length of a polar curve.
In the rectangular coordinate system, the definite integral provides a way to calculate the area under a curve. In particular, if we have a function ![]() defined from
defined from ![]() to
to ![]() where
where ![]() on this interval, the area between the curve and the x-axis is given by
on this interval, the area between the curve and the x-axis is given by 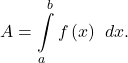 We can also find the arc length of this curve using the formula
We can also find the arc length of this curve using the formula 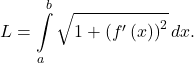 In this section, we study formulas for area and arc length in the polar coordinate system.
In this section, we study formulas for area and arc length in the polar coordinate system.
Areas of Regions Bounded by Polar Curves
Consider a polar curve defined by the function ![]() where
where ![]() We want to derive a formula for the area of the region bounded by the curve and between the radial lines
We want to derive a formula for the area of the region bounded by the curve and between the radial lines ![]() and
and ![]() , see Figure 1 below. When defining areas in rectangular coordinates, we approximated the regions with the union of rectangles, and here we are going to use sectors of a circle. Our first step is to partition the interval
, see Figure 1 below. When defining areas in rectangular coordinates, we approximated the regions with the union of rectangles, and here we are going to use sectors of a circle. Our first step is to partition the interval ![]() into n equal-width subintervals. The width of each subinterval is
into n equal-width subintervals. The width of each subinterval is ![]() and the ith partition point
and the ith partition point ![]() is given by the formula
is given by the formula ![]() Each partition point
Each partition point ![]() defines a line with slope
defines a line with slope ![]() passing through the pole as shown in the following graph.
passing through the pole as shown in the following graph.
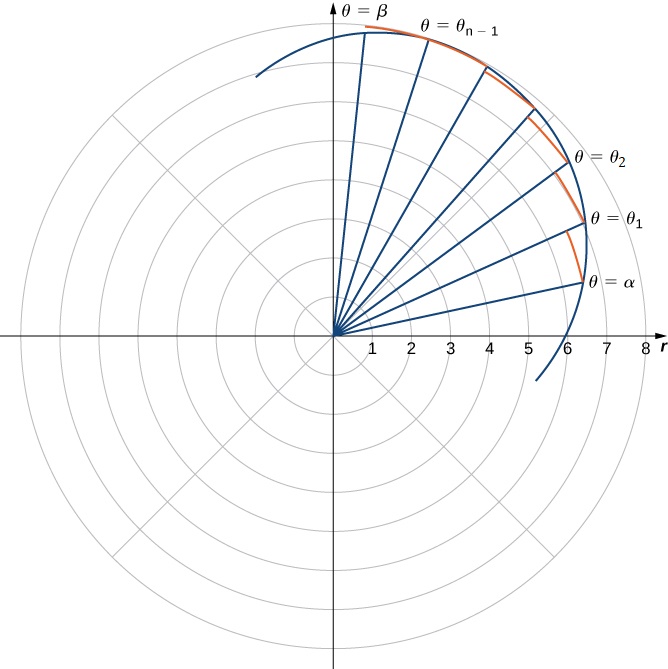
The line segments are connected by arcs of constant radius. This defines sectors whose areas can be calculated by using a geometric formula. The area of each sector is then used to approximate the area between successive line segments. We then sum the areas of the sectors to obtain a Riemann sum approximation for the total area. The formula for the area of a sector of a circle is illustrated in the following figure.
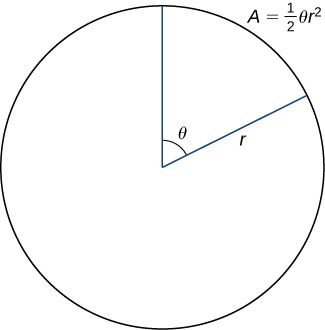
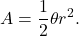
Recall that the area of a circle is ![]() A fraction of a circle can be measured by the central angle
A fraction of a circle can be measured by the central angle ![]() The full angle is
The full angle is ![]() , and so the fraction of the circle is given by
, and so the fraction of the circle is given by ![]() The area of the sector is this fraction multiplied by the total area:
The area of the sector is this fraction multiplied by the total area:
![]()
Since the radius of a typical sector in Figure 1 above is given by ![]() the area of the ith sector can be found as
the area of the ith sector can be found as
![]()
Summing the areas of sectors for ![]() , we obtain a Riemann sum that approximates the polar area:
, we obtain a Riemann sum that approximates the polar area:
![]()
We take the limit as ![]() to get the exact area:
to get the exact area:
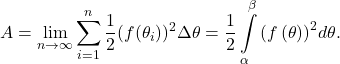
This gives the following theorem.
Area of a Region Bounded by a Polar Curve
Suppose ![]() is continuous and nonnegative on the interval
is continuous and nonnegative on the interval ![]() with
with ![]() The area of the region bounded by the graph of
The area of the region bounded by the graph of ![]() between the radial lines
between the radial lines ![]() and
and ![]() is
is
![Rendered by QuickLaTeX.com \ds (*)\quad A=\frac{1}{2}\int\limits_{\alpha }^{\beta }{\left[f\left(\theta \right)\right]}^{2}d\theta =\frac{1}{2}\int\limits_{\alpha }^{\beta }{r}^{2}d\theta .](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-ab1777ebcad7be582d848d66ac23d79c_l3.png)
Finding an Area of a Polar Region
Find the area of one petal of the rose defined by the equation ![]()
Solution
The graph of ![]() is shown below.
is shown below.
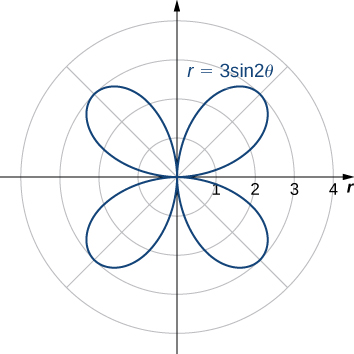
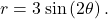
Each petal starts and ends at the pole, so to find the endpoints of the ![]() interval that corresponds to one petal, we need to solve the equation
interval that corresponds to one petal, we need to solve the equation ![]() . We have
. We have ![]() and the solutions are
and the solutions are ![]() since the zeros of the sine function are of the form
since the zeros of the sine function are of the form ![]() , where
, where ![]() is integer. It follows that the petal in the first quadrant corresponds to
is integer. It follows that the petal in the first quadrant corresponds to ![]() . To find the area inside this petal, use (*) from the above theorem with
. To find the area inside this petal, use (*) from the above theorem with ![]()
![]() and
and ![]()
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill A&\ds =\frac{1}{2}\int\limits_{\alpha }^{\beta }{\left[f\left(\theta \right)\right]}^{2}d\theta \hfill \\[5mm]\ds &\ds =\frac{1}{2}\int\limits_{0}^{\pi \text{/}2}{\left[3\phantom{\rule{0.2em}{0ex}}\text{sin}\left(2\theta \right)\right]}^{2}d\theta \hfill \\[5mm]\ds &\ds =\frac{1}{2}\int\limits_{0}^{\pi \text{/}2}9\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{2}\left(2\theta \right)\phantom{\rule{0.2em}{0ex}}d\theta .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-eedeb1f308ea7e19b0af50633c84ed51_l3.png)
To evaluate this integral, use the formula ![]() with
with ![]()
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill A&\ds =\frac{1}{2}\int\limits_{0}^{\pi \text{/}2}9\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{2}\left(2\theta \right)\phantom{\rule{0.2em}{0ex}}d\theta \hfill \\[5mm]\ds &\ds =\frac{9}{2}\int\limits_{0}^{\pi \text{/}2}\frac{\left(1-\text{cos}\left(4\theta \right)\right)}{2}d\theta \hfill \\[5mm]\ds &\ds =\frac{9}{4}\int\limits_{0}^{\pi \text{/}2}\left(1-\text{cos}\left(4\theta \right)\right)d\theta \hfill \\[5mm]\ds &\ds =\frac{9}{4}{\left(\theta -\frac{\text{sin}\left(4\theta \right)}{4}\right)}\Big|_{0}^{\pi \text{/}2}\hfill \\[5mm]\ds &\ds =\frac{9}{4}\left(\frac{\pi }{2}-\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}(2\pi) }{4}\right)-\frac{9}{4}\left(0-\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}\left(0\right)}{4}\right)\hfill \\[5mm]\ds &\ds =\frac{9\pi }{8}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-3668c3000ca34bb45ea23fe081376413_l3.png)
Find the area inside the cardioid defined by the equation ![]()
Answer
![]()
Hint
Use (*). Be sure to determine the correct limits of integration before evaluating.
In the previous example, we were looking for the area inside one curve. We can also use (*) to find the area between two polar curves. For this, we need to find the points of intersection of the curves, determine which function defines the outer curve and which defines the inner curve, and then subtract the corresponding polar areas. This process is illustrated in the example below.
Finding the Area between Two Polar Curves
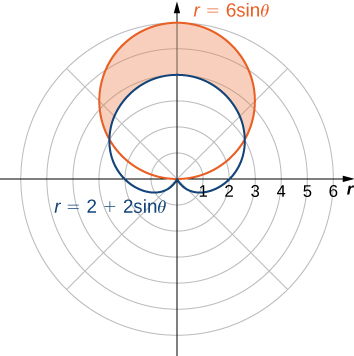
Find the area outside the cardioid ![]() and inside the circle
and inside the circle ![]()
Solution
First draw a graph containing both curves as shown below.
 and
and 
To determine the limits of integration, first find the points of intersection by setting the two functions equal to each other and solving for ![]()
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill 6\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) &\ds =\hfill &\ds 2+2\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds \hfill 4\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) &\ds =\hfill &\ds 2\hfill \\[5mm]\ds \hfill \text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) &\ds =\hfill &\ds \frac{1}{2}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-9ea7d474125020006fb2119fbba344d5_l3.png)
This gives the solutions ![]() and
and ![]() in the interval
in the interval ![]() , which are the limits of integration since from the picture we see that
, which are the limits of integration since from the picture we see that ![]() on
on ![]() . The circle
. The circle ![]() is the red graph, which is the outer function, and the cardioid
is the red graph, which is the outer function, and the cardioid ![]() is the blue graph, which is the inner function. To calculate the area between the curves, start with the area inside the circle between
is the blue graph, which is the inner function. To calculate the area between the curves, start with the area inside the circle between ![]() and
and ![]() then subtract the area inside the cardioid between
then subtract the area inside the cardioid between ![]() and
and ![]()
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill A&\ds =\text{circle}-\text{cardioid}\hfill \\[5mm]\ds &\ds =\frac{1}{2}\int\limits_{\pi \text{/}6}^{5\pi \text{/}6}{\left[6\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \right]}^{2}d\theta -\frac{1}{2}\int\limits_{\pi \text{/}6}^{5\pi \text{/}6}{\left[2+2\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \right]}^{2}d\theta \hfill \\[5mm]\ds &\ds =\frac{1}{2}\int\limits_{\pi \text{/}6}^{5\pi \text{/}6}36\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{2}(\theta) \phantom{\rule{0.2em}{0ex}}d\theta -\frac{1}{2}\int\limits_{\pi \text{/}6}^{5\pi \text{/}6}\left(4+8\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) +4\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{2}(\theta)\right)\,d\theta \hfill \\[5mm]\ds &\ds =18\int\limits_{\pi \text{/}6}^{5\pi \text{/}6}\frac{1-\text{cos}\left(2\theta \right)}{2}d\theta -2\int\limits_{\pi \text{/}6}^{5\pi \text{/}6}\left(1+2\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) +\frac{1-\text{cos}\left(2\theta \right)}{2}\right)d\theta \hfill \\[5mm]\ds &\ds =9{\left(\theta -\frac{\text{sin}\left(2\theta \right)}{2}\right)}\Big|_{\pi \text{/}6}^{5\pi \text{/}6}-2{\left(\frac{3\theta }{2}-2\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) -\frac{\text{sin}\left(2\theta \right)}{4}\right)}\Big|_{\pi \text{/}6}^{5\pi \text{/}6}\hfill \\[5mm]\ds &\ds =9\left(\frac{5\pi }{6}-\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}\left(5\pi \text{/}3\right)}{2}\right)-9\left(\frac{\pi }{6}-\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}\left(\pi \text{/}3\right)}{2}\right)\hfill \\[5mm]\ds &\ds \phantom{\rule{0.4em}{0ex}} - \left(3\left(\frac{5\pi }{6}\right)-4\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\frac{5\pi }{6}-\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}\left(5\pi \text{/}3\right)}{2}\right)+\left(3\left(\frac{\pi }{6}\right)-4\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}\frac{\pi }{6}-\frac{\text{sin}\phantom{\rule{0.2em}{0ex}}\left(\pi \text{/}3\right)}{2}\right)\hfill \\[5mm]\ds &\ds =4\pi .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-612f0f4f237e7c584155a278c391a2ba_l3.png)
Analysis
Notice that equating the formulas and solving for ![]() only yielded two solutions:
only yielded two solutions: ![]() and
and ![]() However, in the graph there are three intersection points. The third intersection point is the pole. The reason why this point did not show up as a solution is because the pole is on both graphs but corresponds to different values of
However, in the graph there are three intersection points. The third intersection point is the pole. The reason why this point did not show up as a solution is because the pole is on both graphs but corresponds to different values of ![]() Indeed, for the cardioid we get
Indeed, for the cardioid we get
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill 2+2\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) &\ds =\hfill &\ds 0\hfill \\[5mm]\ds \hfill \text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) &\ds =\hfill &\ds -1,\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-fc2deb389cf07556f6828cfebb9aefa7_l3.png)
so the values for ![]() that solve this equation are
that solve this equation are ![]() where k is an integer. For the circle we get
where k is an integer. For the circle we get
![]()
The solutions to this equation are of the form ![]() for any integer value of n. These two solution sets have no points in common. Regardless of this fact, the curves intersect at the pole. This case must always be taken into consideration, although in this partcular example it did not affect the calculations.
for any integer value of n. These two solution sets have no points in common. Regardless of this fact, the curves intersect at the pole. This case must always be taken into consideration, although in this partcular example it did not affect the calculations.
Find the area inside the circle ![]() and outside the circle
and outside the circle ![]()
Answer
![]()
Hint
Use (*) and take advantage of symmetry.
Arc Length for Polar Curves
Here we derive a formula for the arc length of a curve defined in polar coordinates.
In rectangular coordinates, the arc length of a parameterized curve ![]() for
for ![]() is given by
is given by
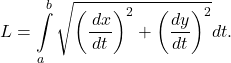
In polar coordinates we define the curve by the equation ![]() where
where ![]() In order to adapt the arc length formula for a polar curve, we use the equations
In order to adapt the arc length formula for a polar curve, we use the equations
![]()
Differentiating, we obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{c}\ds\frac{\,dx }{d\theta }={f}^{\prime }\left(\theta \right)\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) -f\left(\theta \right)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds \frac{dy}{d\theta }={f}^{\prime }\left(\theta \right)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) +f\left(\theta \right)\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7ea4af7ea45d65bb0d791d53a5b6e2ee_l3.png)
Applying the known arc length formula, we get
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill L&\ds =\int\limits_{\alpha }^{\beta }\sqrt{{\left(\frac{\,dx }{d\theta }\right)}^{2}+{\left(\frac{dy}{d\theta }\right)}^{2}}d\theta \hfill \\[5mm]\ds &\ds =\int\limits_{\alpha }^{\beta }\sqrt{{\big({f}^{\prime }\left(\theta \right)\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) -f\left(\theta \right)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \big)}^{2}+{\big({f}^{\prime }\left(\theta \right)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) +f\left(\theta \right)\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) \big)}^{2}}d\theta \hfill \\[5mm]\ds &\ds =\int\limits_{\alpha }^{\beta }\sqrt{{\left({f}^{\prime }\left(\theta \right)\right)}^{2}\left({\text{cos}}^{2}(\theta) +{\text{sin}}^{2}(\theta) \right)+{\left(f\left(\theta \right)\right)}^{2}\left({\text{cos}}^{2}(\theta) +{\text{sin}}^{2}(\theta) \right)}d\theta \hfill \\[5mm]\ds &\ds =\int\limits_{\alpha }^{\beta }\sqrt{{\left({f}^{\prime }\left(\theta \right)\right)}^{2}+{\left(f\left(\theta \right)\right)}^{2}}d\theta \hfill \\[5mm]\ds &\ds =\int\limits_{\alpha }^{\beta }\sqrt{{r}^{2}+{\left(\frac{dr}{d\theta }\right)}^{2}}d\theta .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-8a098f98692417b2856d45a3bec5c174_l3.png)
This gives us the following theorem.
Arc Length of a Curve Defined by a Polar Function
Let ![]() be a function whose derivative is continuous on an interval
be a function whose derivative is continuous on an interval ![]() The length of the polar curve
The length of the polar curve ![]() from
from ![]() to
to ![]() is
is
![Rendered by QuickLaTeX.com \ds L=\int\limits_{\alpha }^{\beta }\sqrt{{\left[f\left(\theta \right)\right]}^{2}+{\left[{f}^{\prime }\left(\theta \right)\right]}^{2}}d\theta =\int\limits_{\alpha }^{\beta }\sqrt{{r}^{2}+{\left(\frac{dr}{d\theta }\right)}^{2}}d\theta .](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7e98e49e7a85cacf6a503e8590938946_l3.png)
Finding the Arc Length of a Polar Curve
Find the arc length of the cardioid ![]()
Solution
As ![]() goes from
goes from ![]() to
to ![]() the cardioid is traced out exactly once. Therefore we can use those as the limits of integration in the formula from the above theorem to obtain
the cardioid is traced out exactly once. Therefore we can use those as the limits of integration in the formula from the above theorem to obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill L&\ds =\int\limits_{-\pi}^{\pi }\sqrt{{\left[2+2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) \right]}^{2}+{\left[-2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \right]}^{2}}\phantom{\rule{0.2em}{0ex}}d\theta \hfill \\[5mm]\ds &\ds =\int\limits_{-\pi}^{\pi }\sqrt{4+8\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) +4\phantom{\rule{0.1em}{0ex}}{\text{cos}}^{2}\phantom{\rule{0.1em}{0ex}}(\theta) +4\phantom{\rule{0.1em}{0ex}}{\text{sin}}^{2}\phantom{\rule{0.1em}{0ex}}(\theta) }\phantom{\rule{0.2em}{0ex}}d\theta \hfill \\[5mm]\ds &\ds =\int\limits_{-\pi}^{\pi }\sqrt{4+8\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) +4\left({\text{cos}}^{2}\phantom{\rule{0.1em}{0ex}}(\theta) +{\text{sin}}^{2}\phantom{\rule{0.1em}{0ex}}(\theta) \right)}\phantom{\rule{0.2em}{0ex}}d\theta \hfill \\[5mm]\ds &\ds =\int\limits_{-\pi}^{\pi }\sqrt{8+8\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) }\phantom{\rule{0.2em}{0ex}}d\theta \hfill \\[5mm]\ds &\ds =2\int\limits_{-\pi}^{\pi }\sqrt{2+2\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) }\phantom{\rule{0.2em}{0ex}}d\theta .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-717b335ebae39c78316dc927ff064810_l3.png)
Next, the identity ![]() implies that
implies that![]() Substituting
Substituting ![]() gives
gives ![]() so the integral becomes
so the integral becomes
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill L&\ds =2\int\limits_{-\pi}^{\pi }\sqrt{2+2\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) }d\theta \hfill \\[5mm]\ds &\ds =2\int\limits_{-\pi}^{\pi }\sqrt{4\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{2}\left(\frac{\theta }{2}\right)}d\theta \hfill \\[5mm]\ds &\ds =2\int\limits_{-\pi}^{\pi }2\left|\text{cos}\left(\frac{\theta }{2}\right)\right|d\theta .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-ff96ea09eb28f4a8bf143a23f991f557_l3.png)
When ![]() , we have that
, we have that ![]() and since cosine is non-negative on this interval, the absolute value can be dropped and we obtain
and since cosine is non-negative on this interval, the absolute value can be dropped and we obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill L&\ds =4\int\limits_{-\pi}^{\pi }\text{cos}\left(\frac{\theta }{2}\right)\,d\theta \hfill \\[5mm]\ds &\ds =4{\left(2\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\frac{\theta }{2}\right)\right)}\Big|_{-\pi}^{\pi }\hfill \\[5mm]\ds &\ds =8(1-(-1))=16.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-a02d4e6d3e09206fa8bf32c5452cbe11_l3.png)
Find the total arc length of ![]()
Answer
![]()
Hint
To determine the correct limits, make a table of values.
Key Concepts
- The area of the region bounded by the polar curve
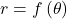 and between the radial lines
and between the radial lines 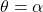 and
and 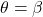 is given by the integral
is given by the integral ![Rendered by QuickLaTeX.com \ds A=\frac{1}{2}{\int\limits_{\alpha }^{\beta }\left[f\left(\theta \right)\right]}^{2}d\theta .](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-52fbbd7d3484641bf5edbafb6da69158_l3.png)
- To find the area between two curves in the polar coordinate system, first find the points of intersection, then subtract the corresponding areas.
- The arc length of a polar curve defined by the equation
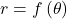 with
with 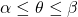 is given by the integral
is given by the integral ![Rendered by QuickLaTeX.com \ds L=\int\limits_{\alpha }^{\beta }\sqrt{{\left[f\left(\theta \right)\right]}^{2}+{\left[{f}^{\prime }\left(\theta \right)\right]}^{2}}d\theta =\int\limits_{\alpha }^{\beta }\sqrt{{r}^{2}+{\left(\frac{dr}{d\theta }\right)}^{2}}d\theta .](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7e98e49e7a85cacf6a503e8590938946_l3.png)
Key Equations
- Area of a region bounded by a polar curve
![Rendered by QuickLaTeX.com \ds A=\frac{1}{2}\int\limits_{\alpha }^{\beta }{\left[f\left(\theta \right)\right]}^{2}d\theta =\frac{1}{2}\int\limits_{\alpha }^{\beta }{r}^{2}d\theta](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-584a40241c984a3b9796029bcd6657e6_l3.png)
- Arc length of a polar curve
![Rendered by QuickLaTeX.com \ds L=\int\limits_{\alpha }^{\beta }\sqrt{{\left[f\left(\theta \right)\right]}^{2}+{\left[{f}^{\prime }\left(\theta \right)\right]}^{2}}d\theta =\int\limits_{\alpha }^{\beta }\sqrt{{r}^{2}+{\left(\frac{dr}{d\theta }\right)}^{2}}d\theta](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-e3e6f5cf0ec31b042643294011a84648_l3.png)
Exercises
For the following exercises, determine a definite integral that represents the area of the given region.
1. Region enclosed by ![]()
Answer
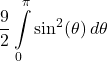
2. Region in the first quadrant within the cardioid ![]()
3. Region enclosed by one petal of ![]() .
.
Answer
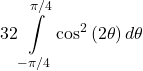
4. Region enclosed by one petal of ![]() .
.
5. Region below the polar axis and enclosed by ![]()
Answer
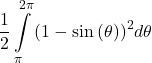
6. Region in the first quadrant enclosed by ![]()
7. Region enclosed by the inner loop of ![]()
(Hint: inner loop corresponds to ![]() .)
.)
Answer
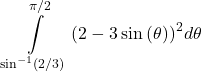
8. Region enclosed by the inner loop of ![]()
9. Region enclosed by ![]() and outside the inner loop.
and outside the inner loop.
Answer
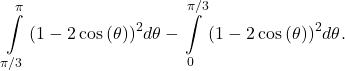
10. Region common to ![]()
(Hint: divide the region into several parts so that each of the parts is determined by one of the curves.)
11. Region common to ![]()
(Hint: divide the region into several parts so that each of the parts is determined by one of the curves.)
Answer
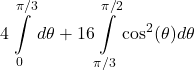
12. Region common to ![]()
(Hint: divide the region into several parts so that each of the parts is determined by one of the curves.)
For the following exercises, find the area of the described region.
13. Region enclosed by ![]()
Answer
![]()
14. Region above the polar axis and enclosed by ![]()
15. Region below the polar axis and enclosed by ![]()
Answer
![]()
16. Region enclosed by one petal of ![]()
17. Region enclosed by one petal of ![]()
Answer
![]()
18. Region enclosed by ![]()
19. Region enclosed by the inner loop of ![]()
Answer
![]()
20. Region enclosed by ![]() and outside the inner loop.
and outside the inner loop.
21. Common interior of ![]()
Answer
![]()
22. Common interior of ![]()
23. Common interior of ![]()
Answer
![]()
For the following exercises, find a definite integral that represents the arc length.
24. ![]()
25. ![]() ,
, ![]()
Answer
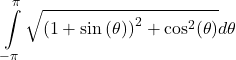
26. ![]()
27. ![]()
Answer
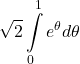
For the following exercises, find the length of the curve over the given interval.
28. ![]()
29. ![]()
Answer
![]()
30. ![]()
31. ![]()
Answer
32
32. ![]()
![]()
For the following exercises, use the integration capabilities of a calculator to approximate the length of the curve.
33. [T]![]()
Answer
6.238
34. [T]![]()
35. [T]![]()
Answer
2
36. [T]![]()
37. [T]![]()
Answer
4.39
For the following exercises, rewrite the equation of the given polar curve in rectangular coordinates and use the familiar formula from geometry to find the area enclosed by the curve. Confirm your answer by using the definite integral.
38. ![]()
39. ![]()
Answer
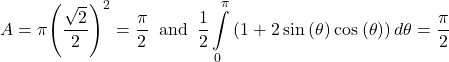
For the following exercises, use the familiar formula from geometry to find the length of the curve and then confirm using the definite integral.
40. ![]()
Answer
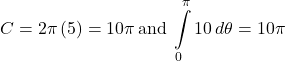
41. ![]()
42. Show that the curve ![]() (called a cissoid of Diocles) has the line
(called a cissoid of Diocles) has the line ![]() as a vertical asymptote.
as a vertical asymptote.
(Hint: the line ![]() has polar equation
has polar equation ![]() .)
.)

