"

Review of Pre-Calculus

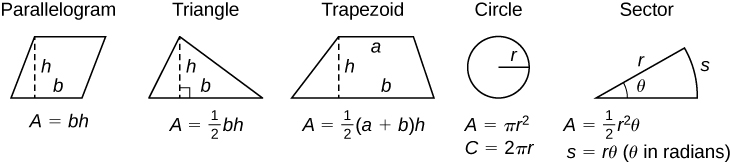
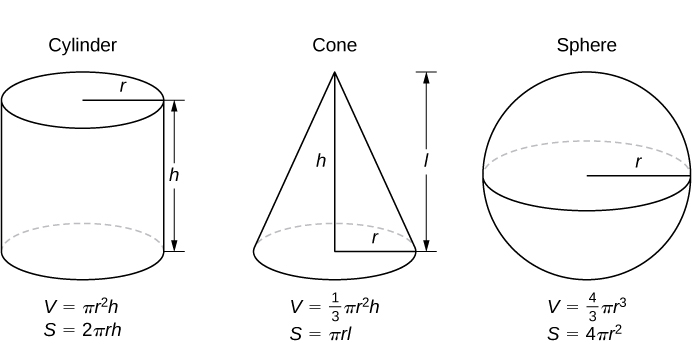
Formulas from Geometry

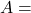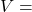A=Area, V=Volume, and 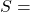S=Lateral Surface Area

The figure shows five geometric figures. The first is a parallelogram with height labeled as h and base as b. Below the figure is the formula for area, A = bh. The second is a triangle with height labeled as h and base as b. Below the figure is the formula for area, A = (1/2)bh.. The third is a trapezoid with the top horizontal side labeled as a, height as h, and base as b. Below the figure is the formula for area, A = (1/2)(a + b)h. The fourth is a circle with radius labeled as r. Below the figure is the formula for area, A= (pi)(r^2), and the formula for circumference, C = 2(pi)r. The fifth is a sector of a circle with radius labeled as r, sector length as s, and angle as theta. Below the figure is the formula for area, A = (1/2)r^2(theta), and sector length, s = r(theta) (theta in radians).The figure shows three solid figures. The first is a cylinder with height labeled as h and radius as r. Below the figure are the formulas for volume, V = (pi)(r^2)h, and surface area, S = 2(pi)rh. The second is a cone with height labeled as h, radius as r, and lateral side length as l. Below the figure are the formulas for volume, V = (1/3)(pi)(r^2)h, and surface area, S = (pi)rl. The third is a sphere with radius labeled as r. Below the figure are the formulas for volume, V = (4/3)(pi)(r^3), and surface area, S = 4(pi)r^2.

Formulas from Algebra

Laws of Exponents

\begin{array}{ccccccccccccc}\hfill {x}^{m}{x}^{n}& =\hfill & {x}^{m+n}\hfill & & & \hfill \dfrac{{x}^{m}}{{x}^{n}}& =\hfill & {x}^{m-n}\hfill & & & \hfill {\left({x}^{m}\right)}^{n}& =\hfill & {x}^{mn}\hfill \\[3mm] \hfill {x}^{-n}& =\hfill & \dfrac{1}{{x}^{n}}\hfill & & & \hfill {\left(xy\right)}^{n}& =\hfill & {x}^{n}{y}^{n}\hfill & & & \hfill {\left(\dfrac{x}{y}\right)}^{n}& =\hfill & \dfrac{{x}^{n}}{{y}^{n}}\hfill \\[3mm] \hfill {x}^{1\text{/}n}& =\hfill & \sqrt[n]{x}\hfill & & & \hfill \sqrt[n]{xy}& =\hfill & \sqrt[n]{x}\sqrt[n]{y}\hfill & & & \hfill \sqrt[n]{\dfrac{x}{y}}& =\hfill & \dfrac{\sqrt[n]{x}}{\sqrt[n]{y}}\hfill \\[3mm] \hfill {x}^{m\text{/}n}& =\hfill & \sqrt[n]{{x}^{m}}={\left(\sqrt[n]{x}\right)}^{m}\hfill & & & & & & & & & & \end{array}

Special Factorizations

\begin{array}{ccc}\hfill {x}^{2}-{y}^{2}& =\hfill & \left(x+y\right)\left(x-y\right)\hfill \\[1mm] \hfill {x}^{3}+{y}^{3}& =\hfill & \left(x+y\right)\left({x}^{2}-xy+{y}^{2}\right)\hfill \\[1mm] \hfill {x}^{3}-{y}^{3}& =\hfill & \left(x-y\right)\left({x}^{2}+xy+{y}^{2}\right)\hfill \end{array}

Quadratic Formula

If a{x}^{2}+bx+c=0, then x=\dfrac{-b\pm\sqrt{{b}^{2}-4ca}}{2a}.

Binomial Theorem

{\left(a+b\right)}^{n}={a}^{n}+\left(\begin{array}{l}n\\ 1\end{array}\right){a}^{n-1}b+\left(\begin{array}{l}n\\ 2\end{array}\right){a}^{n-2}{b}^{2}+\cdots +\left(\begin{array}{c}n\\ n-1\end{array}\right)a{b}^{n-1}+{b}^{n},

where \left(\begin{array}{l}n\\ k\end{array}\right)=\dfrac{n\left(n-1\right)\left(n-2\right)\cdots \left(n-k+1\right)}{k\left(k-1\right)\left(k-2\right)\cdots 3\cdot 2\cdot 1}=\dfrac{n!}{k!\left(n-k\right)!}

Formulas from Trigonometry

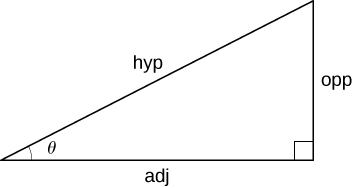
Right-Angle Trigonometry

\begin{array}{cccc}\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) =\dfrac{\text{opp}}{\text{hyp}}\hfill & & & \text{csc}\phantom{\rule{0.1em}{0ex}}(\theta) =\dfrac{\text{hyp}}{\text{opp}}\hfill \\[3mm] \text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) =\dfrac{\text{adj}}{\text{hyp}}\hfill & & & \text{sec}\phantom{\rule{0.1em}{0ex}}(\theta) =\dfrac{\text{hyp}}{\text{adj}}\hfill \\[3mm] \text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) =\dfrac{\text{opp}}{\text{adj}}\hfill & & & \text{cot}\phantom{\rule{0.1em}{0ex}}(\theta) =\dfrac{\text{adj}}{\text{opp}}\hfill \end{array}

The figure shows a right triangle with the longest side labeled hyp, the shorter leg labeled as opp, and the longer leg labeled as adj. The angle between the hypotenuse and the adjacent side is labeled theta.

Trigonometric Functions of Important Angles

\theta \text{Radians} \text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) \text{tan}\phantom{\rule{0.1em}{0ex}}(\theta)
0\text{°} 0 0 1 0
30\text{°} {\pi}\text{/}\text{6} 1\text{/}2 \sqrt{3}\text{/}2 \sqrt{3}\text{/}3
45\text{°} {\pi}\text{/}\text{4} \sqrt{2}\text{/}2 \sqrt{2}\text{/}2 1
60\text{°} {\pi}\text{/}\text{3} \sqrt{3}\text{/}2 1\text{/}2 \sqrt{3}
90\text{°} {\pi}\text{/}2 1 0 —

Fundamental Identities

\begin{array}{cccccccc}\hfill {\text{sin}}^{2}(\theta) +{\text{cos}}^{2}(\theta) & =\hfill & 1\hfill & & & \hfill \text{sin}\left(-\phantom{\rule{0.1em}{0ex}}\theta \right)& =\hfill & -\text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \hfill \\[1mm] \hfill 1+{\text{tan}}^{2}(\theta) & =\hfill & {\text{sec}}^{2}(\theta) \hfill & & & \hfill \text{cos}\left(-\phantom{\rule{0.1em}{0ex}}\theta \right)& =\hfill & \text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) \hfill \\[1mm] \hfill 1+{\text{cot}}^{2}(\theta) & =\hfill & {\text{csc}}^{2}(\theta) \hfill & & & \hfill \text{tan}\left(-\phantom{\rule{0.1em}{0ex}}\theta \right)& =\hfill & -\text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) \hfill \\[2mm] \hfill \text{sin}\left(\frac{\pi }{2}-\theta \right)& =\hfill & \text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) \hfill & & & \hfill \text{sin}\left(\theta +2\pi \right)& =\hfill & \text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \hfill \\[2mm] \hfill \text{cos}\left(\frac{\pi }{2}-\theta \right)& =\hfill & \text{sin}\phantom{\rule{0.1em}{0ex}}(\theta) \hfill & & & \hfill \text{cos}\left(\theta +2\pi \right)& =\hfill & \text{cos}\phantom{\rule{0.1em}{0ex}}(\theta) \hfill \\[2mm] \hfill \text{tan}\left(\frac{\pi }{2}-\theta \right)& =\hfill & \text{cot}\phantom{\rule{0.1em}{0ex}}(\theta) \hfill & & & \hfill \text{tan}\left(\theta +\pi \right)& =\hfill & \text{tan}\phantom{\rule{0.1em}{0ex}}(\theta) \hfill \end{array}

Law of Sines

\dfrac{\text{sin}\phantom{\rule{0.1em}{0ex}}(A)}{a}=\dfrac{\text{sin}\phantom{\rule{0.1em}{0ex}}(B)}{b}=\dfrac{\text{sin}\phantom{\rule{0.1em}{0ex}}(C)}{c}

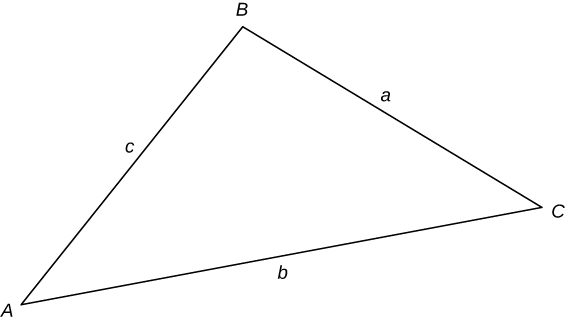
The figure shows a nonright triangle with vertices labeled A, B, and C. The side opposite angle A is labeled a. The side opposite angle B is labeled b. The side opposite angle C is labeled c.

Law of Cosines

\begin{array}{ccc}\hfill {a}^{2}& =\hfill & {b}^{2}+{c}^{2}-2bc\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(A)\hfill \\[1mm] \hfill {b}^{2}& =\hfill & {a}^{2}+{c}^{2}-2ac\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(B)\hfill \\[1mm] \hfill {c}^{2}& =\hfill & {a}^{2}+{b}^{2}-2ab\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(C)\hfill \end{array}

Addition and Subtraction Formulas

\begin{array}{ccc}\hfill \text{sin}\phantom{\rule{0.2em}{0ex}}\left(x+y\right)& =\hfill & \text{sin}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(y)+\text{cos}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(y)\hfill \\[1mm] \hfill \text{sin}\phantom{\rule{0.1em}{0ex}}\left(x-y\right)& =\hfill & \text{sin}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(y)-\text{cos}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(y)\hfill \\[1mm] \hfill \text{cos}\phantom{\rule{0.1em}{0ex}}\left(x+y\right)& =\hfill & \text{cos}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(y)-\text{sin}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(y)\hfill \\[1mm] \hfill \text{cos}\phantom{\rule{0.1em}{0ex}}\left(x-y\right)& =\hfill & \text{cos}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(y)+\text{sin}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(y)\hfill \\[2mm] \hfill \text{tan}\phantom{\rule{0.1em}{0ex}}\left(x+y\right)& =\hfill & \dfrac{\text{tan}\phantom{\rule{0.2em}{0ex}}(x)+\text{tan}(y)}{1-\text{tan}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{tan}(y)}\hfill \\[3mm] \hfill \text{tan}\left(x-y\right)& =\hfill & \dfrac{\text{tan}\phantom{\rule{0.2em}{0ex}}(x)-\text{tan}(y)}{1+\text{tan}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{tan}(y)}\hfill \end{array}

Double-Angle Formulas

\begin{array}{ccc}\hfill \text{sin}\phantom{\rule{0.2em}{0ex}}(2x)& =\hfill & 2\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(x)\hfill \\[1mm] \hfill \text{cos}\phantom{\rule{0.2em}{0ex}}(2x)& =\hfill & {\text{cos}}^{2}(x)-{\text{sin}}^{2}(x)=2\phantom{\rule{0.1em}{0ex}}{\text{cos}}^{2}(x)-1=1-2\phantom{\rule{0.1em}{0ex}}{\text{sin}}^{2}(x)\hfill \\[2mm] \hfill \text{tan}\phantom{\rule{0.2em}{0ex}}(2x)& =\hfill & \dfrac{2\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.2em}{0ex}}(x)}{1-{\text{tan}}^{2}(x)}\hfill \end{array}

Half-Angle Formulas

\begin{array}{ccc}\hfill {\text{sin}}^{2}(x)& =\hfill & \dfrac{1-\text{cos}\phantom{\rule{0.2em}{0ex}}(2x)}{2}\hfill \\[3mm] \hfill {\text{cos}}^{2}(x)& =\hfill & \dfrac{1+\text{cos}\phantom{\rule{0.2em}{0ex}}(2x)}{2}\hfill \end{array}

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Calculus: Volume 2 (Second University of Manitoba Edition) Copyright © 2021 by Gilbert Strang and Edward 'Jed' Herman, modified by Varvara Shepelska is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book