7.3 Polar Coordinates
Learning Objectives
- Locate points in a plane using polar coordinates.
- Convert points between rectangular and polar coordinates.
- Sketch polar curves with given equations.
- Convert equations between rectangular and polar coordinates.
- Identify symmetry in polar curves and equations.
The rectangular coordinate system (or Cartesian plane) provides a means of mapping points to ordered pairs and ordered pairs to points. This is called a one-to-one mapping from points in the plane to ordered pairs. The polar coordinate system provides an alternative method of mapping points to ordered pairs. In this section we see that in some circumstances, polar coordinates can be more useful than rectangular coordinates.
Defining Polar Coordinates
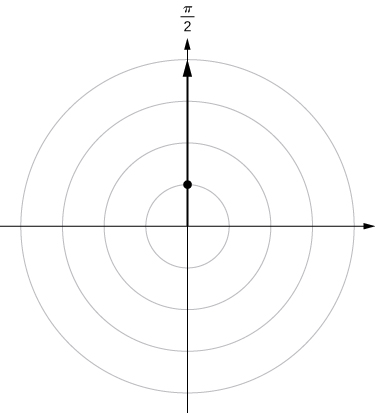
To find the coordinates of a point in the polar coordinate system, consider Figure 1 below. The point ![]() has Cartesian coordinates
has Cartesian coordinates ![]() Consider the line segment connecting the origin to the point
Consider the line segment connecting the origin to the point ![]() . Its length is equal to the distance from the origin to
. Its length is equal to the distance from the origin to ![]() and we denote it by
and we denote it by ![]() We also denote the angle between the positive
We also denote the angle between the positive ![]() -axis and the line segment by
-axis and the line segment by ![]() Then
Then ![]() are the polar coordinates of
are the polar coordinates of ![]()
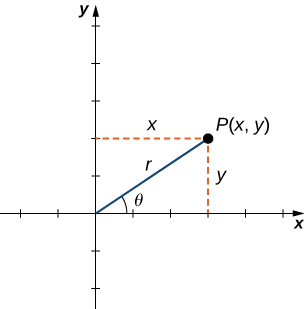
Each point ![]() in the Cartesian coordinate system can be represented as an ordered pair
in the Cartesian coordinate system can be represented as an ordered pair ![]() in the polar coordinate system. The first coordinate is called the radial coordinate and the second coordinate is called the angular coordinate. In the polar coordinate system, the origin is called the pole and the positive x-axis is the polar axis. Note that every point in the Cartesian plane has two values (hence the term ordered pair) associated with it. In the polar coordinate system, each point also has two values associated with it:
in the polar coordinate system. The first coordinate is called the radial coordinate and the second coordinate is called the angular coordinate. In the polar coordinate system, the origin is called the pole and the positive x-axis is the polar axis. Note that every point in the Cartesian plane has two values (hence the term ordered pair) associated with it. In the polar coordinate system, each point also has two values associated with it: ![]() and
and ![]()
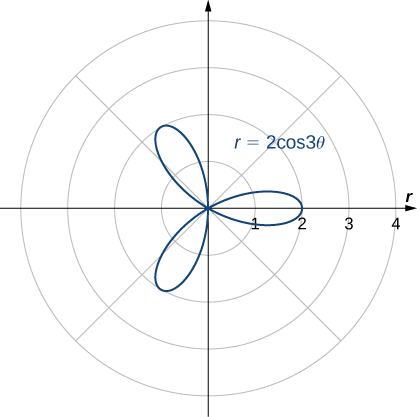
Using right-triangle trigonometry, we obtain the following equations:
![]()
![]()
Furthermore,
![]()
These formulas can be used to convert from rectangular to polar or from polar to rectangular coordinates.
Note that the equation ![]() has an infinite number of solutions for any ordered pair
has an infinite number of solutions for any ordered pair ![]() However, if we restrict the solutions
However, if we restrict the solutions ![]() to values in
to values in ![]() , then we can assign a unique solution to the quadrant in which the point
, then we can assign a unique solution to the quadrant in which the point ![]() is located.
is located.
Converting Points between Coordinate Systems
Given a point ![]() in the plane with Cartesian coordinates
in the plane with Cartesian coordinates ![]() and polar coordinates
and polar coordinates ![]() the following conversion formulas hold true:
the following conversion formulas hold true:
![]()
![]()
Converting between Rectangular and Polar Coordinates
Convert the following rectangular coordinates into polar coordinates.
Convert the following polar coordinates into rectangular coordinates.
Solution
- Use
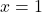 and
and 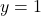 in (**):
in (**):
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccccc}\begin{array}{ccc}\hfill {r}^{2}&\ds =\hfill &\ds {x}^{2}+{y}^{2}\hfill \\[5mm]\ds &\ds =\hfill &\ds {1}^{2}+{1}^{2}\hfill \\[5mm]\ds \hfill r&\ds =\hfill &\ds \sqrt{2}\hfill \end{array}\hfill &\ds &\ds &\ds \text{and}\hfill &\ds &\ds &\ds \begin{array}{ccc}\hfill \text{tan}\phantom{\rule{0.2em}{0ex}}(\theta) &\ds =\hfill &\ds \frac{y}{x}\hfill \\[5mm]\ds &\ds =\hfill &\ds \frac{1}{1}=1\hfill \\[5mm]\ds \hfill \theta &\ds =\hfill &\ds \frac{\pi }{4},\hfill \end{array}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-84451dba2f2574fa720a71e0dbe8ee2a_l3.png)
where we chose the angle of
 since the point
since the point 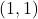 belongs to the first quadrant and hence
belongs to the first quadrant and hence ![Rendered by QuickLaTeX.com \ds\theta\in\left[0,\frac{\pi}2\right]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-26c81599038bd3c94c72df79e04a4bab_l3.png) .
.
Therefore this point can be represented as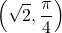 in polar coordinates.
in polar coordinates. - Use
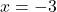 and
and 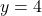 in (**):
in (**):
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccccc}\begin{array}{ccc}\hfill {r}^{2}&\ds =\hfill &\ds {x}^{2}+{y}^{2}\hfill \\[5mm]\ds &\ds =\hfill &\ds {\left(-3\right)}^{2}+{\left(4\right)}^{2}\hfill \\[5mm]\ds \hfill r&\ds =\hfill &\ds 5\hfill \end{array}\hfill &\ds &\ds &\ds \text{and}\hfill &\ds &\ds &\ds \begin{array}{ccc}\hfill \text{tan}\phantom{\rule{0.2em}{0ex}}(\theta) &\ds =\hfill &\ds \frac{y}{x}\hfill \\[5mm]\ds &\ds =\hfill &\ds -\frac{4}{3}\hfill \\[5mm]\ds \hfill \theta &\ds =\hfill &\ds \pi+ \text{arctan}\left(-\frac{4}{3}\right)\hfill \\[5mm]\ds &\ds = \hfill &\ds\pi-\arctan\left(\frac43\right),\hfill \end{array}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-f0ac05083c849e5f9fbf2543582b4c58_l3.png)
since
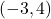 belongs to the second quadrant and hence
belongs to the second quadrant and hence ![Rendered by QuickLaTeX.com \ds\theta\in\left[\frac{\pi}2,\pi\right]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-01e88580238dc26e92518127c43c37d5_l3.png) . So the polar coordinates of this point are
. So the polar coordinates of this point are 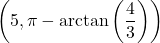 .
. - Use
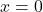 and
and 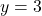 in (**):
in (**):
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccccc}\begin{array}{ccc}\hfill {r}^{2}&\ds =\hfill &\ds {x}^{2}+{y}^{2}\hfill \\[5mm]\ds &\ds =\hfill &\ds {\left(3\right)}^{2}+{\left(0\right)}^{2}\hfill \\[5mm]\ds &\ds =\hfill &\ds 9+0\hfill \\[5mm]\ds \hfill r&\ds =\hfill &\ds 3\hfill \end{array}\hfill &\ds &\ds &\ds \text{and}\hfill &\ds &\ds &\ds \begin{array}{ccc}\hfill \text{tan}\phantom{\rule{0.2em}{0ex}}(\theta) &\ds =\hfill &\ds \frac{y}{x}\hfill \\[5mm]\ds &\ds =\hfill &\ds \frac{3}{0}.\hfill \end{array}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-cc7622e44b6e5d1582c091a20ef901d2_l3.png)
Direct application of the second equation leads to division by zero. Graphing the point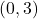 on the rectangular coordinate system reveals that the point is located on the positive y-axis. The angle between the positive x-axis and the positive y-axis is
on the rectangular coordinate system reveals that the point is located on the positive y-axis. The angle between the positive x-axis and the positive y-axis is 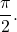 Therefore this point can be represented as
Therefore this point can be represented as 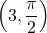 in polar coordinates.
in polar coordinates. - Use
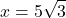 and
and 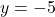 in (**):
in (**):
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccccc}\begin{array}{ccc}\hfill {r}^{2}&\ds =\hfill &\ds {x}^{2}+{y}^{2}\hfill \\[5mm]\ds &\ds =\hfill &\ds {\left(5\sqrt{3}\right)}^{2}+{\left(-5\right)}^{2}\hfill \\[5mm]\ds &\ds =\hfill &\ds 75+25\hfill \\[5mm]\ds \hfill r&\ds =\hfill &\ds 10\hfill \end{array}\hfill &\ds &\ds &\ds \text{and}\hfill &\ds &\ds &\ds \begin{array}{ccc}\hfill \text{tan}\phantom{\rule{0.2em}{0ex}}(\theta) &\ds =\hfill &\ds \frac{y}{x}\hfill \\[5mm]\ds &\ds =\hfill &\ds \frac{-5}{5\sqrt{3}}=-\frac{\sqrt{3}}{3}\hfill \\[5mm]\ds \hfill \theta &\ds =\hfill &\ds -\frac{\pi }{6},\hfill \end{array}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-c89f6a3434288d727ee99d209c519524_l3.png)
since the point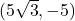 is in the fourth quadrant and hence
is in the fourth quadrant and hence ![Rendered by QuickLaTeX.com \ds\theta\in\left[-\frac{\pi}2,0\right]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-578bf65b4a695e5a56f1fe007cb7c5a9_l3.png) .
.
Therefore this point can be represented as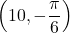 in polar coordinates.
in polar coordinates. - Use
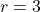 and
and 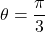 in (*)
in (*)
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccccc}\begin{array}{ccc}\hfill x&\ds =\hfill &\ds r\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds &\ds =\hfill &\ds 3\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\frac{\pi }{3}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds 3\left(\frac{1}{2}\right)=\frac{3}{2}\hfill \end{array}\hfill &\ds &\ds &\ds \text{and}\hfill &\ds &\ds &\ds \begin{array}{ccc}\hfill y&\ds =\hfill &\ds r\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds &\ds =\hfill &\ds 3\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\frac{\pi }{3}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds 3\left(\frac{\sqrt{3}}{2}\right)=\frac{3\sqrt{3}}{2}.\hfill \end{array}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-e08ed5a81ae546369613041798b1c39e_l3.png)
Therefore this point can be represented as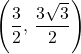 in rectangular coordinates.
in rectangular coordinates. - Use
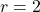 and
and 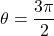 in (*):
in (*):
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccccc}\begin{array}{ccc}\hfill x&\ds =\hfill &\ds r\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds &\ds =\hfill &\ds 2\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\frac{3\pi }{2}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds 2\left(0\right)=0\hfill \end{array}\hfill &\ds &\ds &\ds \text{and}\hfill &\ds &\ds &\ds \begin{array}{ccc}\hfill y&\ds =\hfill &\ds r\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds &\ds =\hfill &\ds 2\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\frac{3\pi }{2}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds 2\left(-1\right)=-2.\hfill \end{array}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-8917d85b77a5d53cc61fe2d6bb92e904_l3.png)
Therefore this point can be represented as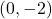 in rectangular coordinates.
in rectangular coordinates. - Use
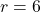 and
and 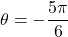 in (*):
in (*):
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccccc}\begin{array}{ccc}\hfill x&\ds =\hfill &\ds r\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds &\ds =\hfill &\ds 6\phantom{\rule{0.2em}{0ex}}\text{cos}\left(-\frac{5\pi }{6}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds 6\left(-\frac{\sqrt{3}}{2}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds -3\sqrt{3}\hfill \end{array}\hfill &\ds &\ds &\ds \text{and}\hfill &\ds &\ds &\ds \begin{array}{ccc}\hfill y&\ds =\hfill &\ds r\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds &\ds =\hfill &\ds 6\phantom{\rule{0.2em}{0ex}}\text{sin}\left(-\frac{5\pi }{6}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds 6\left(-\frac{1}{2}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds -3.\hfill \end{array}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-044432e712762f84b3f72f7792864203_l3.png)
Therefore this point can be represented as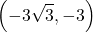 in rectangular coordinates.
in rectangular coordinates.
Convert ![]() from rectangular into polar coordinates and
from rectangular into polar coordinates and ![]() — from polar coordinates into rectangular coordinates.
— from polar coordinates into rectangular coordinates.
Answer
![]() and
and ![]()
Hint
Make sure to check the quadrant when calculating ![]()
The polar representation of a point is not unique. For example, the polar coordinates ![]() and
and ![]() both represent the point
both represent the point ![]() in the rectangular system. We can also allow
in the rectangular system. We can also allow ![]() to be negative. For example, the point with polar coordinates
to be negative. For example, the point with polar coordinates ![]() also represents the point
also represents the point ![]() in the rectangular system, as we can see by using (*):
in the rectangular system, as we can see by using (*):
![Rendered by QuickLaTeX.com \ds \begin{array}{ccccccc}\begin{array}{ccc}\hfill x&\ds =\hfill &\ds r\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds &\ds =\hfill &\ds -2\phantom{\rule{0.2em}{0ex}}\text{cos}\left(\frac{4\pi }{3}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds -2\left(-\frac{1}{2}\right)=1\hfill \end{array}\hfill &\ds &\ds &\ds \text{and}\hfill &\ds &\ds &\ds \begin{array}{ccc}\hfill y&\ds =\hfill &\ds r\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \hfill \\[5mm]\ds &\ds =\hfill &\ds -2\phantom{\rule{0.2em}{0ex}}\text{sin}\left(\frac{4\pi }{3}\right)\hfill \\[5mm]\ds &\ds =\hfill &\ds -2\left(-\frac{\sqrt{3}}{2}\right)=\sqrt{3}.\hfill \end{array}\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-41d1eb07a6bad2f6c31c132df4fa1490_l3.png)
(Geometrically, when we plot a point with a negative radial coordinate, we measure the distance of ![]() along the halfline that is in the opposite direction to the one that makes the angle of
along the halfline that is in the opposite direction to the one that makes the angle of ![]() with the positive x-axis, so basically the minus reverses the direction, the same way as with angles.)
with the positive x-axis, so basically the minus reverses the direction, the same way as with angles.)
Every point in the plane has an infinite number of representations in polar coordinates. However, each point in the plane has only one representation in the rectangular coordinate system.
Note that the polar representation of a point in the plane also has a visual interpretation. In particular, ![]() is the directed distance that the point lies from the origin, and
is the directed distance that the point lies from the origin, and ![]() measures the angle that the line segment from the origin to the point makes with the positive
measures the angle that the line segment from the origin to the point makes with the positive ![]() -axis. Positive angles are measured in a counterclockwise direction and negative angles are measured in a clockwise direction. The polar coordinate system appears in the following figure.
-axis. Positive angles are measured in a counterclockwise direction and negative angles are measured in a clockwise direction. The polar coordinate system appears in the following figure.
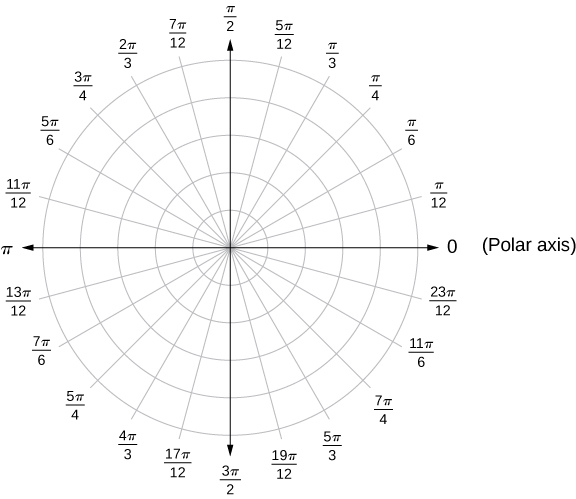
The line segment starting from the center of the graph going to the right (called the positive x-axis in the Cartesian system) is the polar axis. The center point is the pole, or origin, of the coordinate system, and corresponds to ![]() The innermost circle shown in Figure 2 above contains all points a distance of 1 unit from the pole, and is represented by the equation
The innermost circle shown in Figure 2 above contains all points a distance of 1 unit from the pole, and is represented by the equation ![]() Then
Then ![]() is the set of points 2 units from the pole, and so on. The line segments emanating from the pole correspond to fixed angles. To plot a point in the polar coordinate system, start with the angle. If the angle is positive, then measure the angle from the polar axis in a counterclockwise direction. If it is negative, then measure it clockwise. If the value of
is the set of points 2 units from the pole, and so on. The line segments emanating from the pole correspond to fixed angles. To plot a point in the polar coordinate system, start with the angle. If the angle is positive, then measure the angle from the polar axis in a counterclockwise direction. If it is negative, then measure it clockwise. If the value of ![]() is positive, move that distance along the terminal ray of the angle. If it is negative, move along the ray that is opposite to the terminal ray of the given angle.
is positive, move that distance along the terminal ray of the angle. If it is negative, move along the ray that is opposite to the terminal ray of the given angle.
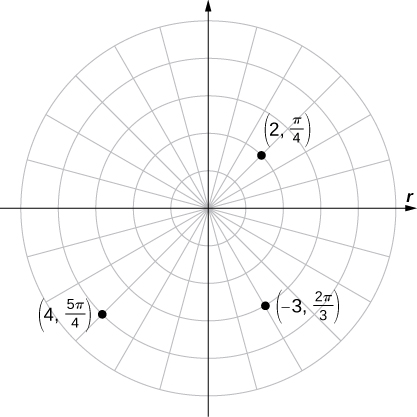
Plotting Points in the Polar Plane
Plot each of the following points on the polar plane.
Solution
The three points are plotted in the following figure.
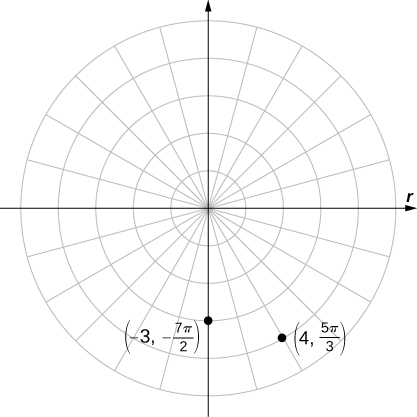
Plot ![]() and
and ![]() on the polar plane.
on the polar plane.
Answer
Polar Curves
Now that we know how to plot points in the polar coordinate system, we can discuss how to plot curves. In the rectangular coordinate system, we can graph a function ![]() and create a curve in the Cartesian plane. In a similar fashion, we can graph a curve that is generated by a function
and create a curve in the Cartesian plane. In a similar fashion, we can graph a curve that is generated by a function ![]()
The general idea behind graphing a function in polar coordinates is the same as graphing a function in rectangular coordinates. Start with a list of values for the independent variable ![]() in this case) and calculate the corresponding values of the dependent variable
in this case) and calculate the corresponding values of the dependent variable ![]() This process generates a list of ordered pairs, which can be plotted in the polar coordinate system. Finally, connect the points, and take advantage of any patterns that may appear. The function may be periodic, for example, which indicates that only a limited number of values for the independent variable are needed.
This process generates a list of ordered pairs, which can be plotted in the polar coordinate system. Finally, connect the points, and take advantage of any patterns that may appear. The function may be periodic, for example, which indicates that only a limited number of values for the independent variable are needed.
Problem-Solving Strategy: Plotting a Curve in Polar Coordinates
- Create a table with two columns. The first column is for
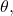 and the second column is for
and the second column is for 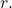
- Create a list of values for
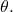
- Calculate the corresponding
 values for each
values for each 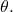
- Plot each ordered pair
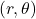 on the coordinate axes.
on the coordinate axes. - Connect the points and look for a pattern.
Graphing a Function in Polar Coordinates
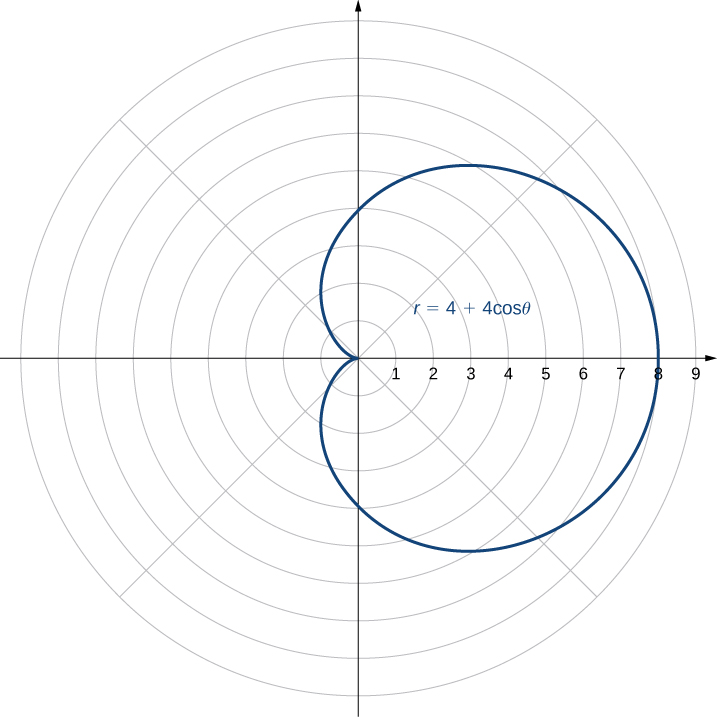
Graph the curve defined by the function ![]() Identify the curve and rewrite the equation in rectangular coordinates.
Identify the curve and rewrite the equation in rectangular coordinates.
Solution
Because the function is a multiple of a sine function, it is periodic with period ![]() so use values for
so use values for ![]() between 0 and
between 0 and ![]() The result of steps 1–3 appear in the following table.
The result of steps 1–3 appear in the following table.
| 0 | 0 | 0 | ||
| 0 |
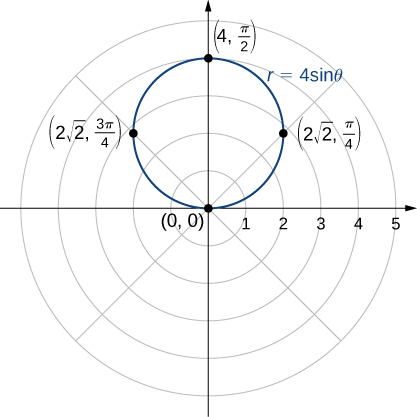
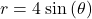 is a circle.
is a circle.This is the graph of a circle. The equation ![]() can be converted into rectangular coordinates by first multiplying both sides by
can be converted into rectangular coordinates by first multiplying both sides by ![]() This gives the equation
This gives the equation ![]() Next use the facts that
Next use the facts that ![]() and
and ![]() This gives
This gives ![]() To put this equation into standard form, subtract
To put this equation into standard form, subtract ![]() from both sides of the equation and complete the square:
from both sides of the equation and complete the square:
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill {x}^{2}+{y}^{2}-4y&\ds =\hfill &\ds 0\hfill \\[5mm]\ds \hfill {x}^{2}+\left({y}^{2}-4y\right)&\ds =\hfill &\ds 0\hfill \\[5mm]\ds \hfill {x}^{2}+\left({y}^{2}-4y+4\right)&\ds =\hfill &\ds 0+4\hfill \\[5mm]\ds \hfill {x}^{2}+{\left(y-2\right)}^{2}&\ds =\hfill &\ds 4.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-3cf2f4062475a4ceb5f8c253ad47de94_l3.png)
This is the equation of a circle with radius 2 and center ![]() in the rectangular coordinate system.
in the rectangular coordinate system.
Create a graph of the curve defined by the function ![]()
Answer
The name of this shape is a cardioid, which we will study further later in this section.
Hint
Follow the problem-solving strategy for creating a graph in polar coordinates.
Because we already know how to sketch a variety of curves in Cartesian coordinates, transforming polar equations into rectangular coordinates may help sketching some polar curves as shown in the following example.
Transforming Polar Equations to Rectangular Coordinates
Rewrite each of the following equations in rectangular coordinates and identify the graph.
Solution
- Take the tangent of both sides. This gives
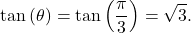 Since
Since 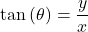 we can replace the left-hand side of this equation by
we can replace the left-hand side of this equation by 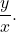 This gives
This gives 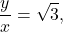 which can be rewritten as
which can be rewritten as 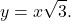 This is the equation of a straight line passing through the origin with slope
This is the equation of a straight line passing through the origin with slope 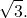 In general, any polar equation of the form
In general, any polar equation of the form 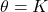 represents a straight line through the pole with slope equal to
represents a straight line through the pole with slope equal to 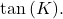
- First, square both sides of the equation. This gives
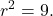 Next replace
Next replace 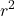 with
with 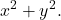 This gives the equation
This gives the equation 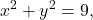 which is the equation of a circle centered at the origin with radius 3. In general, any polar equation of the form
which is the equation of a circle centered at the origin with radius 3. In general, any polar equation of the form 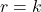 , where k is a constant, represents a circle of radius |k| centered at the origin. (Note: when squaring both sides of an equation it is possible to introduce new points unintentionally. This should always be taken into consideration. However, in this case we do not introduce new points. For example,
, where k is a constant, represents a circle of radius |k| centered at the origin. (Note: when squaring both sides of an equation it is possible to introduce new points unintentionally. This should always be taken into consideration. However, in this case we do not introduce new points. For example, 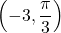 is the same point as
is the same point as 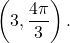 )
) - Multiply both sides of the equation by
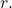 This leads to
This leads to 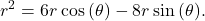 Next use the formulas
Next use the formulas
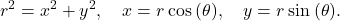
This gives
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill {r}^{2}&\ds =\hfill &\ds 6\left(r\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.2em}{0ex}}(\theta) \right)-8\left(r\phantom{\rule{0.2em}{0ex}}\text{sin}\phantom{\rule{0.2em}{0ex}}(\theta) \right)\hfill \\[5mm]\ds \hfill {x}^{2}+{y}^{2}&\ds =\hfill &\ds 6x-8y.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-848be3b433c5d6445e641bb4b9a2ba95_l3.png)
To put this equation into standard form, first move the variables from the right-hand side of the equation to the left-hand side, then complete the square.
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill {x}^{2}+{y}^{2}&\ds =\hfill &\ds 6x-8y\hfill \\[5mm]\ds \hfill {x}^{2}-6x+{y}^{2}+8y&\ds =\hfill &\ds 0\hfill \\[5mm]\ds \hfill \left({x}^{2}-6x\right)+\left({y}^{2}+8y\right)&\ds =\hfill &\ds 0\hfill \\[5mm]\ds \hfill \left({x}^{2}-6x+9\right)+\left({y}^{2}+8y+16\right)&\ds =\hfill &\ds 9+16\hfill \\[5mm]\ds \hfill {\left(x-3\right)}^{2}+{\left(y+4\right)}^{2}&\ds =\hfill &\ds 25.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-711324dc2cf5b570106da7031d8ab663_l3.png)
This is the equation of a circle with center at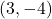 and radius 5. Notice that the circle passes through the origin since the center is 5 units away.
and radius 5. Notice that the circle passes through the origin since the center is 5 units away.
Rewrite the equation ![]() in rectangular coordinates and identify its graph.
in rectangular coordinates and identify its graph.
Answer
![]() which is the equation of a parabola opening upward.
which is the equation of a parabola opening upward.
Hint
Rewrite secant as the reciprocal of cosine and multiply both sides by cosine.
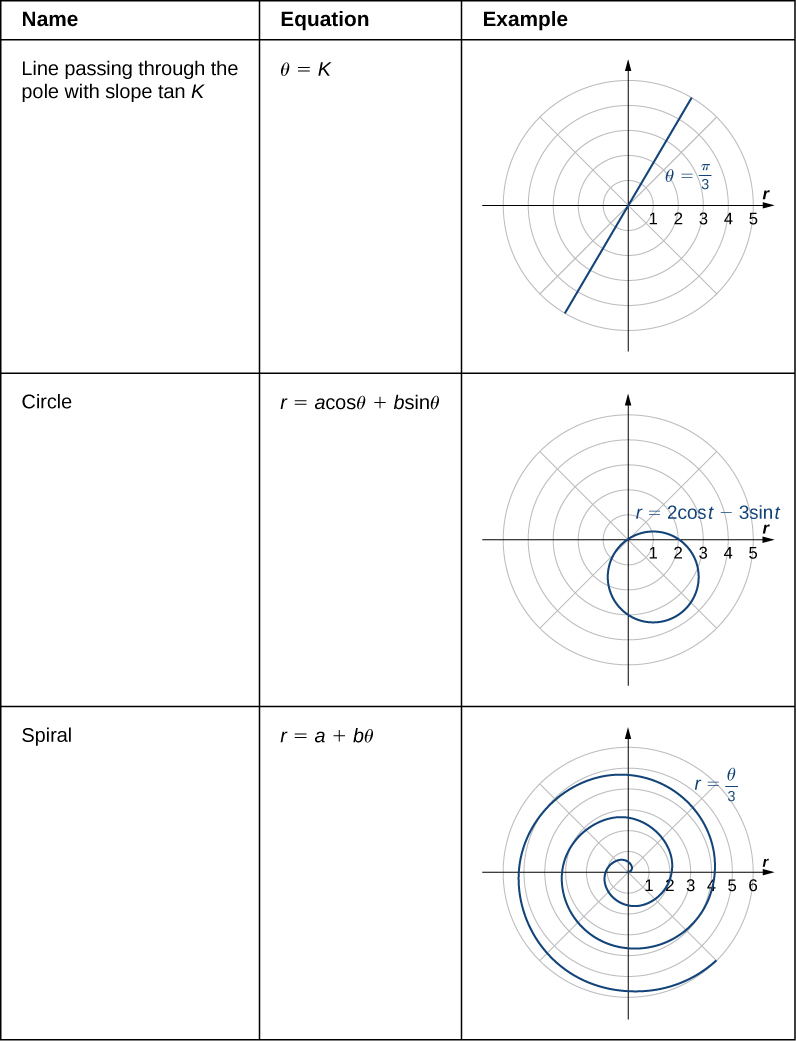
We have now seen several examples of curves defined by polar equations. A summary of some common curves is given in the table below. In each equation, a and b are arbitrary constants.
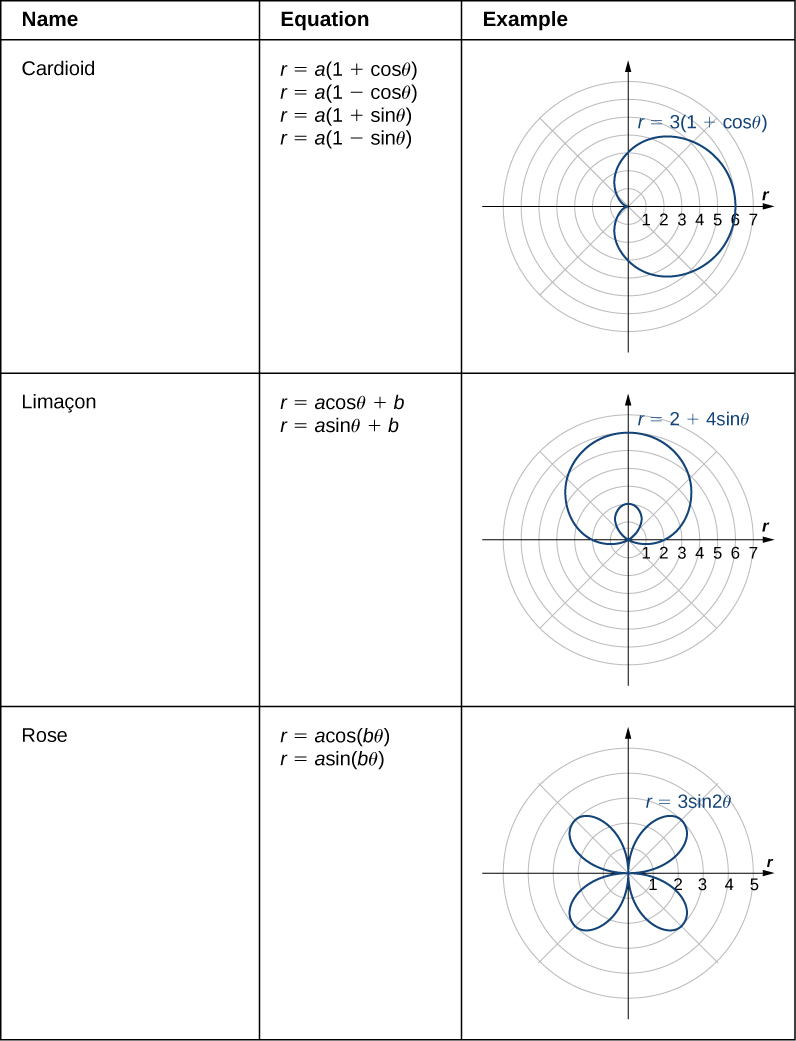
A cardioid is a special case of a limaçon (pronounced “lee-mah-son”), in which ![]() or
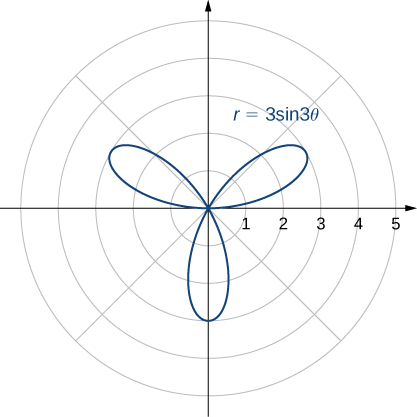
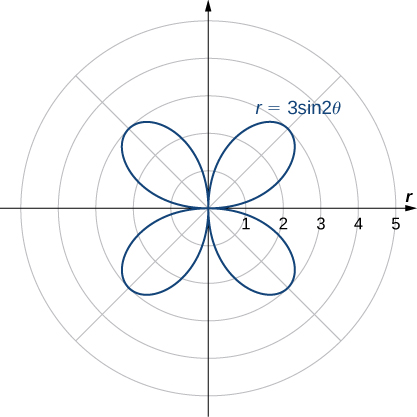
or ![]() The rose is a very interesting curve. Notice that the graph of
The rose is a very interesting curve. Notice that the graph of ![]() has four petals. However, the graph of
has four petals. However, the graph of ![]() has three petals as shown below.
has three petals as shown below.
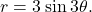
If the coefficient of ![]() is even, the graph has twice as many petals as the coefficient. If the coefficient of
is even, the graph has twice as many petals as the coefficient. If the coefficient of ![]() is odd, then the number of petals equals the coefficient. You are encouraged to explore why this happens. Even more interesting graphs emerge when the coefficient of
is odd, then the number of petals equals the coefficient. You are encouraged to explore why this happens. Even more interesting graphs emerge when the coefficient of ![]() is not an integer. For example, if it is rational, then the curve is closed; that is, it eventually ends where it started, see Figure 6 (a) below. However, if the coefficient is irrational, then the curve never closes, see Figure 6 (b). Although it may appear that the curve is closed, a closer examination reveals that the petals just above the positive x axis are slightly thicker. This is because the petal does not quite match up with the starting point.
is not an integer. For example, if it is rational, then the curve is closed; that is, it eventually ends where it started, see Figure 6 (a) below. However, if the coefficient is irrational, then the curve never closes, see Figure 6 (b). Although it may appear that the curve is closed, a closer examination reveals that the petals just above the positive x axis are slightly thicker. This is because the petal does not quite match up with the starting point.
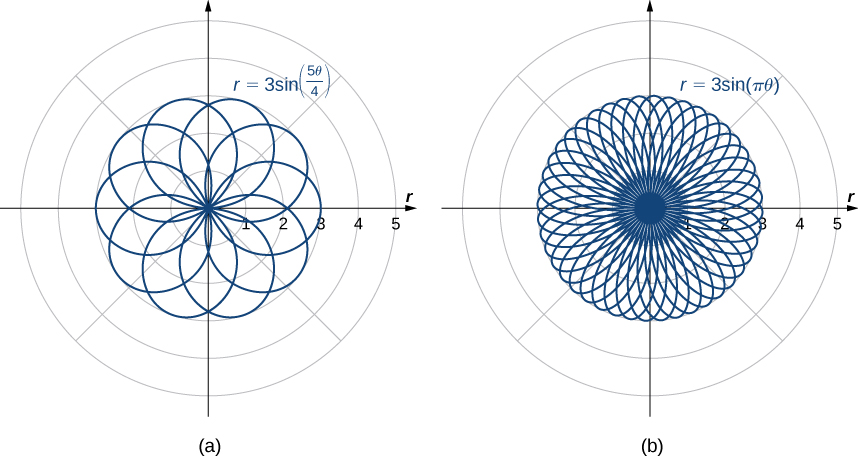
Since the curve defined by the graph of ![]() never closes, the curve shown in Figure 6 (b) is only a partial depiction. In fact, this is an example of a space-filling curve. A space-filling curve is one that in fact occupies a two-dimensional subset of the real plane. In this case, the curve occupies the circle of radius 3 centered at the origin.
never closes, the curve shown in Figure 6 (b) is only a partial depiction. In fact, this is an example of a space-filling curve. A space-filling curve is one that in fact occupies a two-dimensional subset of the real plane. In this case, the curve occupies the circle of radius 3 centered at the origin.
Chapter Opener: Describing a Spiral
Recall the chambered nautilus introduced in the chapter opener. This creature displays a spiral when half the outer shell is cut away. Figure 7 below shows a spiral in rectangular coordinates. How can we describe this curve analitically, that is, using formulas?
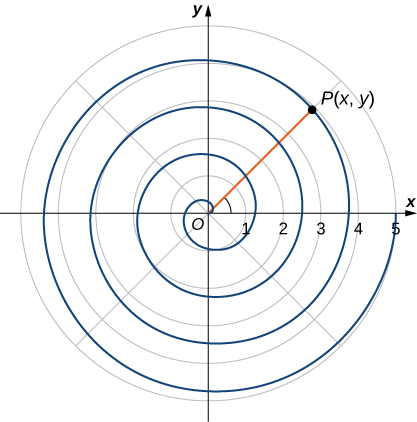
Solution
As the point P travels around the spiral in a counterclockwise direction, its distance d from the origin increases. Assume that the distance d is a constant multiple k of the angle ![]() that the line segment OP makes with the positive x-axis. Therefore
that the line segment OP makes with the positive x-axis. Therefore ![]() where
where ![]() is the origin. Now use the distance formula and some trigonometry:
is the origin. Now use the distance formula and some trigonometry:
![Rendered by QuickLaTeX.com \ds \begin{array}{ccc}\hfill d\left(P,O\right)&\ds =\hfill &\ds k\theta \hfill \\[5mm]\ds \hfill \sqrt{{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}}&\ds =\hfill &\ds k\phantom{\rule{0.2em}{0ex}}\text{arctan}\left(\frac{y}{x}\right)\hfill \\[5mm]\ds \hfill \sqrt{{x}^{2}+{y}^{2}}&\ds =\hfill &\ds k\phantom{\rule{0.2em}{0ex}}\text{arctan}\left(\frac{y}{x}\right)\hfill \\[5mm]\ds \hfill \text{arctan}\left(\frac{y}{x}\right)&\ds =\hfill &\ds \frac{\sqrt{{x}^{2}+{y}^{2}}}{k}\hfill \\[5mm]\ds \hfill y&\ds =\hfill &\ds x\phantom{\rule{0.2em}{0ex}}\text{tan}\left(\frac{\sqrt{{x}^{2}+{y}^{2}}}{k}\right).\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-5679190086f81075132c25ff3c15311a_l3.png)
Although this equation describes the spiral, it is not possible to solve it directly for either x or y. However, if we use polar coordinates, the equation becomes much simpler. In particular, ![]() and
and ![]() is the second coordinate. Therefore the equation for the spiral becomes
is the second coordinate. Therefore the equation for the spiral becomes ![]() Note that when
Note that when ![]() we also have
we also have ![]() so the spiral emanates from the origin. We can remove this restriction by adding a constant to the equation. Then the equation for the spiral becomes
so the spiral emanates from the origin. We can remove this restriction by adding a constant to the equation. Then the equation for the spiral becomes ![]() for arbitrary constants
for arbitrary constants ![]() and
and ![]() This is referred to as an Archimedean spiral, after the Greek mathematician Archimedes.
This is referred to as an Archimedean spiral, after the Greek mathematician Archimedes.
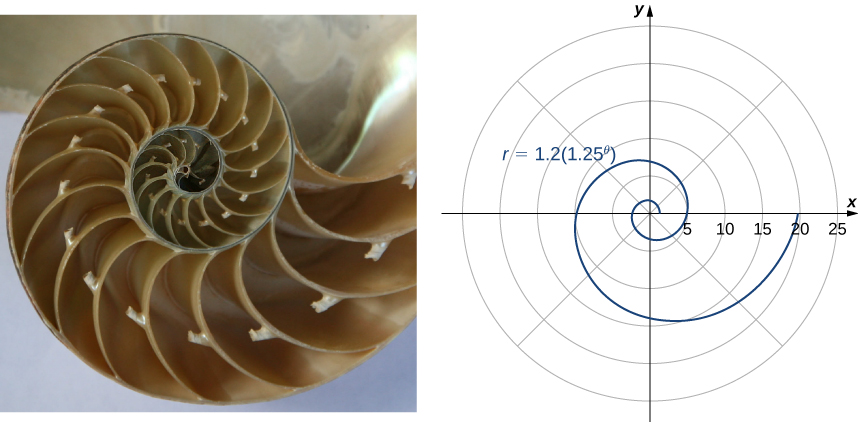
Another type of spiral is the logarithmic spiral, described by the function ![]() A graph of the function
A graph of the function ![]() is given in Figure 8 below. This spiral describes the shell shape of the chambered nautilus.
is given in Figure 8 below. This spiral describes the shell shape of the chambered nautilus.
Suppose a curve is described in the polar coordinate system via the function ![]() Since we have conversion formulas from polar to rectangular coordinates given by
Since we have conversion formulas from polar to rectangular coordinates given by ![]() we can rewrite the polar equation in Cartesian coordinates:
we can rewrite the polar equation in Cartesian coordinates:
![]()
This step gives a parameterization of the curve in rectangular coordinates using ![]() as the parameter and allows to perform calculus methods we developed in the previous section to parametric curves.
as the parameter and allows to perform calculus methods we developed in the previous section to parametric curves.
Calculus with Polar Curves
Find the slope of the tangent line to the spiral with polar equation ![]() at the point corresponding to
at the point corresponding to ![]() .
.
Solution
We first find the parametrization of the spiral in rectangular coordinates by using conversion formulas (*) and replacing ![]() with
with ![]() as was shown above:
as was shown above:
![Rendered by QuickLaTeX.com \ds \begin{array}{l} &x=r\cos(\theta)=(\pi-\theta)\cos(\theta)\hfill\\[3mm] &y=r\sin(\theta)=(\pi-\theta)\sin(\theta)\hfill\end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7bc13cfdfebe3aef984e7d62c68f7430_l3.png)
Next we find ![]() as a function of
as a function of ![]() using the methods of the previous section.
using the methods of the previous section.
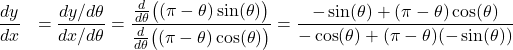
The slope ![]() of the tangent line to the spiral at the point corresponding to
of the tangent line to the spiral at the point corresponding to ![]() can be found by substituting
can be found by substituting ![]() into the above formula for
into the above formula for ![]() :
:
![Rendered by QuickLaTeX.com \ds \begin{array}{ll} \ds m&\ds=\frac{dy}{dx}\left(\frac{2\pi}3\right)=\frac{-\sin\left(\frac{2\pi}3\right)+\left(\pi-\frac{2\pi}3\right)\cos\left(\frac{2\pi}3\right)}{-\cos\left(\frac{2\pi}3\right)+\left(\pi-\frac{2\pi}3\right)\left(-\sin\left(\frac{2\pi}3\right)\right)}\hfill\\[5mm] &\ds=\frac{-\frac{\sqrt3}2+\frac{\pi}3\cdot\left(-\frac12\right)}{-\left(-\frac12\right)+\frac{\pi}3\cdot\left(-\frac{\sqrt3}2\right)} =\frac{3\sqrt3+\pi}{-3+\sqrt3\pi}.\hfill\end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-ec663a492811a520765cf6f1b4c39e30_l3.png)
Find the slope of the tangent line to the polar curve ![]() at the point corresponding to
at the point corresponding to ![]() .
.
Answer
The slope is ![]() .
.
Symmetry in Polar Coordinates
When studying symmetry of functions in rectangular coordinates (i.e., in the form ![]() ) we talk about symmetry with respect to the y-axis and symmetry with respect to the origin. In particular, if
) we talk about symmetry with respect to the y-axis and symmetry with respect to the origin. In particular, if ![]() for all
for all ![]() in the domain of
in the domain of ![]() then
then ![]() is an even function and its graph is symmetric with respect to the y-axis. If
is an even function and its graph is symmetric with respect to the y-axis. If ![]() for all
for all ![]() in the domain of
in the domain of ![]() then
then ![]() is an odd function and its graph is symmetric with respect to the origin. By determining which types of symmetry a graph exhibits, we can learn more about the shape and appearance of the graph. Symmetry can also reveal other properties of the function that generates the graph. Symmetry in polar curves works in a similar fashion.
is an odd function and its graph is symmetric with respect to the origin. By determining which types of symmetry a graph exhibits, we can learn more about the shape and appearance of the graph. Symmetry can also reveal other properties of the function that generates the graph. Symmetry in polar curves works in a similar fashion.
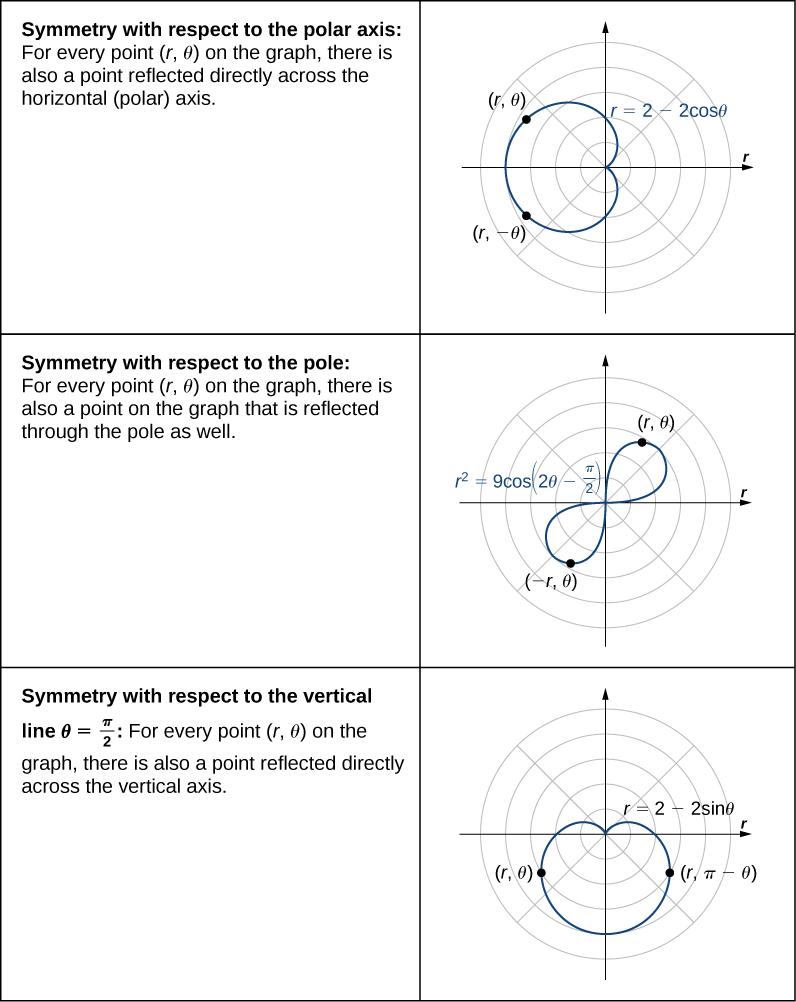
Symmetry in Polar Curves and Equations
Consider a polar curve with equation ![]() .
.
- The curve is symmetric about the polar axis if for every point
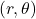 on the graph, the point
on the graph, the point 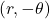 is also on the graph. This happens if
is also on the graph. This happens if 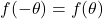 or
or 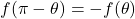 .
. - The curve is symmetric about the pole if for every point
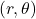 on the graph, the point
on the graph, the point 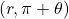 is also on the graph. This happens if
is also on the graph. This happens if 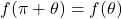 .
. - The curve is symmetric about the vertical line
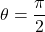 if for every point
if for every point 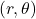 on the graph, the point
on the graph, the point 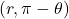 is also on the graph. This happens if
is also on the graph. This happens if 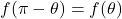 or
or 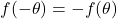 .
.
The following table shows examples of each type of symmetry.
Using Symmetry to Graph a Polar Equation
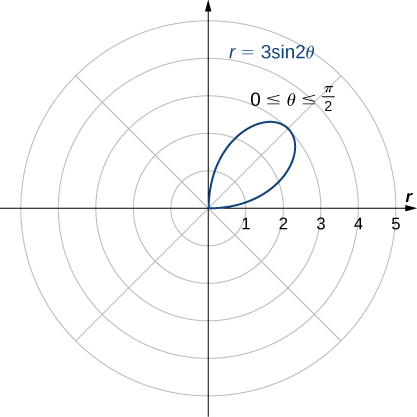
Determine all symmetries of the rose defined by the equation ![]() and create a graph.
and create a graph.
Solution
Suppose the point ![]() is on the graph of
is on the graph of ![]()
Let ![]() . We first substitute
. We first substitute ![]() instead of
instead of ![]() into
into ![]() :
:
![]() ,
,
since sine is an odd function. According to iii in the statement above, this implies symmetry with respect to the vertical line ![]() .
.
To test for symmetry with respect to the polar axis, we consider ![]() :
:
![]() ,
,
since sine function is ![]() -periodic and odd. Hence, by i, we have that the curve is symmetric with respect to the polar axis as well.
-periodic and odd. Hence, by i, we have that the curve is symmetric with respect to the polar axis as well.
Geometrically, the above two symmetries automatically imply symmetry with respect to the pole, but this can also be verified analytically by checking that ![]() .
.
So this graph has symmetry with respect to the vertical line going through the pole, the polar axis and the origin. To sketch the curve, tabulate values of ![]() between 0 and
between 0 and ![]() and then reflect the resulting graph about the polar axis and the line
and then reflect the resulting graph about the polar axis and the line ![]() .
.
This gives one petal of the rose, as shown in the following figure.
 and
and 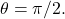
Reflecting this image into the other three quadrants gives the entire graph as shown below.
Determine all symmetries of the polar curve ![]() and create a graph.
and create a graph.
Answer
Symmetric with respect to the polar axis.
Key Concepts
- The polar coordinate system provides an alternative way to locate points in the plane.
- Convert points between rectangular and polar coordinates using the formulas
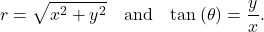
- To sketch a polar curve, make a table of values and take advantage of periodic properties.
- Use the conversion formulas to convert equations between rectangular and polar coordinates.
- Identify symmetry in polar curves, which can occur through the pole, the horizontal axis, or the vertical axis.
Exercises
In the following exercises, plot the point whose polar coordinates are given by first constructing the angle ![]() and then marking off the distance r along the ray.
and then marking off the distance r along the ray.
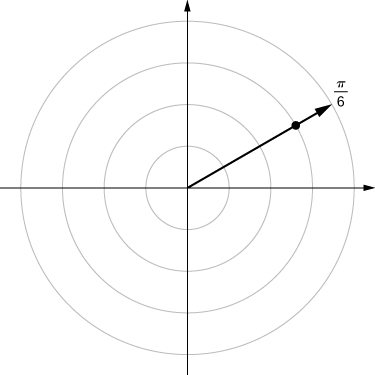
1. ![]()
Answer
2. ![]()
3. ![]()
Answer
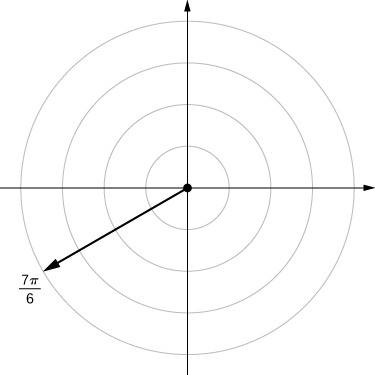
4. ![]()
5. ![]()
Answer
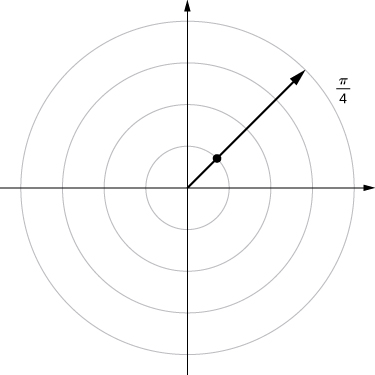
6. ![]()
7. ![]()
Answer
For the following exercises, consider the polar graph below. Give two sets of polar coordinates for each point.
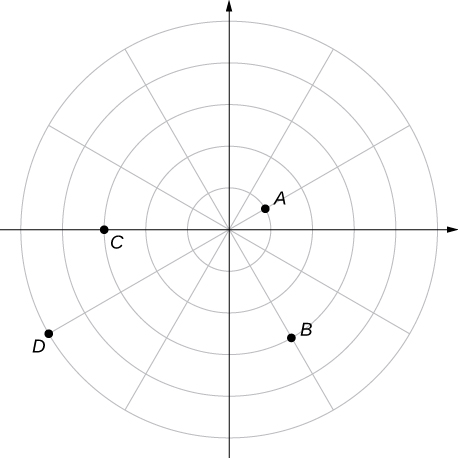
8. Point A.
9. Point B.
Answer
![]()
10. Point C.
11. Point D.
Answer
![]()
For the following exercises, the rectangular coordinates of a point are given. Find two sets of polar coordinates for the point with the angular coordinate ![]() in
in ![]()
12. ![]()
13. ![]()
Answer
![]()
14. ![]()
15. ![]()
Answer
![]()
16. ![]()
17. ![]()
Answer
![]()
For the following exercises, find rectangular coordinates for the given point in polar coordinates.
18. ![]()
19. ![]()
Answer
![]()
20. ![]()
21. ![]()
Answer
22. ![]()
23. ![]()
Answer
![]()
24. ![]()
(There is no typo in this question.)
For the following exercises, determine the shape of each polar curve.
25. ![]()
Answer
Circle.
26. ![]()
27. ![]()
Answer
Spiral.
For the following exercises, convert the polar equation to rectangular form and sketch its graph.
28. ![]()
29. ![]()
Answer
![]()
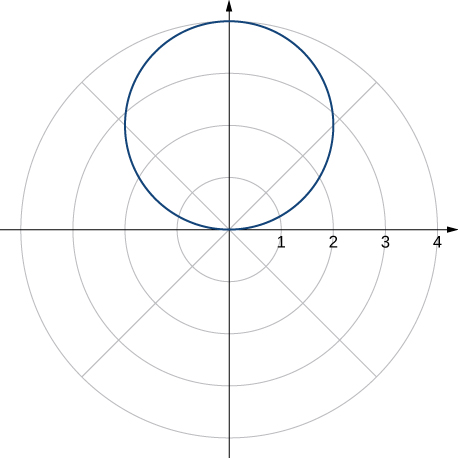
30. ![]()
31. Consider polar curve ![]() . Then
. Then ![]() and
and ![]() are parametric equations of the curve in rectangular coordinates. Using calculus for parametric curves, derive the formula for the derivative
are parametric equations of the curve in rectangular coordinates. Using calculus for parametric curves, derive the formula for the derivative ![]() of a polar equation.
of a polar equation.
Answer
![]()
For the following exercises, find the slope of the tangent line to the given polar curve at the point that corresponds to the specified value of angular coordinate ![]() .
.
32. ![]()
33. ![]()
Answer
The slope is ![]()
34. ![]()
35. ![]()
Answer
The slope is ![]() .
.
36. ![]()
37. ![]()
Answer
The slope is ![]() .
.
For the following exercises, find the Cartesian coordinates of the points at which the following polar curves have horizontal or vertical tangent line.
38. ![]()
39.* The cardioid ![]()
(Hint: if for some ![]() both
both ![]() and
and ![]() , one needs to consider
, one needs to consider ![]() to determine if the tangent line at the corresponding point is horizontal, vertical, or neither.)
to determine if the tangent line at the corresponding point is horizontal, vertical, or neither.)
Answer
Horizontal tangents at 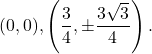 Vertical tangents at
Vertical tangents at 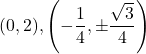 .
.
40. Find all points on the polar curve ![]() , where the tangent line is horizontal.
, where the tangent line is horizontal.
For the following exercises, determine whether the polar curves are symmetric with respect to the polar axis, the pole, or the vertical line ![]() through the pole.
through the pole.
41. ![]()
Answer
Symmetric with respect to the polar axis, the pole, and the vertical line ![]() .
.
42. ![]()
43. ![]()
Answer
Symmetric with respect to the polar axis only.
44. ![]()
45. ![]()
Answer
Symmetry with respect to the vertical line ![]() only.
only.
For the following exercises, identify any symmetries of a given polar curve and then sketch it.
46. ![]()
47. ![]()
Answer
Symmetric with respect to the vertical line ![]() .
.
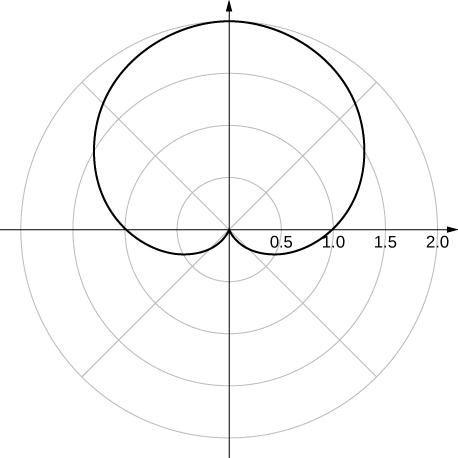
48. ![]()
49. ![]()
Answer
Symmetric with respect to the vertical line ![]() .
.
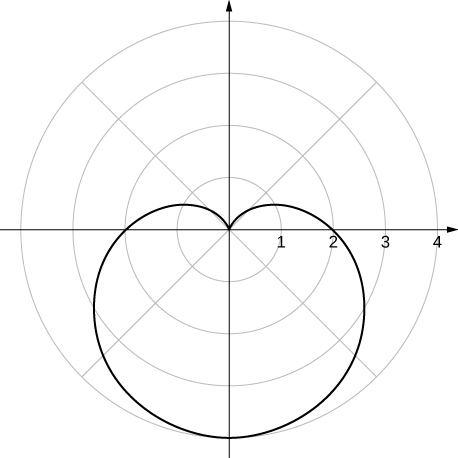
50. ![]()
51. ![]()
Answer
Symmetric with respect to the pole, the polar axis and the vertical line ![]() .
.
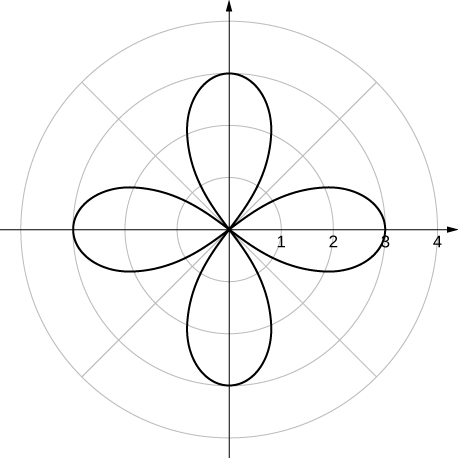
52. ![]()
53. ![]()
Answer
Symmetric with respect to the polar axis.
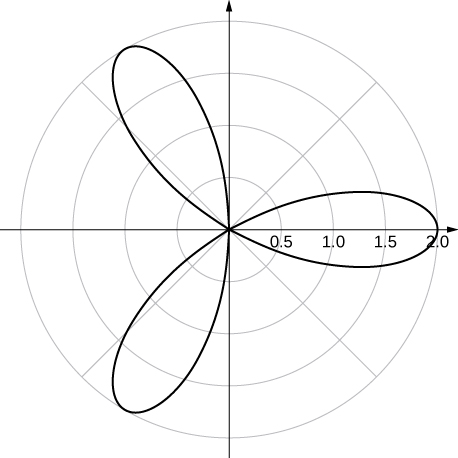
54. ![]()
55. ![]()
Answer
Symmetric with respect to the pole, the polar axis and the vertical line ![]() .
.
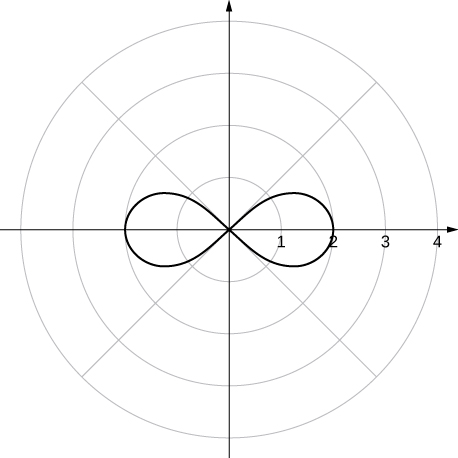
56. ![]()
57. ![]() ,
, ![]()
Answer
No symmetries.
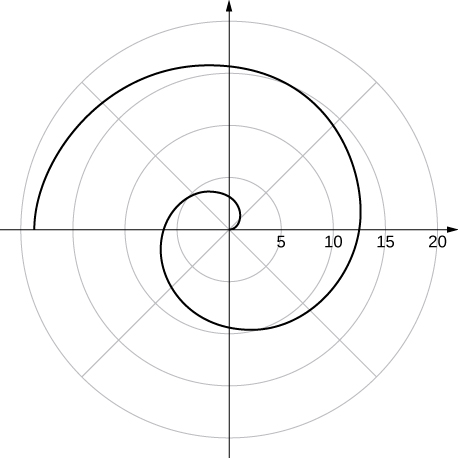
58. [T] The graph of ![]() is called a strophoid. Use a graphing utility to sketch the graph, and, from the graph, determine the asymptote.
is called a strophoid. Use a graphing utility to sketch the graph, and, from the graph, determine the asymptote.
59. [T] Use a graphing utility and sketch the graph of ![]()
Answer
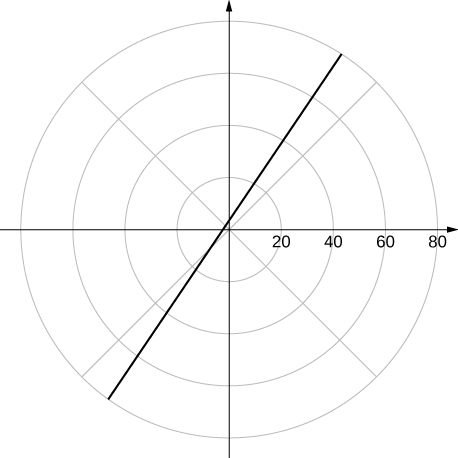
60. [T] Use a graphing utility to graph ![]()
61. [T] Use technology to graph ![]()
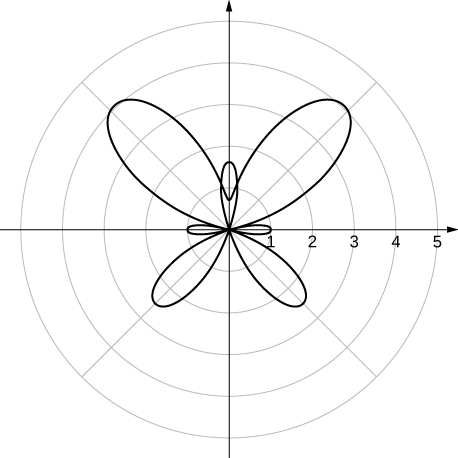
Answer
62. [T] Use technology to plot ![]() (use the interval
(use the interval ![]()
63. [T] Use technology to plot ![]() for
for ![]()
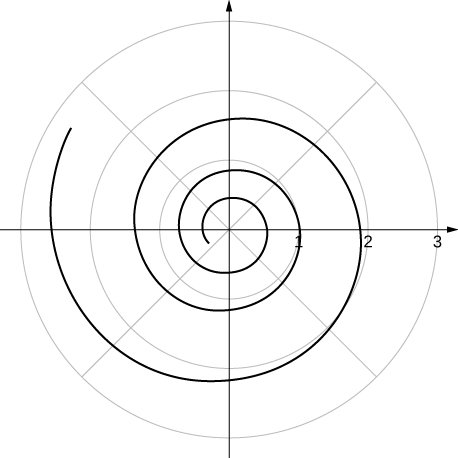
Answer
64. [T] There is a curve known as the “Black Hole.” Use technology to plot ![]() for
for ![]()
Glossary
- angular coordinate
 the angle formed by a line segment connecting the origin to a point in the polar coordinate system with the positive radial (x) axis, measured counterclockwise
the angle formed by a line segment connecting the origin to a point in the polar coordinate system with the positive radial (x) axis, measured counterclockwise
- cardioid
- a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius; the equation of a cardioid is
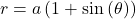 or
or 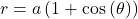
- limaçon
- the graph of the equation
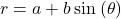 or
or 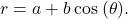 If
If 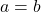 then the graph is a cardioid
then the graph is a cardioid
- polar axis
- the horizontal axis in the polar coordinate system corresponding to
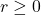
- polar coordinate system
- a system for locating points in the plane. The coordinates are
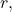 the radial coordinate, and
the radial coordinate, and 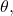 the angular coordinate
the angular coordinate
- polar equation
- an equation or function relating the radial coordinate to the angular coordinate in the polar coordinate system
- pole
- the central point of the polar coordinate system, equivalent to the origin of a Cartesian system
- radial coordinate
 the coordinate in the polar coordinate system that measures the distance from a point in the plane to the pole
the coordinate in the polar coordinate system that measures the distance from a point in the plane to the pole
- rose
- graph of the polar equation
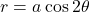 or
or 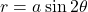 for a positive constant a
for a positive constant a
- space-filling curve
- a curve that completely occupies a two-dimensional subset of the real plane

