3.2 Trigonometric Integrals
Learning Objectives
- Solve integration problems involving products of powers of
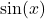 and
and 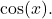
- Integrate products of sines and cosines of different angles.
- Solve integration problems involving products of powers of
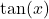 and
and 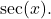
- Use reduction formulas to evaluate trigonometric integrals.
In this section we look at how to integrate a variety of products of trigonometric functions. These integrals are called trigonometric integrals. They are an important part of the integration technique called trigonometric substitution used for integrating functions involving certain root expressions that will be discussed in the next section. In addition, these types of integrals appear frequently when we study polar, cylindrical, and spherical coordinate systems later. Let’s begin our study with products of powers of ![]() and
and ![]()
Integrating Products and Powers of sin(x) and cos(x)
A key idea behind the strategy used to integrate combinations of powers of ![]() and
and ![]() involves rewriting these expressions as sums and differences of integrals of the form
involves rewriting these expressions as sums and differences of integrals of the form ![]() or
or ![]() that can be evaluated using u-substitution. Before describing the general process in detail, let’s take a look at the following examples.
that can be evaluated using u-substitution. Before describing the general process in detail, let’s take a look at the following examples.
Evaluating 
Evaluate ![]()
Solution
Make a substitution ![]() In this case,
In this case, ![]() Thus,
Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds {\int }^{}{\text{cos}}^{3}\phantom{\rule{0.2em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds = - {\int }^{}{u}^{3}\phantom{\rule{0.2em}{0ex}}du\hfill \\[5mm]\ds \hfill &\ds =-\frac{1}{4}{u}^{4}+C\hfill \\[5mm]\ds \hfill &\ds =-\frac{1}{4}{\text{cos}}^{4}\phantom{\rule{0.2em}{0ex}}(x)+C.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-d61c8eab3768ac60b97a56dc0114f8b7_l3.png)
Evaluate ![]()
Answer
![]()
Hint
Take ![]()
A Preliminary Example: Evaluating  When
When 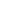 is Odd
is Odd
Evaluate ![]()
Solution
To convert this integral into a combination of integrals the form ![]() rewrite
rewrite ![]()
We now make a substitution ![]() , which means that
, which means that ![]() , and obtain
, and obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds {\int }^{}{\text{cos}}^{2}(x)\phantom{\rule{0.1em}{0ex}}{\text{sin}}^{3}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds ={\int }^{}{\text{cos}}^{2}(x)\left(1-{\text{cos}}^{2}(x)\right)\text{sin}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill \\[5mm]\ds \hfill &\ds = - {\int }^{}{u}^{2}\left(1-{u}^{2}\right)du\hfill \\[5mm]\ds \hfill &\ds ={\int }^{}\left({u}^{4}-{u}^{2}\right)du\hfill \\[5mm]\ds \hfill &\ds =\frac{1}{5}{u}^{5}-\frac{1}{3}{u}^{3}+C\hfill \\[5mm]\ds \hfill &\ds =\frac{1}{5}{\text{cos}}^{5}(x)-\frac{1}{3}{\text{cos}}^{3}(x)+C.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-cfda080d7f0548dc20bcb5d4b84d437f_l3.png)
Evaluate ![]()
Answer
![]()
Hint
Write ![]() and let
and let ![]()
In the next example, we see the strategy that must be applied when there are only even powers of ![]() and
and ![]() For integrals of this type, the identities
For integrals of this type, the identities
![]() and
and
![]()
are invaluable. These identities are sometimes known as power-reducing identities and they may be derived from the double-angle identity ![]() and the Pythagorean identity
and the Pythagorean identity ![]()
Integrating an Even Power of 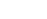
Evaluate ![]()
Solution
To evaluate this integral, let’s use the trigonometric identity ![]() Thus,
Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds {\int }^{}{\text{sin}}^{2}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds ={\int }^{}\left(\frac{1}{2}-\frac{1}{2}\text{cos}\left(2x\right)\right)\,dx \hfill \\[5mm]\ds \hfill &\ds =\frac{1}{2}x-\frac{1}{4}\text{sin}\left(2x\right)+C.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7a709555de98097fa817529fd244311e_l3.png)
Evaluate ![]()
Answer
![]()
Hint
The general process for integrating products of powers of ![]() and
and ![]() is summarized in the following set of guidelines.
is summarized in the following set of guidelines.
Problem-Solving Strategy: Integrating Products of Powers of sin(x) and cos(x)
To evaluate ![]() use the following strategies:
use the following strategies:
- If
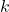 is odd, rewrite
is odd, rewrite 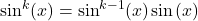 and use the identity
and use the identity 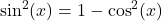 to rewrite
to rewrite 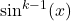 in terms of
in terms of 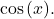 Integrate using the substitution
Integrate using the substitution 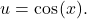 This substitution makes
This substitution makes 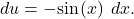
- If
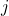 is odd, rewrite
is odd, rewrite 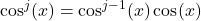 and use the identity
and use the identity 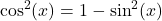 to rewrite
to rewrite 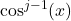 in terms of
in terms of 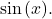 Integrate using the substitution
Integrate using the substitution 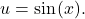 This substitution makes
This substitution makes 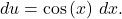
(Note: If both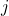 and
and 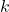 are odd, either strategy 1 or strategy 2 may be used.)
are odd, either strategy 1 or strategy 2 may be used.) - If both
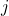 and
and 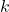 are even, use identities
are even, use identities 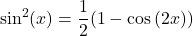 and
and 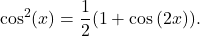 After applying these formulas, simplify and reapply strategies 2 and 3 to the combination of powers of
After applying these formulas, simplify and reapply strategies 2 and 3 to the combination of powers of  as appropriate.
as appropriate.
Evaluating  When
When 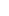 is Odd
is Odd
Evaluate ![]()
Solution
Since the power on ![]() is odd, use strategy 2.
is odd, use strategy 2.
![Rendered by QuickLaTeX.com \ds \begin{array}{cccc}\hfill\ds{\int }^{}{\text{cos}}^{5}(x)\phantom{\rule{0.1em}{0ex}}{\text{sin}}^{8}(x)\phantom{\rule{0.2em}{0ex}}\,dx &\ds ={\int }^{}{\text{cos}}^{4}(x)\phantom{\rule{0.1em}{0ex}}{\text{sin}}^{8}(x)\phantom{\rule{0.1em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds &\ds \text{Break off}\phantom{\rule{0.2em}{0ex}}\text{cos}\phantom{\rule{0.1em}{0ex}}(x).\hfill \\[5mm]\ds &\ds ={\int }^{}{\left({\text{cos}}^{2}(x)\right)}^{2}\sin^8(x)\text{cos}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds &\ds \text{Rewrite}\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{4}(x)={\left({\text{cos}}^{2}(x)\right)}^{2}.\hfill \\[5mm]\ds &\ds ={\int }^{}{\left(1-{\text{sin}}^{2}(x)\right)}^{2}\sin^8(x)\text{cos}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}{\text{cos}}^{2}(x)=1-{\text{sin}}^{2}(x).\hfill \\[5mm]\ds &\ds ={\int }^{}{\left(1-{u}^{2}\right)}^{2}u^8\,du\hfill &\ds &\ds \text{Let}\phantom{\rule{0.2em}{0ex}}u=\text{sin}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}du= \text{cos}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx .\hfill \\[5mm]\ds &\ds ={\int }^{}\left( {u}^{8}-2{u}^{10}+{u}^{12}\right)du\hfill &\ds &\ds \text{Expand}.\hfill \\[5mm]\ds &\ds =\frac{1}{9}{u}^{9}-\frac{2}{11}{u}^{11}+\frac{1}{13}{u}^{13}+C\hfill &\ds &\ds \text{Evaluate the integral}.\hfill \\[5mm]\ds &\ds =\frac{1}{9}{\text{sin}}^{9}(x)-\frac{2}{11}{\text{sin}}^{11}(x)+\frac{1}{13}{\text{sin}}^{13}(x)+C.\hfill &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}u=\text{sin}\phantom{\rule{0.1em}{0ex}}(x).\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-d10d9d5d093da661b7c8ef874b993062_l3.png)
Evaluating  When
When 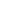 and
and 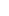 are Even
are Even
Evaluate ![]()
Solution
Since both the powers of ![]() and
and ![]() are even
are even ![]() we must use strategy 3. Thus,
we must use strategy 3. Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{cccc}\hfill \ds{\int }^{}{\text{sin}}^{4}(x)\phantom{\rule{0.2em}{0ex}}\,dx &\ds ={\int }^{}{\left({\text{sin}}^{2}(x)\right)}^{2}\,dx \hfill &\ds &\ds \text{Rewrite}\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{4}(x)={\left({\text{sin}}^{2}(x)\right)}^{2}.\hfill \\[5mm]\ds &\ds ={\int }^{}{\left(\frac{1}{2}-\frac{1}{2}\text{cos}\left(2x\right)\right)}^{2}\,dx \hfill &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}{\text{sin}}^{2}(x)=\frac{1}{2}-\frac{1}{2}\text{cos}\left(2x\right).\hfill \\[5mm]\ds &\ds ={\int }^{}\left(\frac{1}{4}-\frac{1}{2}\text{cos}\left(2x\right)+\frac{1}{4}{\text{cos}}^{2}\left(2x\right)\right)\,dx \hfill &\ds &\ds \text{Expand}\phantom{\rule{0.1em}{0ex}}{\left(\frac{1}{2}-\frac{1}{2}\text{cos}\left(2x\right)\right)}^{2}.\hfill \ds &\ds \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-5b468d729c4f2981df11d5dca3e89b88_l3.png)
Since ![]() has an even power, we use strategy 3 again and substitute
has an even power, we use strategy 3 again and substitute ![]() to continue the equalities as follows:
to continue the equalities as follows:
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds={\int }^{}\left(\frac{1}{4}-\frac{1}{2}\text{cos}\left(2x\right)+\frac{1}{4}\left(\frac{1}{2}+\frac{1}{2}\text{cos}\left(4x\right)\right)\right)\,dx \hfill &\hfill\\[5mm]\ds={\int }^{}\left(\frac{3}{8}-\frac{1}{2}\text{cos}\left(2x\right)+\frac{1}{8}\text{cos}\left(4x\right)\right)\,dx \hfill &\ds \text{Simplify}.\hfill \\[5mm]\ds =\frac{3}{8}x-\frac{1}{4}\text{sin}\left(2x\right)+\frac{1}{32}\phantom{\rule{0.1em}{0ex}}\text{sin}\left(4x\right)+C.\hfill &\ds \text{Evaluate the integral}.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-4482f5e32a1996244d3435d5d66ae42a_l3.png)
Evaluate ![]()
Answer
![]()
Hint
Use strategy 2. Write ![]() and substitute
and substitute ![]()
Evaluate ![]()
Answer
![]()
Hint
Use strategy 3 and substitute ![]() .
.
In some areas of physics, such as quantum mechanics, signal processing, and the computation of Fourier series, it is often necessary to integrate products that include ![]()
![]()
![]() and
and ![]() These integrals are evaluated by applying trigonometric identities, as outlined below.
These integrals are evaluated by applying trigonometric identities, as outlined below.
Integrating Products of Sines and Cosines of Different Angles
To integrate products involving ![]()
![]()
![]() and
and ![]() use the following identities
use the following identities
![Rendered by QuickLaTeX.com \ds \begin{array}{ll}\text{sin}\left(ax\right)\text{sin}\left(bx\right)&=\ds\frac{1}{2}\text{cos}\big(\left(a-b\right)x\big)-\frac{1}{2}\text{cos}\big(\left(a+b\right)x\big)\hfill\\[5mm]\ds \text{sin}\left(ax\right)\text{cos}\left(bx\right) &\ds=\frac{1}{2}\text{sin}\big(\left(a-b\right)x\big)+\frac{1}{2}\text{sin}\big(\left(a+b\right)x\big)\hfill\\[5mm]\ds \text{cos}\left(ax\right)\text{cos}\left(bx\right)&\ds=\frac{1}{2}\text{cos}\big(\left(a-b\right)x\big)+\frac{1}{2}\text{cos}\big(\left(a+b\right)x\big)\hfill\end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-53249903f47e413d9387c20a98f433ed_l3.png)
These formulas may be derived from the sum-of-angle formulas for sine and cosine.
Evaluating 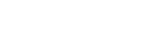
Evaluate ![]()
Solution
Apply the identity ![]() Thus,
Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds {\int }^{}\text{sin}\left(5x\right)\text{cos}\left(3x\right)\,dx \hfill &\ds ={\int }^{}\left(\frac{1}{2}\text{sin}\left(2x\right)+\frac{1}{2}\text{sin}\left(8x\right)\right)\,dx \hfill \\[5mm]\ds \hfill &\ds =-\frac{1}{4}\text{cos}\left(2x\right)-\frac{1}{16}\phantom{\rule{0.1em}{0ex}}\text{cos}\left(8x\right)+C.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7b18ac3c167135bf408a6fe083d5d9bd_l3.png)
Evaluate ![]()
Answer
![]()
Hint
Rewrite ![]()
Integrating Products and Powers of tan(x) and sec(x)
Before discussing the integration of products of powers of ![]() and
and ![]() it is useful to recall the integrals involving
it is useful to recall the integrals involving ![]() and
and ![]() we have already learned:
we have already learned:
(Formulas 1 and 2 come directly from the table of indefinite integrals, while formulas 3 and 4 were derived in Section 1.5 Substitution.)
For most integrals of products of powers of ![]() and
and ![]() we rewrite the expression we wish to integrate as the sum or difference of integrals of the form
we rewrite the expression we wish to integrate as the sum or difference of integrals of the form ![]() or
or ![]() As we see in the following example, we can evaluate these new integrals by using appropriate substitution.
As we see in the following example, we can evaluate these new integrals by using appropriate substitution.
Evaluating 
Evaluate ![]()
Solution
Start by rewriting ![]() as
as ![]() If we now let
If we now let ![]() , then
, then ![]() , and so
, and so
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds{\int }^{}{\text{sec}}^{5}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}dx &\ds ={\int }^{}{\text{sec}}^{4}(x)\phantom{\rule{0.1em}{0ex}}\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}dx \hfill \\[5mm]\ds &\ds ={\int }^{}{u}^{4}\,du\hfill \\[5mm]\ds &\ds =\frac{1}{5}{u}^{5}+C\hfill \\[5mm]\ds &\ds =\frac{1}{5}{\text{sec}}^{5}(x)+C.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-9e19d0ddbbcecb855766ffb9631bba15_l3.png)
Evaluate ![]()
Answer
![]()
Hint
Let ![]() and
and ![]()
We now take a look at the various strategies for integrating products of powers of ![]() and
and ![]()
Problem-Solving Strategy: Evaluating 
To evaluate ![]() use the following strategies:
use the following strategies:
- If
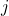 is even and
is even and 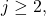 rewrite
rewrite 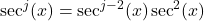 and use
and use 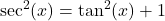 to rewrite
to rewrite 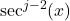 in terms of
in terms of 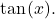 Let
Let 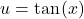 and
and 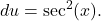
- If
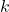 is odd and
is odd and 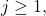 rewrite
rewrite 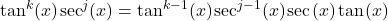 and use
and use 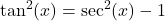 to express
to express 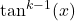 in terms of
in terms of 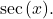 Let
Let 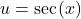 and
and 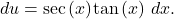
(Note: If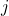 is even and
is even and 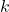 is odd, then either strategy 1 or strategy 2 may be used.)
is odd, then either strategy 1 or strategy 2 may be used.) - If
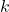 is even and
is even and 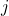 is odd, then use
is odd, then use 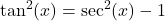 to express
to express 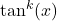 in terms of
in terms of 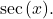 Use integration by parts to integrate odd powers of
Use integration by parts to integrate odd powers of 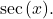
Evaluating  When
When 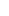 is Even
is Even
Evaluate ![]()
Solution
Since the power on ![]() is even, rewrite
is even, rewrite ![]() and use
and use ![]() to express the first
to express the first ![]() in terms of
in terms of ![]() We now make a substitution
We now make a substitution ![]() , in which case
, in which case ![]() , and we obtain
, and we obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds{\int }^{}{\text{tan}}^{6}(x)\phantom{\rule{0.1em}{0ex}}{\text{sec}}^{4}(x)\phantom{\rule{0.2em}{0ex}}\,dx &\ds ={\int }^{}{\text{tan}}^{6}(x)\left({\text{tan}}^{2}(x)+1\right){\text{sec}}^{2}(x)\hfill \\[5mm]\ds &\ds ={\int }^{}{u}^{6}\left({u}^{2}+1\right)du\hfill \\[5mm]\ds &\ds ={\int }^{}\left({u}^{8}+{u}^{6}\right)du\hfill \\[5mm]\ds &\ds =\frac{1}{9}{u}^{9}+\frac{1}{7}{u}^{7}+C\hfill \\[5mm]\ds &\ds =\frac{1}{9}{\text{tan}}^{9}(x)+\frac{1}{7}{\text{tan}}^{7}(x)+C.\hfill &\ds &\ds \hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-0f261d37cd8a4e1ab92428318d91d09f_l3.png)
Evaluating  When
When 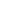 is Odd
is Odd
Evaluate ![]()
Solution
Since the power of ![]() is odd, we begin by rewriting
is odd, we begin by rewriting ![]() We then notice that
We then notice that ![]() , and make a substitution
, and make a substitution ![]() with
with ![]() . With this, we obtain
. With this, we obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds \hfill {\int }^{}{\text{tan}}^{5}(x)\phantom{\rule{0.1em}{0ex}}{\text{sec}}^{3}(x)\phantom{\rule{0.2em}{0ex}}\,dx &\ds =\ds {\int }^{}{\left(\sec^2(x)-1\right)}^{2}{\text{sec}}^{2}(x)\phantom{\rule{0.1em}{0ex}}\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill \\[5mm]\ds &\ds = {\int }^{}{\left({u}^{2}-1\right)}^{2}{u}^{2}du\hfill \\[5mm]\hfill &=\ds {\int }^{}\left({u}^{6}-2{u}^{4}+{u}^{2}\right)du\hfill \\[5mm]\ds &\ds = \frac{1}{7}{u}^{7}-\frac{2}{5}{u}^{5}+\frac{1}{3}{u}^{3}+C\hfill \\[5mm]\ds &\ds =\frac{1}{7}{\text{sec}}^{7}(x)-\frac{2}{5}{\text{sec}}^{5}(x)+\frac{1}{3}{\text{sec}}^{3}(x)+C.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-83f0f1c6f5856564ba3178e848a1c4a6_l3.png)
Evaluating 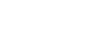
Evaluate ![]()
Solution
Although there is no ![]() under the integral, we can still use the strategy outlined above for the case when the power
under the integral, we can still use the strategy outlined above for the case when the power ![]() of
of ![]() is odd. For this, we will need to multiply and divide the integrand by
is odd. For this, we will need to multiply and divide the integrand by ![]() :
:
![Rendered by QuickLaTeX.com \begin{array}{cc}\ds {\text{tan}}^{3}(x)&=\dfrac{\sec(x){\text{tan}}^3(x)}{\sec(x)}=\dfrac1{\sec(x)}\tan^3(x)\sec(x)\hfill\\[3mm]\ds&=\dfrac{1}{\sec(x)}\tan^2(x)\sec(x)\tan(x)=\dfrac{\sec^2(x)-1}{\sec(x)}\sec(x)\tan(x).\hfill\\&\hfill\end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-2e53537852255754f51462d91f17076b_l3.png)
Hence, using the substitution ![]() , we obtain
, we obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds {\int }^{}{\text{tan}}^{3}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds ={\int }^{}\dfrac{\sec^2(x)-1}{\sec(x)}\sec(x)\tan(x)\,dx \hfill \\[5mm]\ds \hfill &\ds ={\int }^{}\dfrac{u^2-1}{u}\,du={\int }^{}\left(u-\dfrac1u\right)\,du \hfill \\[5mm]\ds \hfill &\ds =\dfrac12 u^2-\ln|u|+C=\frac{1}{2}{\text{sec}}^{2}(x)-\text{ln}|\text{sec}\phantom{\rule{0.1em}{0ex}}(x)|+C.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-0ff0556e4bcea0404019b9776d375612_l3.png)
Evaluating 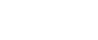
Integrate ![]()
Solution
This integral requires integration by parts. Let ![]() and
and ![]() These choices make
These choices make ![]() and
and ![]() Thus,
Thus,
![Rendered by QuickLaTeX.com \ds \begin{array}{cccc}\hfill \ds{\int }^{}{\text{sec}}^{3}(x)\phantom{\rule{0.2em}{0ex}}\,dx &\ds =\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)-{\int }^{}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds &\ds \\[5mm]\ds &\ds =\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)-{\int }^{}{\text{tan}}^{2}(x)\phantom{\rule{0.1em}{0ex}}\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds &\ds \text{Simplify}.\hfill \\[5mm]\ds &\ds =\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)-{\int }^{}\left({\text{sec}}^{2}(x)-1\right)\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds &\ds \text{Substitute}\phantom{\rule{0.2em}{0ex}}{\text{tan}}^{2}(x)={\text{sec}}^{2}(x)-1.\hfill \\[5mm]\ds &\ds =\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)+{\int }^{}\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx -{\int }^{}{\text{sec}}^{3}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds &\ds \text{Rewrite}.\hfill \\[5mm]\ds &\ds =\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)+\text{ln}|\text{sec}\phantom{\rule{0.1em}{0ex}}(x)+\text{tan}\phantom{\rule{0.1em}{0ex}}(x)|-{\int }^{}{\text{sec}}^{3}(x)\phantom{\rule{0.2em}{0ex}}\,dx .\hfill &\ds &\ds \text{Evaluate}{\int }^{}\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx .\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-05e6f307cc4ad9be074049adab5a07de_l3.png)
We now have
![]()
We see that the last integral is the same as the original one. Let ![]() be a particular antiderivative of
be a particular antiderivative of ![]() . Substituting
. Substituting ![]() instead of
instead of ![]() into the above equality, we get the following equation for
into the above equality, we get the following equation for ![]() .
.
![]() .
.
Adding ![]() to both sides, we obtain
to both sides, we obtain
![]()
Dividing by 2, we arrive at
![]()
Since an indefinite integral can be found by adding an arbitrary constant to a particular antiderivative of the integrand, we obtain that ![]() .
.
Evaluate ![]()
Answer
![]()
Reduction Formulas
Evaluating ![]() for odd values of
for odd values of ![]() requires integration by parts. In addition, we must also know the value of
requires integration by parts. In addition, we must also know the value of ![]() to evaluate
to evaluate ![]() The evaluation of
The evaluation of ![]() also requires being able to integrate
also requires being able to integrate ![]() To make the process easier, we can derive and apply the following power reduction formulas. They allow us to replace the integral of a power of
To make the process easier, we can derive and apply the following power reduction formulas. They allow us to replace the integral of a power of ![]() or
or ![]() with the integral of a lower power of
with the integral of a lower power of ![]() or
or ![]()
Reduction Formulas for 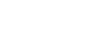 and
and 
![]()
![]()
The first power reduction rule may be verified by applying integration by parts. The second may be verified by rewriting ![]()
Revisiting 
Apply a reduction formula to evaluate ![]()
Solution
By applying the first reduction formula with ![]() , we obtain
, we obtain
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\ds {\int }^{}{\text{sec}}^{3}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill &\ds =\frac{1}{3-1}\text{sec}^{3-2}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)+\frac{3-2}{3-1}{\int }^{}\text{sec}^{3-2}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill \\[5mm]\ds \hfill &\ds =\frac{1}{2}\text{sec}\phantom{\rule{0.1em}{0ex}}(x)\phantom{\rule{0.1em}{0ex}}\text{tan}\phantom{\rule{0.1em}{0ex}}(x)+\frac{1}{2}\text{ln}|\text{sec}\phantom{\rule{0.1em}{0ex}}(x)+\text{tan}\phantom{\rule{0.1em}{0ex}}(x)|+C.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-a790e510fba8903ecc1b8efed64dbbd9_l3.png)
Using a Reduction Formula
Evaluate ![]()
Solution
Applying the second reduction formula with ![]() , we obtain
, we obtain
![]() .
.
To evaluate ![]() , we apply the second reduction formula with
, we apply the second reduction formula with ![]() , which allows to continue the chain of equalities as follows:
, which allows to continue the chain of equalities as follows:
![Rendered by QuickLaTeX.com \ds \begin{array}{cc}\hfill \ds{\int }^{}{\text{tan}}^{4}(x)\phantom{\rule{0.2em}{0ex}}\,dx &\ds =\frac{1}{3}{\text{tan}}^{3}(x)-{\int }^{}{\text{tan}}^{2}(x)\phantom{\rule{0.2em}{0ex}}\,dx \hfill \\[5mm]\ds &\ds =\frac{1}{3}{\text{tan}}^{3}(x)-\left(\frac1{2-1}\text{tan}^{2-1}\phantom{\rule{0.1em}{0ex}}(x)-{\int }^{}{\text{tan}}^{2-2}(x)\phantom{\rule{0.2em}{0ex}}\,dx \right)\hfill\\[5mm]\ds &\ds =\frac{1}{3}{\text{tan}}^{3}(x)-\text{tan}\phantom{\rule{0.1em}{0ex}}(x)+{\int }^{}1\phantom{\rule{0.2em}{0ex}}\,dx \hfill \\[5mm]\ds &\ds =\frac{1}{3}{\text{tan}}^{3}(x)-\text{tan}\phantom{\rule{0.1em}{0ex}}(x)+x+C.\hfill\end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7ba5226c12d0e86b19de8e1fe99ad0e1_l3.png)
Apply the reduction formula to ![]()
Answer
![]()
Key Concepts
Integrals of trigonometric functions can be evaluated using various strategies. These strategies include the following.
- Applying trigonometric identities to rewrite the integrand so that it may be evaluated via an apropriate substitution.
- Using integration by parts.
- Applying trigonometric identities to rewrite products of sines and cosines with different arguments as the sum of individual sine and cosine functions.
- Applying reduction formulas.
Key Equations
- Sine Products
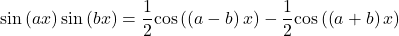
- Sine and Cosine Products
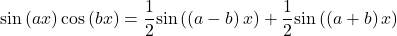
- Cosine Products
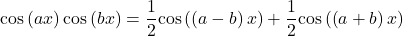
- Power Reduction Formula
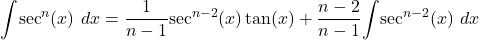
- Power Reduction Formula
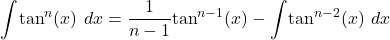
Exercises
Fill in the blank to make a true statement.
1. ![]()
Answer
![]()
2. ![]()
Use an identity to reduce the power of the trigonometric function to a trigonometric function raised to the first power.
3. ![]()
Answer
![]()
4. ![]()
Evaluate each of the following integrals using appropriate substitution.
5. ![]()
Answer
![]()
6. ![]()
7. ![]()
Answer
![]()
8. ![]()
9. ![]()
Answer
![]()
10. ![]()
Compute the following integrals using the guidelines for integrating powers of trigonometric functions. (Note: Some of the problems may be done using techniques of integration learned previously.)
11. ![]()
Answer
![]()
12. ![]()
13. ![]()
Answer
![]()
14. ![]()
15. ![]()
Answer
![]()
16. ![]()
17. ![]()
Answer
![]()
18. ![]()
19. ![]()
(Hint: use integration by parts)
Answer
![]()
20. ![]()
21. ![]()
Answer
![]()
22. ![]()
23. ![]()
Answer
![]()
24. ![]()
For the following exercises, evaluate the integrals involving parameter ![]() .
.
25. ![]()
Answer
![]()
26. ![]()
Use the double-angle formulas to evaluate the following integrals.
27. 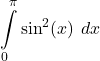
Answer
![]()
28. 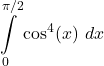
29. ![]()
Answer
![]()
30. ![]()
31. ![]()
Answer
![]()
32. ![]()
(Hint: to integrate ![]() , rewrite it as
, rewrite it as ![]() and use the formula.)
and use the formula.)
For the following exercises, evaluate the definite integrals using an appropriate trigonometric formula.
33. 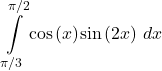
Answer
![]()
34. 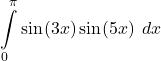
35. 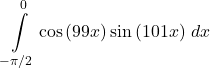
Answer
![]()
36. 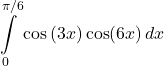
37. 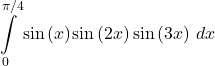
Answer
![]()
38. 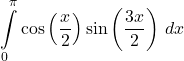
39. 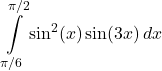
Answer
![]()
40. 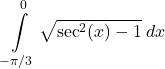
41. 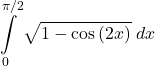
Answer
![]()
42. Find the area of the region bounded by the curves ![]()
43. Find the area of the region bounded by the curves ![]()
Answer
1
44. A particle moves in a straight line with the velocity function ![]() Find its position function
Find its position function ![]() if
if ![]()
45. Find the average value of the function ![]() over the interval
over the interval ![]()
Answer
![]()
46. Find the length of the curve ![]()
47. Find the length of the curve ![]()
Answer
![]()
48. Let ![]() be the region below the curve
be the region below the curve ![]() and above the x-axis over the interval
and above the x-axis over the interval ![]() . Find the volume generated by revolving
. Find the volume generated by revolving ![]() about the x-axis.
about the x-axis.
49. The inner product of two functions f and g over ![]() is defined by
is defined by 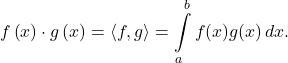 Two non-zero functions f and g are said to be orthogonal if
Two non-zero functions f and g are said to be orthogonal if ![]()
Show that ![]() and
and ![]() are orthogonal over the interval
are orthogonal over the interval ![]()
Answer
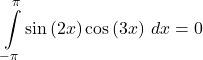
50. Let ![]() be real numbers such that
be real numbers such that ![]() . Evaluate
. Evaluate 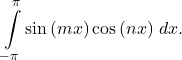
For each pair of integrals, determine which one is easier to evaluate. Explain your reasoning.
51. ![]() or
or ![]()
Answer
The first integral is easier to evaluate as it can be done just using a substitution evaluated ![]() , while the second integral is of a complicated type when the power of tangent is even and the power of secant is odd.
, while the second integral is of a complicated type when the power of tangent is even and the power of secant is odd.
52. ![]() or
or ![]()
Glossary
- power reduction formula
- a rule that allows an integral of a power of a trigonometric function to be exchanged for an integral involving a lower power
- trigonometric integral
- an integral involving powers and products of trigonometric functions

