0.1 Inverse Trigonometric Functions
Learning Objectives
-
Review the concept of an inverse function.
-
Define inverse trigonometric functions.
-
Learn how to simplify expressions involving both trigonometric and inverse trigonometric functions.
The inverse to a given function reverses the action of this function. In other words, the inverse function undoes whatever the function does. In this section, we recall the formal definition of an inverse function, state the necessary conditions for an inverse function to exist, and use this to define inverse trigonometric functions. We then discuss how to simlify expressions involving both trigonometric and inverse trigonometric functions.
Definition
Given a function ![]() with domain
with domain ![]() and range
and range ![]() , its inverse function (if it exists) is the function
, its inverse function (if it exists) is the function ![]() with domain
with domain ![]() and range
and range ![]() such that
such that
It follows that, for a function ![]() and its inverse
and its inverse ![]() ,
,
These are commonly referred to as cancellation equations .
Note that the -1 is not used as an exponent here, that is, ![]() .
.
The figure below shows the relationship between the domain and range of ![]() and the domain and range of
and the domain and range of ![]() .
.
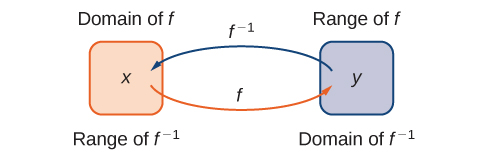
Recall that a function has exactly one output for each input. Therefore, to define an inverse function, we need to map each input to exactly one output. For example, let’s try to find the inverse function for ![]() . Solving the equation
. Solving the equation ![]() for
for ![]() we obtain
we obtain ![]() . This formula does not describe
. This formula does not describe ![]() as a function of
as a function of ![]() , because there are two values of
, because there are two values of ![]() corresponding to every
corresponding to every ![]() . So the problem with trying to find an inverse function for
. So the problem with trying to find an inverse function for ![]() is that two inputs can be sent to the same output. In contrast, there is no such issue with
is that two inputs can be sent to the same output. In contrast, there is no such issue with ![]() because, for this function, each input is sent to a different output. A function that sends each input to a different output is called a one-to-one function.
because, for this function, each input is sent to a different output. A function that sends each input to a different output is called a one-to-one function.
Definition
We say that ![]() is a one-to-one function if
is a one-to-one function if ![]() whenever
whenever ![]() .
.
One way to determine whether a function is one-to-one is by looking at its graph. If a function is one-to-one, then no two inputs can be sent to the same output. Therefore, if we draw a horizontal line anywhere in the ![]() -plane it cannot intersect the graph more than once. This establishes the horizontal line test to determine whether a function is one-to-one.
-plane it cannot intersect the graph more than once. This establishes the horizontal line test to determine whether a function is one-to-one.
Horizontal Line Test
A function ![]() is one-to-one if and only if every horizontal line intersects the graph of
is one-to-one if and only if every horizontal line intersects the graph of ![]() no more than once.
no more than once.
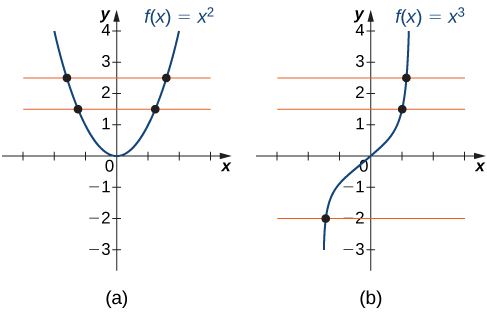
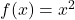 is not one-to one as it doesn’t pass the horizontal line test. (b) The function
is not one-to one as it doesn’t pass the horizontal line test. (b) The function 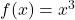 is one-to-one.
is one-to-one.Do not confuse the horizontal line test with the vertical line test that determines whether a given curve is the graph of a function.
Determining Whether a Function Is One-to-One
For each of the following functions, use the horizontal line test to determine whether it is one-to-one.
Solution
-
Since the horizontal line
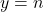 for any integer
for any integer 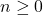 intersects the graph more than once, this function is not one-to-one. (The function represented by this graph is called the floor function, it is denoted by
intersects the graph more than once, this function is not one-to-one. (The function represented by this graph is called the floor function, it is denoted by  , and
, and 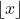 is equal to the biggest integer that does not exceed
is equal to the biggest integer that does not exceed 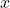 .)
.)

-
Since every horizontal line intersects the graph at most once, this function is one-to-one.

Is the function ![]() graphed in the following image one-to-one?
graphed in the following image one-to-one?
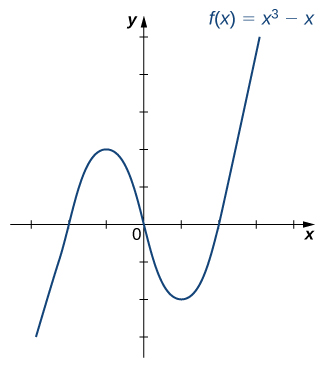
Answer
No.
Graphing Inverse Functions
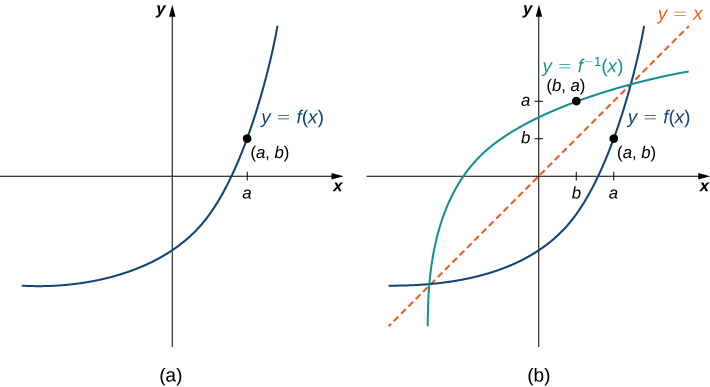
We now discuss the relationship between the graph of a function ![]() and the graph of its inverse. Consider the graph of
and the graph of its inverse. Consider the graph of ![]() shown below and a point
shown below and a point ![]() on the graph. Since
on the graph. Since ![]() , we have that
, we have that ![]() . Therefore, when we graph
. Therefore, when we graph ![]() , the point
, the point ![]() is on the graph. As a result, the graph of
is on the graph. As a result, the graph of ![]() is a reflection of the graph of
is a reflection of the graph of ![]() about the line
about the line ![]() .
.
 is symmetric to the graph of
is symmetric to the graph of  with respect to the line
with respect to the line 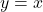 .
.Sketching Graphs of Inverse Functions
For the graph of ![]() in the following image, sketch a graph of
in the following image, sketch a graph of ![]() by sketching the line
by sketching the line ![]() and using symmetry. Identify the domain and range of
and using symmetry. Identify the domain and range of ![]() .
.
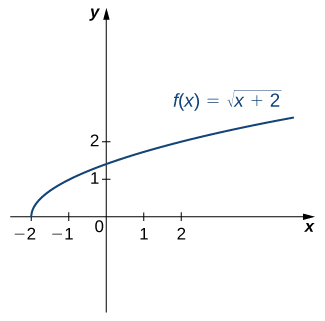
Solution
Reflect the graph about the line ![]() . The domain of
. The domain of ![]() coincides with the range of
coincides with the range of ![]() , which is
, which is ![]() , and the range of
, and the range of ![]() coincides with the domain of
coincides with the domain of ![]() , which is
, which is ![]() . In fact,
. In fact, ![]() ,
, ![]() , that can be verified by solving
, that can be verified by solving ![]() for
for ![]() and interchanging the variables
and interchanging the variables ![]() and
and ![]() in the formula obtained.
in the formula obtained.

Sketch the graph of ![]() and the graph of its inverse using the symmetry property of inverse functions.
and the graph of its inverse using the symmetry property of inverse functions.
Answer

Restricted Domains
As we have seen, ![]() does not have an inverse function because it is not one-to-one. However, we can choose a subset of the domain of
does not have an inverse function because it is not one-to-one. However, we can choose a subset of the domain of ![]() such that the function still has the same range over this subset and is one-to-one on it. Such subset is called a restricted domain. By restricting the domain of
such that the function still has the same range over this subset and is one-to-one on it. Such subset is called a restricted domain. By restricting the domain of ![]() , we can define a new function
, we can define a new function ![]() such that the domain of
such that the domain of ![]() is the restricted domain of
is the restricted domain of ![]() and
and ![]() for all
for all ![]() in the domain of
in the domain of ![]() . Then we can define an inverse function for
. Then we can define an inverse function for ![]() on that domain. For example, since
on that domain. For example, since ![]() is one-to-one on the interval
is one-to-one on the interval ![]() and the function
and the function ![]() still takes all non-negative values (which is the range of
still takes all non-negative values (which is the range of ![]() ) when
) when ![]() changes in this interval, we can define a new function
changes in this interval, we can define a new function ![]() such that the domain of
such that the domain of ![]() is
is ![]() and
and ![]() for all
for all ![]() in its domain. Since
in its domain. Since ![]() is a one-to-one function, it has an inverse function, given by the formula
is a one-to-one function, it has an inverse function, given by the formula ![]() . On the other hand, the function
. On the other hand, the function ![]() is also one-to-one and takes all non-negative values on the domain
is also one-to-one and takes all non-negative values on the domain ![]() . Therefore, we could also define a new function
. Therefore, we could also define a new function ![]() such that the domain of
such that the domain of ![]() is
is ![]() and
and ![]() for all
for all ![]() in the domain of
in the domain of ![]() . Then
. Then ![]() is a one-to-one function and must also have an inverse. Its inverse is given by the formula
is a one-to-one function and must also have an inverse. Its inverse is given by the formula ![]() .
.
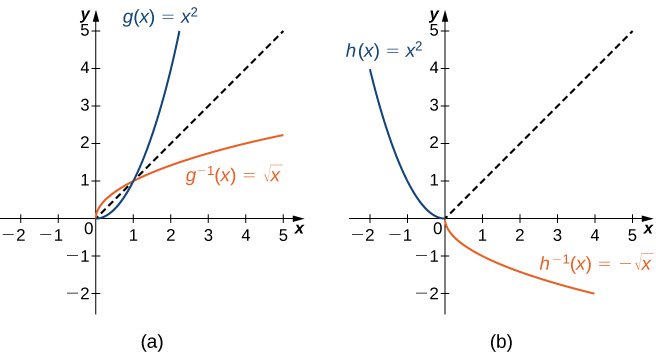
 , where
, where 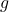 is the restriction of
is the restriction of 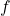 to
to 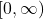 .
.(b)
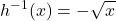 , where
, where 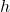 is the restriction of
is the restriction of 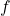 to
to ![Rendered by QuickLaTeX.com (-\infty,0]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-caa2115449743605b9b071096189defb_l3.png) .
.Inverse Trigonometric Functions
The six basic trigonometric functions are periodic, and therefore they are not one-to-one. However, if we restrict the domain of a trigonometric function to an interval where it is one-to-one, we can define its inverse. Let us start with the sine function. The sine function is one-to-one and takes all values from its range ![]() on an infinite number of intervals, but the standard convention is to restrict the domain to the interval
on an infinite number of intervals, but the standard convention is to restrict the domain to the interval ![]() . By doing so, we define the inverse sine function on the domain
. By doing so, we define the inverse sine function on the domain ![]() such that for any
such that for any ![]() in the interval
in the interval ![]() , the inverse sine function tells us which angle
, the inverse sine function tells us which angle ![]() in the interval
in the interval ![]() satisfies
satisfies ![]() . Similarly, we can restrict the domains of the other trigonometric functions to define inverse trigonometric functions, which are functions that tell us which angle in a certain interval has a specified trigonometric value.
. Similarly, we can restrict the domains of the other trigonometric functions to define inverse trigonometric functions, which are functions that tell us which angle in a certain interval has a specified trigonometric value.
Definition
The inverse sine function, denoted ![]() or
or ![]() , and the inverse cosine function, denoted
, and the inverse cosine function, denoted ![]() or
or ![]() are defined on the domain
are defined on the domain ![]() as follows:
as follows:
![Rendered by QuickLaTeX.com \begin{array}{c}\sin^{-1}(x)=y \,\, \text{if and only if} \, \sin (y)=x \, \text{and} \, -\displaystyle\frac{\pi}{2} \le y \le \frac{\pi}{2};\hfill \\[3mm] \cos^{-1}(x)=y \,\, \text{if and only if} \, \cos (y)=x \, \text{and} \, 0 \le y \le \pi. \hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-7232c38bac64b92d253ca36e48c2fa28_l3.png)
The inverse tangent function, denoted ![]() or
or ![]() , and inverse cotangent function, denoted
, and inverse cotangent function, denoted ![]() or
or ![]() , are defined on the domain
, are defined on the domain ![]() as follows:
as follows:
![Rendered by QuickLaTeX.com \begin{array}{c}\tan^{-1}(x)=y \,\, \text{if and only if} \, \tan (y)=x \, \text{and} \, \displaystyle-\frac{\pi}{2}<y<\frac{\pi}{2};\hfill \\[3mm] \cot^{-1}(x)=y \,\, \text{if and only if} \, \cot (y)=x \, \text{and} \, 0<y<\pi. \hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-2cfa702604aaed65fffd19e8c58544e7_l3.png)
The inverse cosecant function, denoted ![]() or
or ![]() , and inverse secant function, denoted
, and inverse secant function, denoted ![]() or
or ![]() , are defined on the domain
, are defined on the domain ![]() as follows:
as follows:
![Rendered by QuickLaTeX.com \begin{array}{c}\csc^{-1}(x)=y \,\, \text{if and only if} \, \csc (y)=x \, \text{and} \, \displaystyle-\frac{\pi}{2} \le y \le \frac{\pi}{2}, \, y\ne 0;\hfill \\[3mm] \sec^{-1}(x)=y \,\, \text{if and only if} \, \sec (y)=x \, \text{and} \, 0 \le y \le \pi, \, y \ne \frac{\pi}2.\hfill \end{array}](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-4edb0c42e227460a71431235ed3756e8_l3.png)
Finding Domains of Functions Involving Inverse Trigonometric Functions
Determine the domain of the function ![]() .
.
Solution
Since the domain of inverse sine is ![]() , we have that
, we have that ![]() must satisfy
must satisfy ![]() . We solve each of the inequalities separately.
. We solve each of the inequalities separately.
![]()
Zeroes of the right hand side are -2 and -1, and they divide the ![]() -axis into subintervals
-axis into subintervals ![]() ,
, ![]() , and
, and ![]() . Using sample points or any other appropriate method, we determine that the inequality is satisfied for
. Using sample points or any other appropriate method, we determine that the inequality is satisfied for ![]() , where the endpoints of the intervals are included since the inequality is not strict. Likewise,
, where the endpoints of the intervals are included since the inequality is not strict. Likewise,
![]() .
.
Since ![]() must satisfy both inequalities, our domain is going to be the intersection of
must satisfy both inequalities, our domain is going to be the intersection of ![]() and
and ![]() , which is
, which is ![]() .
.
Find the domain of the function ![]() .
.
Answer
![]()
To graph the inverse trigonometric functions, we use the graphs of the trigonometric functions restricted to the domains specified earlier and reflect the graphs about the line ![]() to obtain the curves shown below.
to obtain the curves shown below.

When evaluating an inverse trigonometric function, the output is an angle. For example, to evaluate ![]() , we need to find an angle
, we need to find an angle ![]() such that
such that ![]() . Clearly, many angles have this property. However, given the definition of
. Clearly, many angles have this property. However, given the definition of ![]() , we need the angle
, we need the angle ![]() that not only solves this equation, but also lies in the interval
that not only solves this equation, but also lies in the interval ![]() We conclude that
We conclude that ![]() .
.
We now consider a composition of a trigonometric function and its inverse. For example, consider the two expressions 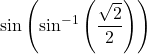 and
and ![]() . For the first one, we simplify as follows:
. For the first one, we simplify as follows: 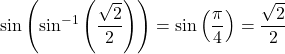 .
.
For the second one, we have ![]() .
.
The inverse function is supposed to “undo” the original function, so why isn’t ![]() ? Recalling our definition of inverse functions, a function
? Recalling our definition of inverse functions, a function ![]() and its inverse
and its inverse ![]() satisfy the conditions
satisfy the conditions ![]() for all
for all ![]() in the domain of
in the domain of ![]() and
and ![]() for all
for all ![]() in the domain of
in the domain of ![]() , so what happened here? The issue is that the inverse sine function,
, so what happened here? The issue is that the inverse sine function, ![]() is the inverse of the restricted sine function defined on the domain
is the inverse of the restricted sine function defined on the domain ![]() . Therefore, for
. Therefore, for ![]() in the interval
in the interval ![]() , it is true that
, it is true that ![]() . However, for values of
. However, for values of ![]() outside this interval, the equation does not hold, even though
outside this interval, the equation does not hold, even though ![]() is defined for all real numbers
is defined for all real numbers ![]() .
.
What about ![]() ? Does that have a similar issue? The answer is no . Since the domain of
? Does that have a similar issue? The answer is no . Since the domain of ![]() is the interval
is the interval ![]() , we conclude that
, we conclude that ![]() if
if ![]() and the expression is not defined for other values of
and the expression is not defined for other values of ![]() . To summarize,
. To summarize,
Likewise, for the cosine function, ![]() and
and ![]() .
.
Similar properties hold for the other trigonometric functions and their inverses.
Evaluating Expressions Involving Inverse Trigonometric Functions
Evaluate each of the following expressions.
Solution
-
Evaluating
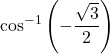 is equivalent to finding the angle
is equivalent to finding the angle 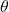 such that
such that 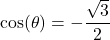 and
and 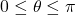 . Using the unit circle, we see that the angle
. Using the unit circle, we see that the angle 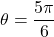 satisfies these two conditions. Therefore,
satisfies these two conditions. Therefore, 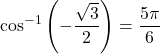 .
. -
Since
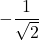 is not equal to a cotangent of a standard angle, we cannot evaluate
is not equal to a cotangent of a standard angle, we cannot evaluate 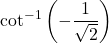 without a calculator. However, since the functions
without a calculator. However, since the functions 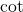 and
and 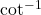 are mutually inverse and
are mutually inverse and 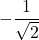 is in the domain of
is in the domain of 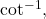 which is
which is 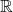 , we conclude that
, we conclude that 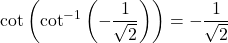 .
. -
Let
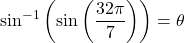 . Then the angle
. Then the angle 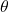 we are looking for should satisfy
we are looking for should satisfy 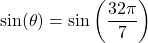 and
and 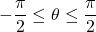 . We have that
. We have that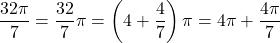 .
.Since sine function is
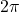 -periodic,
-periodic, 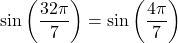 . However,
. However, 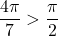 , which means that
, which means that 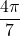 does not belong to the interval
does not belong to the interval ![Rendered by QuickLaTeX.com \ds\left[-\frac{\pi}2,\frac{\pi}2\right]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-896ed511a5900231a9846563e4ab9c24_l3.png) , and hence it is not our answer yet. To “bring” the angle into the desired interval, we can use either the unit circle or the properties of the sine function, in this case,
, and hence it is not our answer yet. To “bring” the angle into the desired interval, we can use either the unit circle or the properties of the sine function, in this case, 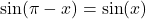 . We have
. We have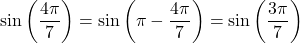 , and hence,
, and hence, 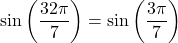 . Because
. Because ![Rendered by QuickLaTeX.com \ds\frac{3\pi}{7}\in\left[-\frac{\pi}2,\frac{\pi}2\right]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-fe69b9a5aa51f775fa3b1c58f033953b_l3.png) , we obtain that
, we obtain that 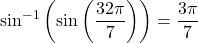 .
. -
Let
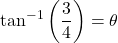 . Then
. Then 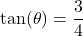 ,
, 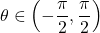 , and we need to find
, and we need to find 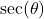 . Note that since
. Note that since 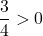 , we can even say that
, we can even say that 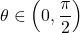 . We can solve this question either using right triangle trigonometry, or applying an appropriate trigonometric formula. With the geometric approach, we draw a right triangle with acute angle
. We can solve this question either using right triangle trigonometry, or applying an appropriate trigonometric formula. With the geometric approach, we draw a right triangle with acute angle 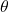 , opposite side 3 and adjacent side 4, as
, opposite side 3 and adjacent side 4, as 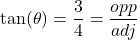 . Then, by the Pythagorean theorem, the hypotenuse has length
. Then, by the Pythagorean theorem, the hypotenuse has length 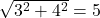 . It follows that
. It follows that 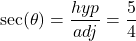 . Alternatively, we can use the formula
. Alternatively, we can use the formula 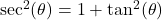 (that follows from the Pythagorean trigonometric identity
(that follows from the Pythagorean trigonometric identity 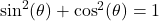 by expressing
by expressing  and
and 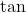 in terms of
in terms of 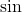 and
and 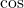 and bringing the right hand side to the common denominator). Since secant is positive on the interval
and bringing the right hand side to the common denominator). Since secant is positive on the interval 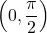 , we obtain that
, we obtain that 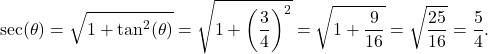
-
Note that since
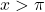 , we have that
, we have that 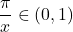 , and so
, and so 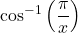 is well-defined. If
is well-defined. If 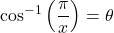 , then
, then ![Rendered by QuickLaTeX.com \theta\in[0,\pi]](https://pressbooks.openedmb.ca/app/uploads/quicklatex/quicklatex.com-542a93dc074eff86df24854463f32075_l3.png) , and we are looking for
, and we are looking for 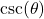 . Because
. Because 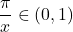 , we have that
, we have that 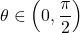 , and hence
, and hence 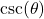 is well-defined. Using a triangle diagram (
is well-defined. Using a triangle diagram (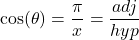 , so we take adjacent side to be
, so we take adjacent side to be 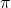 , hypotenuse to be
, hypotenuse to be 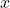 , and then, applying the Pythagoren theorem, we obtain that the opposite side is going to be
, and then, applying the Pythagoren theorem, we obtain that the opposite side is going to be 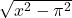 ), we find that
), we find that 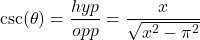 . Alternatively,
. Alternatively, 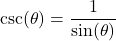 and
and 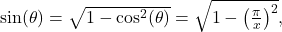 which follows from the Pythagorean trigonometric identity
which follows from the Pythagorean trigonometric identity 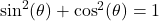 since
since 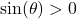 on
on 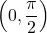 , implying that
, implying that 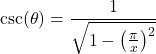 . It is an easy, yet useful, exercise to verify that the two answers we obtained are actually the same.
. It is an easy, yet useful, exercise to verify that the two answers we obtained are actually the same.
Key Concepts and Equations
-
For a function to have an inverse, the function must be one-to-one. Given the graph of a function, we can determine whether the function is one-to-one by using the horizontal line test.
-
If a function is not one-to-one, we can restrict the domain to a smaller domain where the function is one-to-one and then define the inverse of the function on the smaller domain.
-
For a function
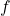 and its inverse
and its inverse 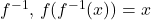 for all
for all 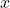 in the domain of
in the domain of 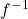 and
and 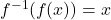 for all
for all 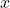 in the domain of
in the domain of 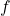 .
. -
Since the trigonometric functions are periodic, we need to restrict their domains to define the inverse trigonometric functions.
-
The graph of a function
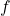 and its inverse
and its inverse 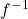 are symmetric about the line
are symmetric about the line 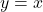 .
.
Exercises
For the following exercises, find the domains of the given functions.
1. ![]()
Answer
![]()
2. ![]()
3. ![]()
Answer
![]()
4. ![]()
For the following exercises, evaluate the functions, when possible. If the function is undefined, explain why.
5. 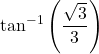
Answer
![]()
6. 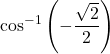
7. ![]()
Answer
![]()
8. ![]()
9. ![]()
Answer
![]()
10. ![]()
11. ![]()
Answer
Undefined
13. ![]()
Answer
![]()
14. ![]()
15. ![]()
Answer
![]()
16. ![]()
Glossary
- inverse function
- for a function
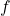 , the inverse function
, the inverse function 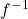 is defined if
is defined if 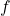 is one-to-one by
is one-to-one by 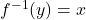 whenever
whenever 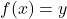
- one-to-one function
- a function
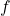 is one-to-one if
is one-to-one if 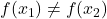 whenever
whenever 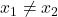
- horizontal line test
- a function
 is one-to-one if and only if every horizontal line intersects the graph of
is one-to-one if and only if every horizontal line intersects the graph of  at most once
at most once
- restricted domain
- a subset of the domain of a function
- inverse trigonometric functions
- the inverses of the trigonometric functions are defined on restricted domains where they are one-to-one functions

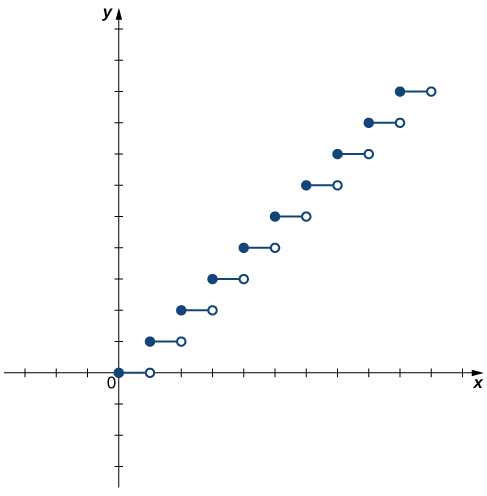
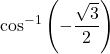

Hint
Use the horizontal line test.