True or False ? Justify your answer with a proof or a counterexample.
1. A function is always one-to-one.
2. [latex]f \circ g=g\circ f[/latex], assuming [latex]f[/latex] and [latex]g[/latex] are functions.
Solution
False
3. A relation that passes the horizontal and vertical line tests is a one-to-one function.
4. A relation passing the horizontal line test is a function.
Solution
False
For the following problems, state the domain and range of the given functions:
[latex]f=x^2+2x-3,\phantom{\rule{3em}{0ex}}g=\ln(x-5),\phantom{\rule{3em}{0ex}}h=\frac{1}{x+4}[/latex]
5. [latex]h[/latex]
6. [latex]g[/latex]
Solution
Domain: [latex](5,\infty)[/latex], Range: all real numbers
7. [latex]h\circ f[/latex]
8. [latex]g\circ f[/latex]
Solution
Domain: [latex](-\infty,-4) \cup (2,\infty)[/latex], Range: all real numbers
Given the following functions, determine: [latex]f(2), f(a)[/latex] and [latex]f(a+h)[/latex]
9. [latex]f(x)=\frac{5}{2x-3}[/latex]
10. [latex]f(x)=\frac{x}{x-1}[/latex]
Solution
[latex]f(2) = 2, f(a) = \frac{a}{a-1}, f(a+h) = \frac{a+h}{a+h-1}[/latex]
11. [latex]f(x)=\sqrt{7-x}[/latex]
12. [latex]f(x)=\frac{x^2-1}{x-2}[/latex]
Solution
[latex]f(2)[/latex] does not exist since 2 is not in the domain of [latex]f[/latex], [latex]f(a) = \frac{a^2-1}{a-2}, f(a+h) = \frac{(a+h)^2-1}{a+h-2} = \frac{a^2 + 2ah + h^2 -1}{a+h-2}[/latex]
Determine the domain of each function. Write your answer in interval notation.
13. [latex]f(x)=\frac{x+5}{\sqrt{x^2+5x-14}}[/latex]
14. [latex]f(x)=\frac{x-2}{\sqrt{x^2-3x+2}}[/latex]
Solution
Domain: [latex](-\infty,1) \cup (2,\infty)[/latex]
15. [latex]f(x)=\sqrt{5x-1} - \sqrt{x}[/latex]
16. [latex]f(x)=\sqrt{3x} - \sqrt{2-x}[/latex]
Solution
Domain: [latex][0,2][/latex]
17. [latex]f(x)=\frac{x^2+3}{\sqrt{x^2-9}}[/latex]
18. [latex]f(x)=\frac{x^2+3}{\sqrt{9-x^2}}[/latex]
Solution
Domain: [latex](-3,3)[/latex]
19. [latex]f(x)=e^{x^2+x-2}[/latex]
20. [latex]f(x)= \frac{x}{1-e^{3x^2-4x-7}}[/latex]
Solution
Domain: [latex](-\infty,-1) \cup (-1, \frac{7}{3}) \cup (\frac{7}{3},\infty)[/latex]
21. [latex]f(x)= \ln(16-x^2)[/latex]
22. [latex]f(x)= \ln(2x^2-50)[/latex]
Solution
Domain: [latex](-\infty,-5) \cup (5,\infty)[/latex]
23. [latex]f(x)= \frac{4x}{|x^2-36|}[/latex]
24. [latex]f(x)= \frac{\sqrt{x-7}}{|x^2-49|}[/latex]
Solution
Domain: [latex](7,\infty)[/latex]
25. [latex]f(x)= \frac{\sqrt{9-x}}{x^2-5x-24}[/latex]
26. [latex]f(x)= \frac{\sqrt{x^2-6x+8}}{16-x^2}[/latex]
Solution
Domain: [latex](-\infty,-4) \cup (-4,2] \cup (4,\infty)[/latex]
27. [latex]g(x) =\frac{\sqrt{4-x}}{x^2+3x+2}[/latex]
28. [latex]h(x)=\dfrac{\sqrt{1-e^x}}{x+6}[/latex]
Solution
Domain: [latex](-\infty,-6)\cup(-6,0][/latex]
Find the inverse of the following functions.
29. [latex]f(x)=\frac{2x-1}{7}[/latex]
30. [latex]g(x)=\frac{x-8}{2x+1}[/latex]
Solution
[latex]g^{-1}(x)= \frac{-x-8}{2x-1}[/latex]
31. [latex]g(x)=\ln(x-7)[/latex]
32. [latex]f(x)=e^{2x}-3[/latex]
Solution
[latex]f^{-1}(x)= \frac{lnx+3}{2}[/latex]
Find the degree, [latex]y[/latex]-intercept, and zeros for the following polynomial functions.
33. [latex]f(x)=2x^2+9x-5[/latex]
34. [latex]f(x)=x^3+2x^2-2x[/latex]
Solution
Degree of 3, [latex]y[/latex]-intercept: 0, Zeros: 0, [latex]\sqrt{3}-1, \, -1-\sqrt{3}[/latex]
Simplify the following trigonometric expressions.
35. [latex]\frac{\tan^2 x}{\sec^2 x}+\cos^2 x[/latex]
36. [latex]\cos(2x)=\sin^2 x[/latex]
Solution
[latex]\cos(2x)[/latex] or [latex]\frac{1}{2}(\cos(2x)+1)[/latex]
Solve the following trigonometric equations on the interval [latex]\theta =[-2\pi ,2\pi][/latex] exactly.
37. [latex]6\cos^2 x-3=0[/latex]
38. [latex]\sec^2 x-2\sec x+1=0[/latex]
Solution
[latex]0, \, \pm 2\pi[/latex]
Solve the following logarithmic equations.
39. [latex]5^x=16[/latex]
40. [latex]\log_2 (x+4)=3[/latex]
Solution
4
Are the following functions one-to-one over their domain of existence? Does the function have an inverse? If so, find the inverse [latex]f^{-1}(x)[/latex] of the function. Justify your answer.
41. [latex]f(x)=x^2+2x+1[/latex]
42. [latex]f(x)=\frac{1}{x}[/latex]
Solution
One-to-one; yes, the function has an inverse; inverse: [latex]f^{-1}(x)=\frac{1}{x}[/latex]
For the following problems, determine the largest domain on which the function is one-to-one and find the inverse on that domain.
43. [latex]f(x)=\sqrt{9-x}[/latex]
44. [latex]f(x)=x^2+3x+4[/latex]
Solution
[latex]x \ge -\frac{3}{2}, \, f^{-1}(x)=-\frac{3}{2}+\frac{1}{2}\sqrt{4y-7}[/latex]
Sketch the following piece-wise functions.
45. [latex]f(x)=\begin{cases} x+7, & x < 1 \\ x-5 & x \ge 1 \end{cases}[/latex]
46. [latex]f(x)=\begin{cases} x^2-1, & x < -2 \\ x+2 & x \ge -2 \end{cases}[/latex]
Solution
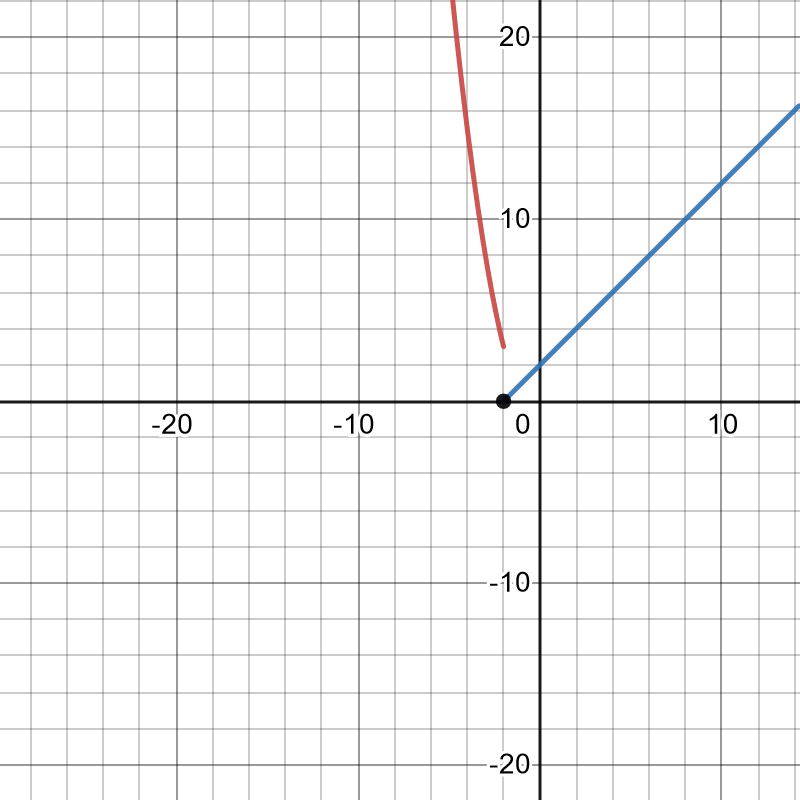
47. [latex]f(x)=\begin{cases} x-1, & x < 1 \\ 4, & x=1 \\ \sqrt{x+2} & x > 1 \end{cases}[/latex]
48. [latex]f(x)=\begin{cases} x^2, & x < -1 \\ x-7, & x=-1 \\ \sqrt{x+3} & x > -1 \end{cases}[/latex]
Solution
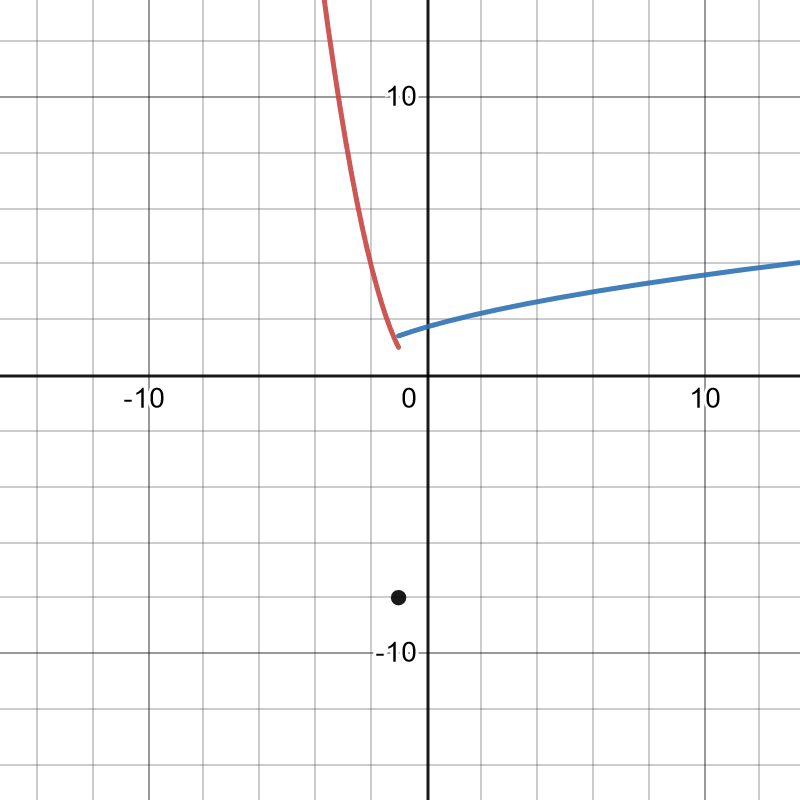
Write the following absolute value functions as piece-wise functions and sketch.
49. [latex]f(x)=|2x-5|[/latex]
50. [latex]f(x)=|3x+7|[/latex]
Solution
[latex]f(x)=\begin{cases} -(3x+7), & x < -\frac{7}{3} \\ 3x+7 & x \ge -\frac{7}{3} \end{cases}[/latex] 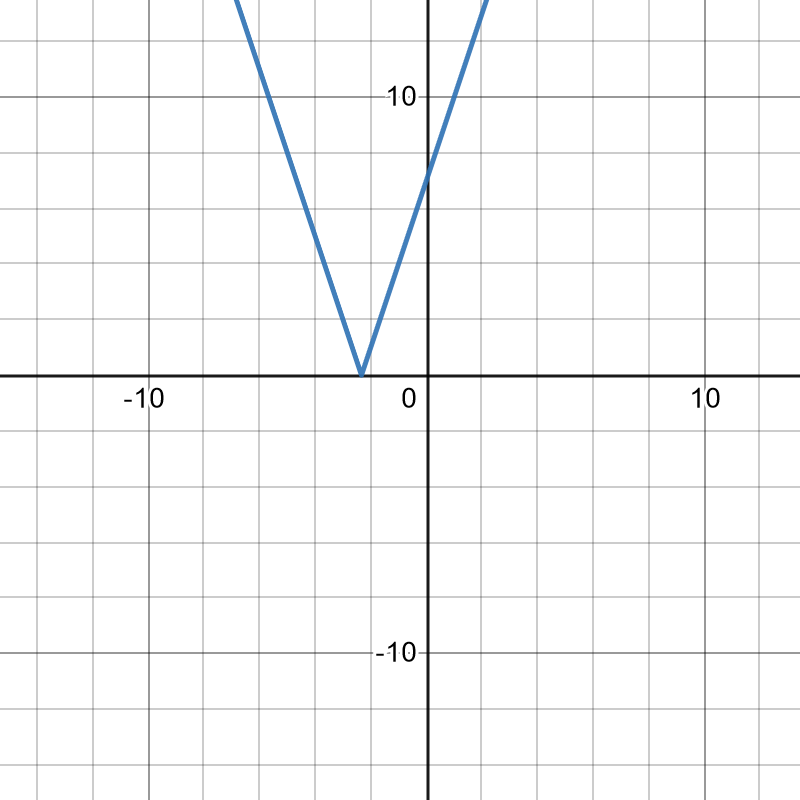
Answer the following question.
51. A car is racing along a circular track with diameter of 1 mi. A trainer standing in the center of the circle marks his progress every 5 sec. After 5 sec, the trainer has to turn [latex]55^{\circ}[/latex] to keep up with the car. How fast is the car traveling?
For the following problems, consider a restaurant owner who wants to sell T-shirts advertising his brand. He recalls that there is a fixed cost and variable cost, although he does not remember the values. He does know that the T-shirt printing company charges $440 for 20 shirts and $1000 for 100 shirts.
52. a. Find the equation [latex]C=f(x)[/latex] that describes the total cost as a function of number of shirts and b. determine how many shirts he must sell to break even if he sells the shirts for $10 each.
Solution
a. [latex]C(x)=300+7x[/latex] b. 100 shirts
53. a. Find the inverse function [latex]x=f^{-1}(C)[/latex] and describe the meaning of this function. b. Determine how many shirts the owner can buy if he has $8000 to spend.
For the following problems, consider the population of Ocean City, New Jersey, which is cyclical by season.
54. The population can be modeled by [latex]P(t)=82.5-67.5\cos [(\pi /6)t][/latex], where [latex]t[/latex] is time in months ([latex]t=0[/latex] represents January 1) and [latex]P[/latex] is population (in thousands). During a year, in what intervals is the population less than 20,000? During what intervals is the population more than 140,000?
Solution
The population is less than 20,000 from December 8 through January 23 and more than 140,000 from May 29 through August 2
55. In reality, the overall population is most likely increasing or decreasing throughout each year. Let’s reformulate the model as [latex]P(t)=82.5-67.5\cos [(\pi /6)t]+t[/latex], where [latex]t[/latex] is time in months ([latex]t=0[/latex] represents January 1) and [latex]P[/latex] is population (in thousands). When is the first time the population reaches 200,000?
For the following problems, consider radioactive dating. A human skeleton is found in an archeological dig. Carbon dating is implemented to determine how old the skeleton is by using the equation [latex]y=e^{rt}[/latex], where [latex]y[/latex] is the percentage of radiocarbon still present in the material, [latex]t[/latex] is the number of years passed, and [latex]r=-0.0001210[/latex] is the decay rate of radiocarbon.
56. If the skeleton is expected to be 2000 years old, what percentage of radiocarbon should be present?
Solution
78.51%
57. Find the inverse of the carbon-dating equation. What does it mean? If there is 25% radiocarbon, how old is the skeleton?

