True or False ? Justify your answer with a proof or a counterexample. Assume that [latex]f(x)[/latex] is continuous and differentiable unless stated otherwise.

1.  If [latex]f(-1)=-6[/latex] and [latex]f(1)=2,[/latex] then there exists at least one point [latex]x\in \left[-1,1\right][/latex] such that [latex]{f}^{\prime }(x)=4.[/latex]

Solution

True, by Mean Value Theorem

2.  If [latex]{f}^{\prime }(c)=0,[/latex] there is a maximum or minimum at [latex]x=c.[/latex]

3.  There is a function such that [latex]f(x) < 0,{f}^{\prime }(x) < 0,[/latex] and [latex]f''(x) < 0.[/latex] (A graphical “proof” is acceptable for this answer.)

Solution

True

4.  There is a function such that there is both an inflection point and a critical number for some value [latex]x=a.[/latex]

Answer the following questions.

5.  Given the graph of [latex]{f}^{\prime },[/latex] determine where [latex]f[/latex] is increasing or decreasing.

The function increases to cross the x-axis at -2, reaches a maximum and then decreases through the origin, reaches a minimum and then increases to a maximum at 2, decreases to a minimum and then increases to pass through the x-axis at 4 and continues increasing.

Solution

Increasing: [latex](-2,0)\cup (4,\infty ),[/latex] decreasing: [latex](-\infty ,-2)\cup (0,4)[/latex]

6.  The graph of [latex]f[/latex] is given below. Draw [latex]{f}^{\prime }.[/latex]

The function decreases rapidly and reaches a local minimum at -2, then it increases to reach a local maximum at 0, at which point it decreases slowly at first, then stops decreasing near 1, then continues decreasing to reach a minimum at 3, and then increases rapidly.

7.  Find the linear approximation [latex]L(x)[/latex] to [latex]y={x}^{2}+ \tan (\pi x)[/latex] near [latex]x=\frac{1}{4}.[/latex]

Solution

[latex]L(x)=\frac{17}{16}+\frac{1}{2}(1+4\pi )(x-\frac{1}{4})[/latex]

8.  Find the differential of [latex]y={x}^{2}-5x-6[/latex] and evaluate for [latex]x=2[/latex] with [latex]dx=0.1.[/latex]

Find the critical numbers and the local and absolute extrema of the following functions on the given interval.

9.  [latex]f(x)=x+{ \sin }^{2}(x)[/latex] over [latex]\left[0,\pi \right][/latex]

Solution

Critical number: [latex]x=\frac{3\pi }{4},[/latex] absolute minimum: [latex]y=0,[/latex] absolute maximum: [latex]y=\pi[/latex]

10.  [latex]f(x)=3{x}^{4}-4{x}^{3}-12{x}^{2}+6[/latex] over [latex]\left[-3,3\right][/latex]

Determine over which intervals the following functions are increasing, decreasing, concave up, and concave down.

11.  [latex]x(t)=3{t}^{4}-8{t}^{3}-18{t}^{2}[/latex]

Solution

Increasing: [latex](-1,0)\cup (3,\infty ),[/latex] decreasing: [latex](-\infty ,-1)\cup (0,3),[/latex] concave up: [latex](-\infty ,\frac{1}{3}(2-\sqrt{13}))\cup (\frac{1}{3}(2+\sqrt{13}),\infty ),[/latex] concave down: [latex](\frac{1}{3}(2-\sqrt{13}),\frac{1}{3}(2+\sqrt{13}))[/latex]

12.  [latex]y=x+ \sin (\pi x)[/latex]

13.  [latex]g(x)=x-\sqrt{x}[/latex]

Solution

Increasing: [latex](\frac{1}{4},\infty ),[/latex] decreasing: [latex](0,\frac{1}{4}),[/latex] concave up: [latex](0,\infty ),[/latex] concave down: nowhere

14.  [latex]f(\theta )= \sin (3\theta )[/latex]

Use L’Hopital’s Rule to determine the following limits.

15.  [latex]\underset{x\to 1}{\text{lim}}\frac{x-1}{ \sin (\pi x)}[/latex]

Solution

[latex]-\frac{1}{\pi }[/latex]

16.  [latex]\underset{x\to \infty }{\text{lim}}{(3x)}^{1\text{/}x}[/latex]

Use Newton’s method to find the first two iterations, given the starting point.

17.  [latex]y={x}^{3}+1,{x}_{0}=0.5[/latex]

Solution

[latex]{x}_{1}=-1,{x}_{2}=-1[/latex]

18.  [latex]\frac{1}{x+1}=\frac{1}{2},{x}_{0}=0[/latex]

Find the antiderivative of each function.

19.  [latex]g(x)=\sqrt{x}-\frac{1}{{x}^{2}}[/latex]

Solution

[latex]G(x)=\frac{2{x}^{3\text{/}2}}{3}+\frac{1}{x}+C[/latex]

20. [latex]f(x)=4x^{\frac{3}{5}} - \sin x + e^{2x}[/latex]

21. [latex]f(x)= \frac{5}{\sqrt{x^3}} + \pi ^2 - \frac{1}{x}[/latex]

Solution

[latex]F(x)=\frac{-10}{\sqrt{x}}+\pi ^2 x - \ln |x| +C[/latex]

22. [latex]f(x)=\sec ^2 x + \sin x - e^{-4x}[/latex]

Evaluate the indefinite integral.

23. [latex]\int (3x^2 + \frac{7}{x}) dx[/latex]

Solution

[latex]x^3 + 7 \ln |x|+C[/latex]

24. [latex]\int (\frac{5x^6 + \sqrt{x^5}}{\sqrt{x}}) dx[/latex]

25. [latex]\int ((2x^2+1)(x-3) + \sin x) dx[/latex]

Solution

[latex]\frac{x^4}{2} - 2 x^3 + \frac{x^2}{2} - 3x - \cos x + C[/latex]

26. [latex]\int (\sec ^2 x-e^{-6x} ) dx[/latex]

Solve the initial value problems.

27. Given a particle is moving with the data below, find the position of the particle. [latex]v(t)= \sin t - \cos t, s(0) = 0[/latex].

Solution

[latex]s(t) = 1 - \cos t - \sin t[/latex]

28.  [latex]f(x)=2x+6 \cos x,F(\pi )={\pi }^{2}+2[/latex]

Graph the following functions by hand. Make sure to label the inflection points, critical numbers, zeros, and asymptotes.

29.  [latex]y=\frac{1}{x{(x+1)}^{2}}[/latex]

Solution

This graph has vertical asymptotes at x = 0 and x = -1. The first part of the function occurs in the third quadrant with a horizontal asymptote at y = 0. The function decreases quickly from near (-5, 0) to near the vertical asymptote (-1, ∞). On the other side of the asymptote, the function is roughly U-shaped and pointed down in the third quadrant between x = -1 and x = 0 with maximum near (-0.4, -6). On the other side of the x = 0 asympotote, the function decreases from its vertical asymptote near (0, ∞) and to approach the horizontal asymptote y = 0.
Inflection points: none; critical numbers: [latex]x=-\frac{1}{3};[/latex] zeros: none; vertical asymptotes: [latex]x=-1,[/latex] [latex]x=0;[/latex] horizontal asymptote: [latex]y=0[/latex]

30.  [latex]y=x-\sqrt{4-{x}^{2}}[/latex]

For the following exercises, sketch the graph of [latex]f[/latex] by finding the following:

  1. Determine the domain of the function.
  2. Determine the [latex]x[/latex]– and [latex]y[/latex]-intercepts.
  3. Determine any horizontal or vertical asymptotes.
  4. Determine the intervals where [latex]f[/latex] is increasing and where [latex]f[/latex] is decreasing. Determine whether [latex]f[/latex] has any local extrema.
  5. Determine the intervals where [latex]f[/latex] is concave up and where [latex]f[/latex] is concave down.
  6. Determine all inflection points (if any).

31. [latex]f(x) = \frac{(x-2)(x+1)}{(x-1)^2}, f'(x) = \frac{5-x}{(x-1)^3}, f''(x) = \frac{2x-14}{(x-1)^4}[/latex]

Solution

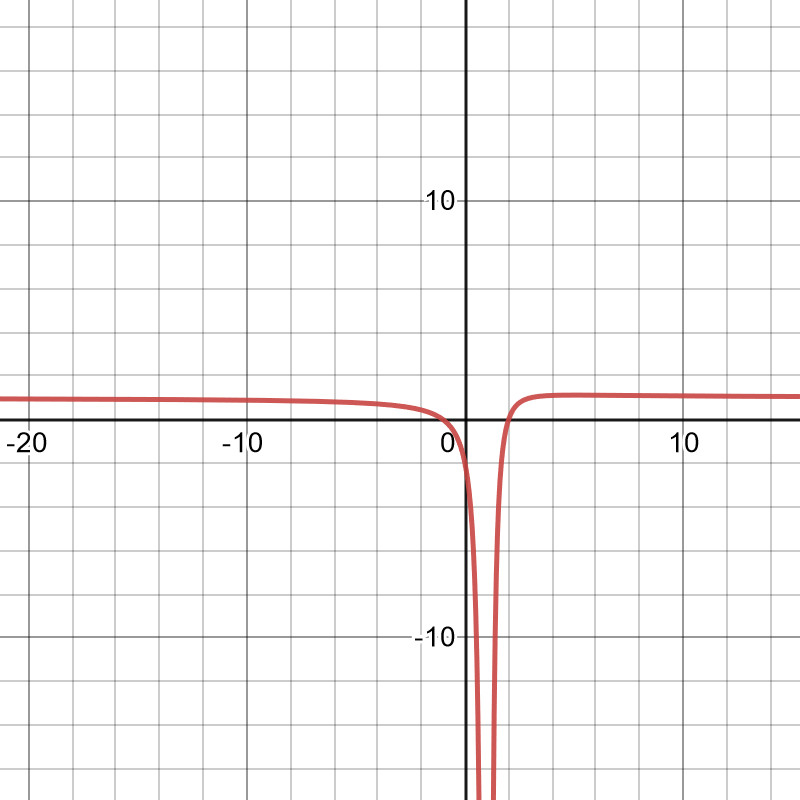
32. [latex]f(x) = \frac{4x}{(x+1)^2}, f'(x) = \frac{4(1-x)}{(x+1)^3}, f''(x) = \frac{8(x-2)}{(x+1)^4}[/latex]

33. [latex]f(x) = 5 \ln (x+6), f'(x) = \frac{5}{x+6}, f''(x) = \frac{-5}{(x+6)^2}[/latex]

Solution

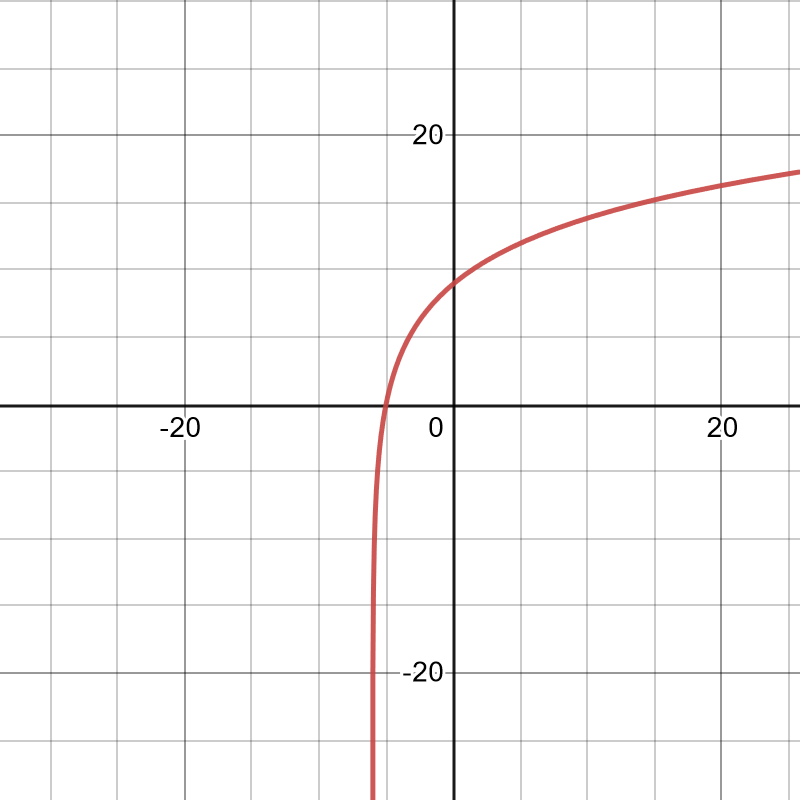
34. [latex]f(x) = \frac{9-x^2}{9+x^2}, f'(x) = \frac{-36x}{(9+x^2)^2}, f''(x) = \frac{-108(3-x^2)}{(9+x^2)^3}[/latex]

35. [latex]f(x) = \frac{2x}{e^{2x}}, f'(x) = \frac{2(1-2x)}{e^{2x}}, f''(x) = \frac{-8(1-x)}{e^{2x}}[/latex]

Solution

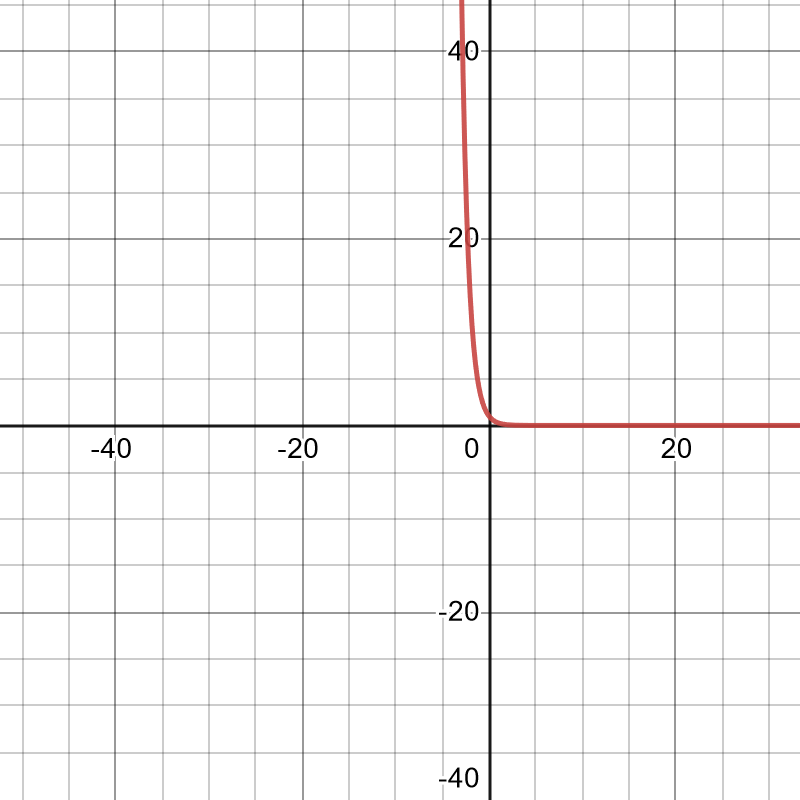
36. [latex]f(x) = 3x^2-\ln(x+7), f'(x) = 6x - \frac{1}{x+7}, f''(x) = 6 + \frac{1}{(x+7)^2}[/latex]

37. [latex]f(x) = \frac{(x+3)(x+2)}{x^2+1}, f'(x) = \frac{-5(x^2+2x-1)}{(x^2+1)^2}, f''(x) = \frac{10(x^3+3x^2-3x-1)}{(x^2+1)^3}[/latex]

Solution

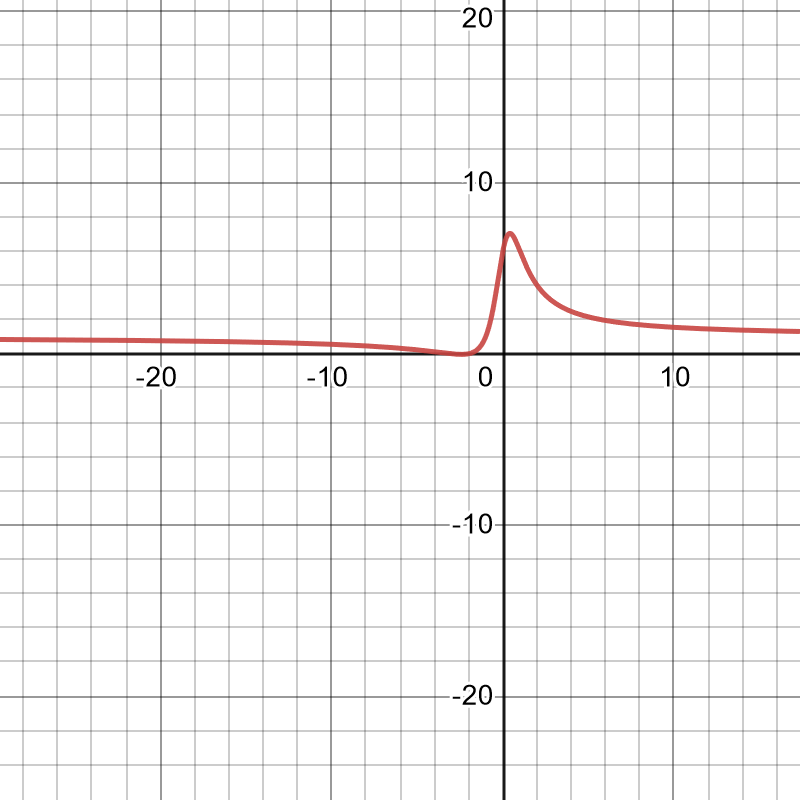
38. [latex]f(x) = \frac{x^2-9}{x^2-4}, f'(x) = \frac{10x}{(x^2-4)^2}, f''(x) = \frac{10(-3x^2-4)}{(x^2-4)^3}[/latex]

Answer the following questions.

39.  A car is being compacted into a rectangular solid. The volume is decreasing at a rate of 2 m 3 /sec. The length and width of the compactor are square, but the height is not the same length as the length and width. If the length and width walls move toward each other at a rate of 0.25 m/sec, find the rate at which the height is changing when the length and width are 2 m and the height is 1.5 m.

Solution

The height is decreasing at a rate of 0.125 m/sec

40. A rocket is launched into space; its kinetic energy is given by [latex]K(t)=(\frac{1}{2})m(t)v{(t)}^{2},[/latex] where [latex]K[/latex] is the kinetic energy in joules, [latex]m[/latex] is the mass of the rocket in kilograms, and [latex]v[/latex] is the velocity of the rocket in meters/second. Assume the velocity is increasing at a rate of 15 m/sec 2 and the mass is decreasing at a rate of 10 kg/sec because the fuel is being burned. At what rate is the rocket’s kinetic energy changing when the mass is 2000 kg and the velocity is 5000 m/sec? Give your answer in mega-Joules (MJ), which is equivalent to [latex]{10}^{6}[/latex] J.

41. Gas is escaping a spherical balloon at a rate of 4 cm[latex]^3[/latex] per minute. How fast is the surface area shrinking when then radius is 24 cm? Hint: [latex]V= \frac{4}{3} \pi r^3[/latex] and [latex]S=4 \pi r^2[/latex] .

Solution

The surface area is decreasing at a rate of [latex]\frac{1}{3} \text{cm}^2[/latex] per minute.

42. A child is flying a kite on a string. The kite is 120 ft above the ground and the wind is blowing the kite horizontally away from the child at 6 ft per second. At what rate must the child let out the string when 130 ft of string has been let out?

43. A block of ice, in the shape of a right circular cone, is melting in such a way that both its height and its radius are decreasing at the rate of 1 cm per hour. How fast is the volume decreasing when [latex]r = h = 10 \text{cm}[/latex] ?

Solution

The volume is decreasing at a rate of [latex]100 \pi \text{cm}^3[/latex] per hour.

44. A thin circular metal disk changes size (but not shape) when heated. The disk is being heated so that its radius is increasing at a rate of 0.03 mm per second. How fast is the area of the disk changing when the radius is 200 mm?

45. A person 2 m tall walks toward a lamppost on level ground at a rate of 0.5 m per second. The lamp on the post is 5 m high. How fast is the length of the person’s shadow decreasing when the person is 3 m from the post?

Solution

The length of the shadow is decreasing at a rate of [latex]\frac{1}{3}[/latex] m per sec.

46. A ladder 10 m long is leaning against a vertical wall with its other end on the ground. The top end of the ladder is sliding down the wall. When the top end of the ladder is 6 m from the ground, the ladder starts sliding down the wall at 2 m per second. How fast is the bottom of the ladder moving from the wall at this instant?

Answer the following questions.

47.  The famous Regiomontanus’ problem for angle maximization was proposed during the 15 th century. A painting hangs on a wall with the bottom of the painting a distance [latex]a[/latex] feet above eye level, and the top [latex]b[/latex] feet above eye level. What distance [latex]x[/latex] (in feet) from the wall should the viewer stand to maximize the angle subtended by the painting, [latex]\theta ?[/latex]

A point is marked eye level, and from this point a right triangle is made with adjacent side length x and opposite side length a, which is the length from the bottom of the picture to the level of the eye. A second right triangle is made from the point marked eye level, with the adjacent side being x and the other side being length b, which is the height of the picture. The angle between the two hypotenuses is marked θ.

Solution

[latex]x=\sqrt{ab}[/latex] feet

48.  An airline sells tickets from Tokyo to Detroit for [latex]$1200.[/latex] There are 500 seats available and a typical flight books 350 seats. For every [latex]$10[/latex] decrease in price, the airline observes an additional five seats sold. What should the fare be to maximize profit? How many passengers would be onboard?

49. Maximize the area of the rectangle in the first quadrant with one corner at the origin, one on the x-axis, one on the y-axis, and one on the part of the function [latex]f(x)=9-x^2[/latex] that lies in the first quadrant.

Solution

[latex]A = 6\sqrt{3}[/latex] units [latex]^2[/latex].

50. A rectangular box with square base and top is to be made to contain 1250 cm [latex]^3[/latex]. The material for the base costs 30 cents per cm [latex]^2[/latex], for the top it is 15 cents per cm [latex]^2[/latex], and for the sides it is 20 cents per cm [latex]^2[/latex]. Find the dimensions of the box that minimize the cost to construct the box.

51. Find the points on the parabola [latex]y+x^2 = 6[/latex] closest to the point [latex](0,3).[/latex]

Solution

[latex](\pm \frac{\sqrt{10}}{2}, \frac{7}{2})[/latex]

52. You have 1500 cm [latex]^2[/latex] of cardboard to make a box with a square base and an open top. Find the largest possible volume of the box.

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Calculus Volume 1 Copyright © 2016 by OSCRiceUniversity is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book