Learning Objectives

  • Calculate the derivative of an inverse function.
  • Recognize the derivatives of the standard inverse trigonometric functions.

In this section we explore the relationship between the derivative of a function and the derivative of its inverse. For functions whose derivatives we already know, we can use this relationship to find derivatives of inverses without having to use the limit definition of the derivative. In particular, we will apply the formula for derivatives of inverse functions to trigonometric functions. This formula may also be used to extend the power rule to rational exponents.

The Derivative of an Inverse Function

We begin by considering a function and its inverse. If [latex]f(x)[/latex] is both invertible and differentiable, it seems reasonable that the inverse of [latex]f(x)[/latex] is also differentiable. (Figure) shows the relationship between a function [latex]f(x)[/latex] and its inverse [latex]f^{-1}(x)[/latex]. Look at the point [latex](a,f^{-1}(a))[/latex] on the graph of [latex]f^{-1}(x)[/latex] having a tangent line with a slope of [latex](f^{-1})^{\prime}(a)=\frac{p}{q}[/latex]. This point corresponds to a point [latex](f^{-1}(a),a)[/latex] on the graph of [latex]f(x)[/latex] having a tangent line with a slope of [latex]f^{\prime}(f^{-1}(a))=\frac{q}{p}[/latex]. Thus, if [latex]f^{-1}(x)[/latex] is differentiable at [latex]a[/latex], then it must be the case that

[latex](f^{-1})^{\prime}(a)=\frac{1}{f^{\prime}(f^{-1}(a))}[/latex].
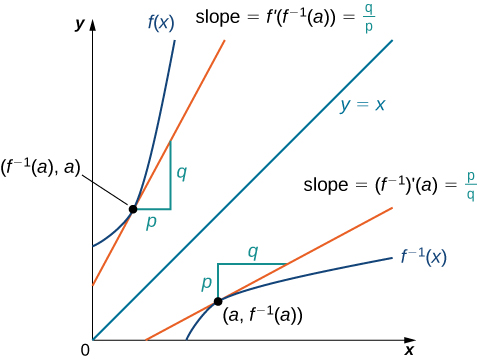
This graph shows a function f(x) and its inverse f-1(x). These functions are symmetric about the line y = x. The tangent line of the function f(x) at the point (f-1(a), a) and the tangent line of the function f-1(x) at (a, f-1(a)) are also symmetric about the line y = x. Specifically, if the slope of one were p/q, then the slope of the other would be q/p. Lastly, their derivatives are also symmetric about the line y = x.
Figure 1. The tangent lines of a function and its inverse are related; so, too, are the derivatives of these functions.

We may also derive the formula for the derivative of the inverse by first recalling that [latex]x=f(f^{-1}(x))[/latex]. Then by differentiating both sides of this equation (using the chain rule on the right), we obtain

[latex]1=f^{\prime}(f^{-1}(x))(f^{-1})^{\prime}(x))[/latex].

Solving for [latex](f^{-1})^{\prime}(x)[/latex], we obtain

[latex](f^{-1})^{\prime}(x)=\frac{1}{f^{\prime}(f^{-1}(x))}[/latex].

We summarize this result in the following theorem.

Inverse Function Theorem

Let [latex]f(x)[/latex] be a function that is both invertible and differentiable. Let [latex]y=f^{-1}(x)[/latex] be the inverse of [latex]f(x)[/latex]. For all [latex]x[/latex] satisfying [latex]f^{\prime}(f^{-1}(x))\ne 0[/latex],

[latex]\frac{dy}{dx}=\frac{d}{dx}(f^{-1}(x))=(f^{-1})^{\prime}(x)=\frac{1}{f^{\prime}(f^{-1}(x))}[/latex].

Alternatively, if [latex]y=g(x)[/latex] is the inverse of [latex]f(x)[/latex], then

[latex]g(x)=\frac{1}{f^{\prime}(g(x))}[/latex].

Applying the Inverse Function Theorem

Use the Inverse Function Theorem to find the derivative of [latex]g(x)=\frac{x+2}{x}[/latex]. Compare the resulting derivative to that obtained by differentiating the function directly.

Solution

The inverse of [latex]g(x)=\frac{x+2}{x}[/latex] is [latex]f(x)=\frac{2}{x-1}[/latex]. Since [latex]g^{\prime}(x)=\frac{1}{f^{\prime}(g(x))}[/latex], begin by finding [latex]f^{\prime}(x)[/latex]. Thus,

[latex]f^{\prime}(x)=\frac{-2}{(x-1)^2}[/latex] and [latex]f^{\prime}(g(x))=\frac{-2}{(g(x)-1)^2}=\frac{-2}{(\frac{x+2}{x}-1)^2}=-\frac{x^2}{2}[/latex].

Finally,

[latex]g^{\prime}(x)=\frac{1}{f^{\prime}(g(x))}=-\frac{2}{x^2}[/latex].

We can verify that this is the correct derivative by applying the quotient rule to [latex]g(x)[/latex] to obtain

[latex]g^{\prime}(x)=-\frac{2}{x^2}[/latex].

Use the inverse function theorem to find the derivative of [latex]g(x)=\frac{1}{x+2}.[/latex] Compare the result obtained by differentiating [latex]g(x)[/latex] directly.

Hint

Use the preceding example as a guide.

[latex]g^{\prime}(x)=-\frac{1}{(x+2)^2}[/latex]

 

Applying the Inverse Function Theorem

Use the inverse function theorem to find the derivative of [latex]g(x)=\sqrt[3]{x}[/latex].

Solution

The function [latex]g(x)=\sqrt[3]{x}[/latex] is the inverse of the function [latex]f(x)=x^3[/latex]. Since [latex]g^{\prime}(x)=\frac{1}{f^{\prime}(g(x))}[/latex], begin by finding [latex]f^{\prime}(x)[/latex]. Thus,

[latex]f^{\prime}(x)=3x^2[/latex] and [latex]f^{\prime}(g(x))=3(\sqrt[3]{x})^2=3x^{2/3}[/latex].

Finally,

[latex]g^{\prime}(x)=\frac{1}{3x^{2/3}}=\frac{1}{3}x^{-2/3}[/latex].

Find the derivative of [latex]g(x)=\sqrt[5]{x}[/latex] by applying the inverse function theorem.

Hint

Use the fact that [latex]g(x)[/latex] is the inverse of [latex]f(x)=x^5[/latex].

Solution

[latex]g(x)=\frac{1}{5}x^{-4/5}[/latex]

From the previous example, we see that we can use the inverse function theorem to extend the power rule to exponents of the form [latex]\frac{1}{n}[/latex], where [latex]n[/latex] is a positive integer. This extension will ultimately allow us to differentiate [latex]x^q[/latex], where [latex]q[/latex] is any rational number.

Extending the Power Rule to Rational Exponents

The power rule may be extended to rational exponents. That is, if [latex]n[/latex] is a positive integer, then

[latex]\frac{d}{dx}(x^{1/n})=\frac{1}{n}x^{(1/n)-1}[/latex].

Also, if [latex]n[/latex] is a positive integer and [latex]m[/latex] is an arbitrary integer, then

[latex]\frac{d}{dx}(x^{m/n})=\frac{m}{n}x^{(m/n)-1}[/latex].

Proof

The function [latex]g(x)=x^{1/n}[/latex] is the inverse of the function [latex]f(x)=x^n[/latex]. Since [latex]g^{\prime}(x)=\frac{1}{f^{\prime}(g(x))}[/latex], begin by finding [latex]f^{\prime}(x)[/latex]. Thus,

[latex]f^{\prime}(x)=nx^{n-1}[/latex] and [latex]f^{\prime}(g(x))=n(x^{1/n})^{n-1}=nx^{(n-1)/n}[/latex].

Finally,

[latex]g^{\prime}(x)=\frac{1}{nx^{(n-1)/n}}=\frac{1}{n}x^{(1-n)/n}=\frac{1}{n}x^{(1/n)-1}[/latex].

To differentiate [latex]x^{m/n}[/latex] we must rewrite it as [latex](x^{1/n})^m[/latex] and apply the chain rule. Thus,

[latex]\frac{d}{dx}(x^{m/n})=\frac{d}{dx}((x^{1/n})^m)=m(x^{1/n})^{m-1} \cdot \frac{1}{n}x^{(1/n)-1}=\frac{m}{n}x^{(m/n)-1}[/latex]. [latex]_\blacksquare[/latex]

Applying the Power Rule to a Rational Power

Find the equation of the line tangent to the graph of [latex]y=x^{2/3}[/latex] at [latex]x=8[/latex].

Solution

First find [latex]\frac{dy}{dx}[/latex] and evaluate it at [latex]x=8[/latex]. Since

[latex]\frac{dy}{dx}=\frac{2}{3}x^{-1/3}[/latex] and [latex]\frac{dy}{dx}|_{x=8}=\frac{1}{3}[/latex]

the slope of the tangent line to the graph at [latex]x=8[/latex] is [latex]\frac{1}{3}[/latex].

Substituting [latex]x=8[/latex] into the original function, we obtain [latex]y=4[/latex]. Thus, the tangent line passes through the point [latex](8,4)[/latex]. Substituting into the point-slope formula for a line and solving for [latex]y[/latex], we obtain the tangent line

[latex]y=\frac{1}{3}x+\frac{4}{3}[/latex].

Find the derivative of [latex]s(t)=\sqrt{2t+1}[/latex].

Hint

Rewrite as [latex]s(t)=(2t+1)^{1/2}[/latex] and use the chain rule.

Solution

[latex]s^{\prime}(t)=(2t+1)^{-1/2}[/latex]

Derivatives of Inverse Trigonometric Functions

We now turn our attention to finding derivatives of inverse trigonometric functions. These derivatives will prove invaluable in the study of integration later in this text. The derivatives of inverse trigonometric functions are quite surprising in that their derivatives are actually algebraic functions. Previously, derivatives of algebraic functions have proven to be algebraic functions and derivatives of trigonometric functions have been shown to be trigonometric functions. Here, for the first time, we see that the derivative of a function need not be of the same type as the original function.

Derivative of the Inverse Sine Function

Use the inverse function theorem to find the derivative of [latex]g(x)=\sin^{-1} x[/latex].

Solution

Since for [latex]x[/latex] in the interval [latex][-\frac{\pi}{2},\frac{\pi}{2}], \, f(x)= \sin x[/latex] is the inverse of [latex]g(x)= \sin^{-1} x[/latex], begin by finding [latex]f^{\prime}(x)[/latex]. Since

[latex]f^{\prime}(x)= \cos x[/latex] and [latex]f^{\prime}(g(x))= \cos (\sin^{-1} x)=\sqrt{1-x^2}[/latex],

we see that

[latex]g^{\prime}(x)=\frac{d}{dx}(\sin^{-1} x)=\frac{1}{f^{\prime}(g(x))}=\frac{1}{\sqrt{1-x^2}}[/latex].

Analysis

To see that [latex]\cos (\sin^{-1} x)=\sqrt{1-x^2}[/latex], consider the following argument. Set [latex]\sin^{-1} x=\theta[/latex]. In this case, [latex]\sin \theta =x[/latex] where [latex]-\frac{\pi}{2}\le \theta \le \frac{\pi}{2}[/latex]. We begin by considering the case where [latex]0 < \theta < \frac{\pi}{2}[/latex]. Since [latex]\theta[/latex] is an acute angle, we may construct a right triangle having acute angle [latex]\theta[/latex], a hypotenuse of length 1, and the side opposite angle [latex]\theta[/latex] having length [latex]x[/latex]. From the Pythagorean theorem, the side adjacent to angle [latex]\theta[/latex] has length [latex]\sqrt{1-x^2}[/latex]. This triangle is shown in (Figure) . Using the triangle, we see that [latex]\cos (\sin^{-1} x)= \cos \theta =\sqrt{1-x^2}[/latex].

A right triangle with angle θ, opposite side x, hypotenuse 1, and adjacent side equal to the square root of the quantity (1 – x2).
Figure 2 . Using a right triangle having acute angle [latex]\theta[/latex], a hypotenuse of length 1, and the side opposite angle [latex]\theta[/latex] having length [latex]x[/latex], we can see that [latex]\cos (\sin^{-1} x)= \cos \theta =\sqrt{1-x^2}[/latex].

In the case where [latex]-\frac{\pi}{2} < \theta < 0[/latex], we make the observation that [latex]0 < -\theta < \frac{\pi}{2}[/latex] and hence [latex]\cos (\sin^{-1} x)= \cos \theta = \cos (-\theta )=\sqrt{1-x^2}[/latex].

Now if [latex]\theta =\frac{\pi}{2}[/latex] or [latex]\theta =-\frac{\pi}{2}, \, x=1[/latex] or [latex]x=-1[/latex], and since in either case [latex]\cos \theta =0[/latex] and [latex]\sqrt{1-x^2}=0[/latex], we have

[latex]\cos (\sin^{-1} x)= \cos \theta =\sqrt{1-x^2}[/latex].

Consequently, in all cases, [latex]\cos (\sin^{-1} x)=\sqrt{1-x^2}[/latex].

Applying the Chain Rule to the Inverse Sine Function

Apply the chain rule to the formula derived in (Figure) to find the derivative of [latex]h(x)=\sin^{-1} (g(x))[/latex] and use this result to find the derivative of [latex]h(x)=\sin^{-1}(2x^3)[/latex].

Solution

Applying the chain rule to [latex]h(x)=\sin^{-1} (g(x))[/latex], we have

[latex]h^{\prime}(x)=\frac{1}{\sqrt{1-(g(x))^2}}g^{\prime}(x)[/latex].

Now let [latex]g(x)=2x^3[/latex], so [latex]g^{\prime}(x)=6x[/latex]. Substituting into the previous result, we obtain

[latex]\begin{array}{ll} h^{\prime}(x) & =\frac{1}{\sqrt{1-4x^6}} \cdot 6x \\ & =\frac{6x}{\sqrt{1-4x^6}}. \end{array}[/latex]

Use the inverse function theorem to find the derivative of [latex]g(x)=\tan^{-1} x[/latex].

Hint

The inverse of [latex]g(x)[/latex] is [latex]f(x)= \tan x[/latex]. Use (Figure) as a guide.

Solution

[latex]g^{\prime}(x)=\frac{1}{1+x^2}[/latex]

The derivatives of the remaining inverse trigonometric functions may also be found by using the inverse function theorem. These formulas are provided in the following theorem.

Derivatives of Inverse Trigonometric Functions

[latex]\begin{array}{lllll}\frac{d}{dx}(\sin^{-1} x)=\large \frac{1}{\sqrt{1-x^2}} & & & & \frac{d}{dx}(\cos^{-1} x)=\large \frac{-1}{\sqrt{1-x^2}} \\ \frac{d}{dx}(\tan^{-1} x)=\large \frac{1}{1+x^2} & & & & \frac{d}{dx}(\cot^{-1} x)=\large \frac{-1}{1+x^2} \\ \frac{d}{dx}(\sec^{-1} x)=\large \frac{1}{|x|\sqrt{x^2-1}} & & & & \frac{d}{dx}(\csc^{-1} x)=\large \frac{-1}{|x|\sqrt{x^2-1}} \end{array}[/latex]

Applying Differentiation Formulas to an Inverse Tangent Function

Find the derivative of [latex]f(x)=\tan^{-1} (x^2)[/latex].

Solution

Let [latex]g(x)=x^2[/latex], so [latex]g^{\prime}(x)=2x[/latex]. Substituting into (Figure) , we obtain

[latex]f^{\prime}(x)=\frac{1}{1+(x^2)^2} \cdot (2x)[/latex].

Simplifying, we have

[latex]f^{\prime}(x)=\frac{2x}{1+x^4}[/latex].

Applying Differentiation Formulas to an Inverse Sine Function

Find the derivative of [latex]h(x)=x^2 \sin^{-1} x[/latex].

Solution

By applying the product rule, we have

[latex]h^{\prime}(x)=2x \sin^{-1} x+\frac{1}{\sqrt{1-x^2}} \cdot x^2[/latex].

Find the derivative of [latex]h(x)= \cos^{-1} (3x-1)[/latex].

Hint

Use (Figure) . with [latex]g(x)=3x-1[/latex]

Solution

[latex]h^{\prime}(x)=\frac{-3}{\sqrt{6x-9x^2}}[/latex]

Applying the Inverse Tangent Function

The position of a particle at time [latex]t[/latex] is given by [latex]s(t)= \tan^{-1}(\frac{1}{t})[/latex] for [latex]t\ge \frac{1}{2}[/latex]. Find the velocity of the particle at time [latex]t=1[/latex].

Solution

Begin by differentiating [latex]s(t)[/latex] in order to find [latex]v(t)[/latex]. Thus,

[latex]v(t)=s^{\prime}(t)=\frac{1}{1+(\frac{1}{t})^2} \cdot \frac{-1}{t^2}[/latex].

Simplifying, we have

[latex]v(t)=-\frac{1}{t^2+1}[/latex].

Thus, [latex]v(1)=-\frac{1}{2}[/latex].

Find the equation of the line tangent to the graph of [latex]f(x)= \sin^{-1} x[/latex] at [latex]x=0[/latex].

Hint

[latex]f^{\prime}(0)[/latex] gives the slope of the tangent line.

Solution

[latex]y=x[/latex]

Key Concepts

  • The inverse function theorem allows us to compute derivatives of inverse functions without using the limit definition of the derivative.
  • We can use the inverse function theorem to develop differentiation formulas for the inverse trigonometric functions.

Key Equations

  • Inverse function theorem
    [latex](f^{-1})^{\prime}(x)=\frac{1}{f^{\prime}(f^{-1}(x))}[/latex] whenever [latex]f^{\prime}(f^{-1}(x))\ne 0[/latex] and [latex]f(x)[/latex] is differentiable.
  • Power rule with rational exponents
    [latex]\frac{d}{dx}(x^{m/n})=\frac{m}{n}x^{(m/n)-1}[/latex].
  • Derivative of inverse sine function
    [latex]\frac{d}{dx}(\sin^{-1} x)=\frac{1}{\sqrt{1-x^2}}[/latex]
  • Derivative of inverse cosine function
    [latex]\frac{d}{dx}(\cos^{-1} x)=\frac{-1}{\sqrt{1-x^2}}[/latex]
  • Derivative of inverse tangent function
    [latex]\frac{d}{dx}(\tan^{-1} x)=\frac{1}{1+x^2}[/latex]
  • Derivative of inverse cotangent function
    [latex]\frac{d}{dx}(\cot^{-1} x)=\frac{-1}{1+x^2}[/latex]
  • Derivative of inverse secant function
    [latex]\frac{d}{dx}(\sec^{-1} x)=\frac{1}{|x|\sqrt{x^2-1}}[/latex]
  • Derivative of inverse cosecant function
    [latex]\frac{d}{dx}(\csc^{-1} x)=\frac{-1}{|x|\sqrt{x^2-1}}[/latex]

For the following exercises, use the graph of [latex]y=f(x)[/latex] to

  1. sketch the graph of [latex]y=f^{-1}(x)[/latex], and
  2. use part a. to estimate [latex](f^{-1})^{\prime}(1)[/latex].
1.
 A straight line passing through (0, -3) and (3, 3).

2.
 A curved line starting at (-2, 0) and passing through (-1, 1) and (2, 2).

Solution

a.

A curved line starting at (-3, 0) and passing through (-2, 1) and (1, 2). There is another curved line that is symmetric with this about the line x = y. That is, it starts at (0, -3) and passes through (1, -2) and (2, 1).
b. [latex](f^{-1})^{\prime}(1) \approx 2[/latex]

3.
 A curved line starting at (4, 0) and passing through (0, 1) and (-1, 4).

4.
 A quarter circle starting at (0, 4) and ending at (4, 0).

Solution

a.

A quarter circle starting at (0, 4) and ending at (4, 0).
b. [latex](f^{-1})^{\prime}(1) \approx -1/\sqrt{3}[/latex]

For the following exercises, use the functions [latex]y=f(x)[/latex] to find

  1. [latex]\frac{df}{dx}[/latex] at [latex]x=a[/latex] and
  2. [latex]x=f^{-1}(y)[/latex].
  3. Then use part b. to find [latex]\frac{df^{-1}}{dy}[/latex] at [latex]y=f(a)[/latex].

5.  [latex]f(x)=6x-1, \, x=-2[/latex]

6.  [latex]f(x)=2x^3-3, \, x=1[/latex]

Solution

a. 6
b. [latex]x=f^{-1}(y)=(\frac{y+3}{2})^{1/3}[/latex]
c. [latex]\frac{1}{6}[/latex]

7.  [latex]f(x)=9-x^2, \, 0\le x\le 3, \, x=2[/latex]

8.  [latex]f(x)= \sin x, \, x=0[/latex]

Solution

a. 1
b. [latex]x=f^{-1}(y)= \sin^{-1} y[/latex]
c. 1

For each of the following functions, find [latex](f^{-1})^{\prime}(a)[/latex].

9.  [latex]f(x)=x^2+3x+2, \, x\ge -1, \, a=2[/latex]

10.  [latex]f(x)=x^3+2x+3, \, a=0[/latex]

Solution

[latex]\frac{1}{5}[/latex]

11.  [latex]f(x)=x+\sqrt{x}, \, a=2[/latex]

12.  [latex]f(x)=x-\frac{2}{x}, \, x < 0, \, a=1[/latex]

Solution

[latex]\frac{1}{3}[/latex]

13.  [latex]f(x)=x + \sin x, \, a=0[/latex]

14.  [latex]f(x)= \tan x+3x^2, \, a=0[/latex]

Solution

1

For each of the given functions [latex]y=f(x)[/latex],

  1. find the slope of the tangent line to its inverse function [latex]f^{-1}[/latex] at the indicated point [latex]P[/latex], and
  2. find the equation of the tangent line to the graph of [latex]f^{-1}[/latex] at the indicated point.

15.  [latex]f(x)=\frac{4}{1+x^2}, \, P(2,1)[/latex]

16.  [latex]f(x)=\sqrt{x-4}, \, P(2,8)[/latex]

Solution

a. 4
b. [latex]y=4x[/latex]

17.  [latex]f(x)=(x^3+1)^4, \, P(16,1)[/latex]

18.  [latex]f(x)=-x^3-x+2, \, P(-8,2)[/latex]

Solution

a. [latex]-\frac{1}{13}[/latex]
b. [latex]y=-\frac{1}{13}x+\frac{18}{13}[/latex]

19.  [latex]f(x)=x^5+3x^3-4x-8, \, P(-8,1)[/latex]

For the following exercises, find [latex]\frac{dy}{dx}[/latex] for the given function.

20.  [latex]y= \sin^{-1}(x^2)[/latex]

Solution

[latex]\large \frac{2x}{\sqrt{1-x^4}}[/latex]

21.  [latex]y= \cos^{-1}(\sqrt{x})[/latex]

22.  [latex]y= \sec^{-1}(\frac{1}{x})[/latex]

Solution

[latex]\large \frac{-1}{\sqrt{1-x^2}}[/latex]

23.  [latex]y=\sqrt{\csc^{-1} x}[/latex]

24.  [latex]y=(1 + \tan^{-1} x)^3[/latex]

Solution

[latex]\large \frac{3(1 + \tan^{-1} x)^2}{1+x^2}[/latex]

25.  [latex]y= \cos^{-1}(2x) \cdot \sin^{-1}(2x)[/latex]

26.  [latex]y=\frac{1}{\tan^{-1}(x)}[/latex]

Solution

[latex]\large \frac{-1}{(1+x^2)(\tan^{-1} x)^2}[/latex]

27.  [latex]y= \sec^{-1}(-x)[/latex]

28.  [latex]y= \cot^{-1} \sqrt{4-x^2}[/latex]

Solution

[latex]\large \frac{x}{(5-x^2)\sqrt{4-x^2}}[/latex]

29.  [latex]y=x \cdot \csc^{-1} x[/latex]

For the following exercises, use the given values to find [latex](f^{-1})^{\prime}(a)[/latex].

30.  [latex]f(\pi)=0, \, f^{\prime}(\pi)=-1, \, a=0[/latex]

Solution

-1

31.  [latex]f(6)=2, \, f^{\prime}(6)=\frac{1}{3}, \, a=2[/latex]

32.  [latex]f(\frac{1}{3})=-8, \, f^{\prime}(\frac{1}{3})=2, \, a=-8[/latex]

Solution

[latex]\frac{1}{2}[/latex]

33.  [latex]f(\sqrt{3})=\frac{1}{2}, \, f^{\prime}(\sqrt{3})=\frac{2}{3}, \, a=\frac{1}{2}[/latex]

34.  [latex]f(1)=-3, \, f^{\prime}(1)=10, \, a=-3[/latex]

Solution

[latex]\frac{1}{10}[/latex]

35.  [latex]f(1)=0, \, f^{\prime}(1)=-2, \, a=0[/latex]

36. [T] The position of a moving hockey puck after [latex]t[/latex] seconds is [latex]s(t)= \tan^{-1} t[/latex] where [latex]s[/latex] is in meters.

  1. Find the velocity of the hockey puck at any time [latex]t[/latex].
  2. Find the acceleration of the puck at any time [latex]t[/latex].
  3. Evaluate a. and b. for [latex]t=2,4[/latex], and 6 seconds.
  4. What conclusion can be drawn from the results in c.?

Solution

a. [latex]v(t)=\frac{1}{1+t^2}[/latex]
b. [latex]a(t)=\frac{-2t}{(1+t^2)^2}[/latex]
c. [latex]v(2)=0.2, \, v(4)=0.06, \, v(6)=0.03; \, a(2)=-0.16, \, a(4)=-0.028, \, a(6)=-0.0088[/latex]
d. The hockey puck is decelerating/slowing down at 2, 4, and 6 seconds.

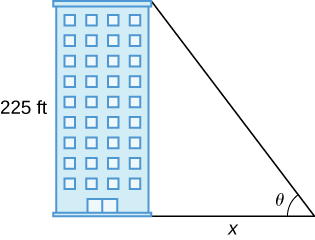
37. [T] A building that is 225 feet tall casts a shadow of various lengths [latex]x[/latex] as the day goes by. An angle of elevation [latex]\theta[/latex] is formed by lines from the top and bottom of the building to the tip of the shadow, as seen in the following figure. Find the rate of change of the angle of elevation [latex]\frac{d\theta}{dx}[/latex] when [latex]x=272[/latex] feet.

A building is shown with height 225 ft. A triangle is made with the building height as the opposite side from the angle θ. The adjacent side has length x.

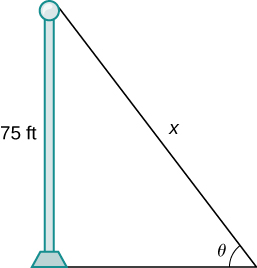
38. [T] A pole stands 75 feet tall. An angle [latex]\theta[/latex] is formed when wires of various lengths of [latex]x[/latex] feet are attached from the ground to the top of the pole, as shown in the following figure. Find the rate of change of the angle [latex]\frac{d\theta}{dx}[/latex] when a wire of length 90 feet is attached.

A flagpole is shown with height 75 ft. A triangle is made with the flagpole height as the opposite side from the angle θ. The hypotenuse has length x.

-0.0168 radians per foot

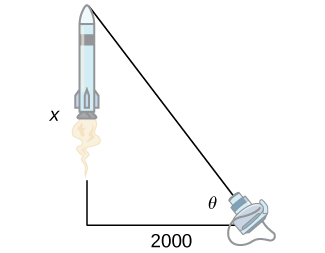
39. [T] A television camera at ground level is 2000 feet away from the launching pad of a space rocket that is set to take off vertically, as seen in the following figure. The angle of elevation of the camera can be found by [latex]\theta = \tan^{-1}(\frac{x}{2000})[/latex], where [latex]x[/latex] is the height of the rocket. Find the rate of change of the angle of elevation after launch when the camera and the rocket are 5000 feet apart.

A rocket is shown with in the air with the distance from its nose to the ground being x. A triangle is made with the rocket height as the opposite side from the angle θ. The adjacent side has length 2000.

40. [T] A local movie theater with a 30-foot-high screen that is 10 feet above a person’s eye level when seated has a viewing angle [latex]\theta[/latex] (in radians) given by [latex]\theta = \cot^{-1}(\frac{x}{40})- \cot^{-1}(\frac{x}{10})[/latex],

where [latex]x[/latex] is the distance in feet away from the movie screen that the person is sitting, as shown in the following figure.

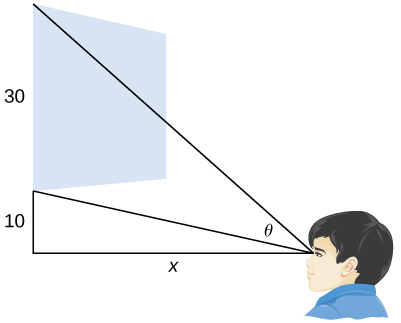
A person is shown with a right triangle coming from their eye (the right angle being on the opposite side from the eye), with height 10 and base x. There is a line drawn from the eye to the top of the screen, which makes an angle θ with the triangle’s hypotenuse. The screen has a height of 30.

  1. Find [latex]\frac{d\theta}{dx}[/latex].
  2. Evaluate [latex]\frac{d\theta}{dx}[/latex] for [latex]x=5,10,15[/latex], and 20.
  3. Interpret the results in b.
  4. Evaluate [latex]\frac{d\theta}{dx}[/latex] for [latex]x=25,30,35[/latex], and 40
  5. Interpret the results in d. At what distance [latex]x[/latex] should the person sit to maximize his or her viewing angle?
a. [latex]\frac{d\theta}{dx}=\frac{10}{100+x^2}-\frac{40}{1600+x^2}[/latex]
b. [latex]\frac{18}{325}, \, \frac{9}{340}, \, \frac{42}{4745}, \, 0[/latex]
c. As a person moves farther away from the screen, the viewing angle is increasing, which implies that as he or she moves farther away, his or her screen vision is widening.
d. [latex]-\frac{54}{12905}, \, -\frac{3}{500}, \, -\frac{198}{29945}, \, -\frac{9}{1360}[/latex]
e. As the person moves beyond 20 feet from the screen, the viewing angle is decreasing. The optimal distance the person should sit for maximizing the viewing angle is 20 feet.

 

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Calculus Volume 1 Copyright © 2016 by OSCRiceUniversity is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book