Chapter 7: Angular Kinematics

Problems & Exercises

7.1 Rotation Angle and Angular Velocity

  1. Semi-trailer trucks have an odometer on one hub of a trailer wheel. The hub is weighted so that it does not rotate, but it contains gears to count the number of wheel revolutions—it then calculates the distance traveled. If the wheel has a 1.15 m diameter and goes through 200,000 rotations, how many kilometers should the odometer read?
    Solution: 723 km
  2. Microwave ovens rotate at a rate of about 6 rev/min. What is this in revolutions per second? What is the angular velocity in radians per second?
  3. An automobile with 0.260 m radius tires travels 80,000 km before wearing them out. How many revolutions do the tires make, neglecting any backing up and any change in radius due to wear?
    Solution: [latex]5×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{rotations}[/latex]
  4. (a) What is the period of rotation of Earth in seconds?
    (b) What is the angular velocity of Earth?
    (c) Given that Earth has a radius of [latex]6\text{.}4×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] at its equator, what is the linear velocity at Earth’s surface?
  5. A baseball pitcher brings his arm forward during a pitch, rotating the forearm about the elbow. If the velocity of the ball in the pitcher’s hand is 35.0 m/s and the ball is 0.300 m from the elbow joint, what is the angular velocity of the forearm?
    Solution: 117 rad/s
  6. In lacrosse, a ball is thrown from a net on the end of a stick by rotating the stick and forearm about the elbow. If the angular velocity of the ball about the elbow joint is 30.0 rad/s and the ball is 1.30 m from the elbow joint, what is the velocity of the ball?
  7. A truck with 0.420-m-radius tires travels at 32.0 m/s. What is the angular velocity of the rotating tires in radians per second? What is this in rev/min?
    Solution: 76.2 rad/s; 728 rpm
  8. Integrated Concepts When kicking a football, the kicker rotates his leg about the hip joint.
    (a) If the velocity of the tip of the kicker’s shoe is 35.0 m/s and the hip joint is 1.05 m from the tip of the shoe, what is the shoe tip’s angular velocity?
    (b) The shoe is in contact with the initially stationary 0.500 kg football for 20.0 ms. What average force is exerted on the football to give it a velocity of 20.0 m/s?
    (c) Find the maximum range of the football, neglecting air resistance.
    Solution: (a) 33.3 rad/s; (b) 500 N; (c) 40.8 m
  9. Construct Your Own Problem: Consider an amusement park ride in which participants are rotated about a vertical axis in a cylinder with vertical walls. Once the angular velocity reaches its full value, the floor drops away and friction between the walls and the riders prevents them from sliding down. Construct a problem in which you calculate the necessary angular velocity that assures the riders will not slide down the wall. Include a free body diagram of a single rider. Among the variables to consider are the radius of the cylinder and the coefficients of friction between the riders’ clothing and the wall.
  10. *A track star runs a 400-m race on a 400-m circular track in 45 s. What is his angular velocity assuming a constant speed?
    Solution:[latex]\omega =\frac{2πrad}{45.0s}=0.14rad/s[/latex]

7.2 Angular Acceleration

  1. At its peak, a tornado is 60.0 m in diameter and carries 500 km/h winds. What is its angular velocity in revolutions per second?
    Solution: [latex]\omega =0\text{.}\text{737 rev/s}[/latex]
  2. Integrated Concepts: An ultracentrifuge accelerates from rest to 100,000 rpm in 2.00 min.
    (a) What is its angular acceleration in [latex]{\text{rad/s}}^{2}[/latex]?
    (b) What is the tangential acceleration of a point 9.50 cm from the axis of rotation?
    (c) What is the radial acceleration in [latex]{\text{m/s}}^{2}[/latex] and multiples of [latex]g[/latex] of this point at full rpm?
  3. Integrated Concepts: You have a grindstone (a disk) that is 90.0 kg, has a 0.340-m radius, and is turning at 90.0 rpm, and you press a steel axe against it with a radial force of 20.0 N.
    (a) Assuming the kinetic coefficient of friction between steel and stone is 0.20, calculate the angular acceleration of the grindstone.
    (b) How many turns will the stone make before coming to rest?
    Solution: (a) [latex]-0\text{.}{\text{26 rad/s}}^{2}[/latex]; (b) [latex]\text{27}\phantom{\rule{0.25em}{0ex}}\text{rev}[/latex]
  4. Unreasonable Results: You are told that a basketball player spins the ball with an angular acceleration of [latex]\text{100}{\text{ rad/s}}^{2}[/latex].
    (a) What is the ball’s final angular velocity if the ball starts from rest and the acceleration lasts 2.00 s?
    (b) What is unreasonable about the result?
    (c) Which premises are unreasonable or inconsistent?

7.3 Centripetal Acceleration

  1. A fairground ride spins its occupants inside a flying saucer-shaped container. If the horizontal circular path the riders follow has an 8.00 m radius, at how many revolutions per minute will the riders be subjected to a centripetal acceleration whose magnitude is 1.50 times that due to gravity?
    Solution: 12.9 rev/min
  2. A runner taking part in the 200 m dash must run around the end of a track that has a circular arc with a radius of curvature of 30 m. If he completes the 200 m dash in 23.2 s and runs at constant speed throughout the race, what is the magnitude of his centripetal acceleration as he runs the curved portion of the track?
  3. Taking the age of Earth to be about [latex]4×{\text{10}}^{9}[/latex] years and assuming its orbital radius of [latex]1.5 ×{\text{10}}^{11}[/latex] m has not changed and is circular, calculate the approximate total distance Earth has traveled since its birth (in a frame of reference stationary with respect to the Sun).
    Solution: [latex]4×{\text{10}}^{\text{21}}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex]
  4. The propeller of a World War II fighter plane is 2.30 m in diameter.
    (a) What is its angular velocity in radians per second if it spins at 1200 rev/min?
    (b) What is the linear speed of its tip at this angular velocity if the plane is stationary on the tarmac?
    (c) What is the centripetal acceleration of the propeller tip under these conditions? Calculate it in meters per second squared and convert to multiples of [latex]g[/latex].
  5. An ordinary workshop grindstone has a radius of 7.50 cm and rotates at 6500 rev/min.
    (a) Calculate the magnitude of the centripetal acceleration at its edge in meters per second squared and convert it to multiples of [latex]g[/latex].
    (b) What is the linear speed of a point on its edge?
    Solution: (a) [latex]3.\text{47}×{\text{10}}^{\text{4}}\phantom{\rule{0.25em}{0ex}}\text{m}/{\text{s}}^{2}[/latex], [latex]3.\text{55}×{\text{10}}^{\text{3}}\phantom{\rule{0.25em}{0ex}}g[/latex]; (b) [latex]51.\text{1}\phantom{\rule{0.25em}{0ex}}\text{m}/{\text{s}}^{}[/latex]
  6. Helicopter blades withstand tremendous stresses. In addition to supporting the weight of a helicopter, they are spun at rapid rates and experience large centripetal accelerations, especially at the tip.
    (a) Calculate the magnitude of the centripetal acceleration at the tip of a 4.00 m long helicopter blade that rotates at 300 rev/min.
    (b) Compare the linear speed of the tip with the speed of sound (taken to be 340 m/s).
  7. Olympic ice skaters are able to spin at about 5 rev/s.
    (a) What is their angular velocity in radians per second?
    (b) What is the centripetal acceleration of the skater’s nose if it is 0.120 m from the axis of rotation?
    (c) An exceptional skater named Dick Button was able to spin much faster in the 1950s than anyone since—at about 9 rev/s. What was the centripetal acceleration of the tip of his nose, assuming it is at 0.120 m radius?
    (d) Comment on the magnitudes of the accelerations found. It is reputed that Button ruptured small blood vessels during his spins.
    Solution: (a) [latex]\text{31.4 rad/s}[/latex]; (b) [latex]\text{118 m/s}[/latex]; (c) [latex]\text{384 m/s}[/latex]; (d)The centripetal acceleration felt by Olympic skaters is 12 times larger than the acceleration due to gravity. That’s quite a lot of acceleration in itself. The centripetal acceleration felt by Button’s nose was 39.2 times larger than the acceleration due to gravity. It is no wonder that he ruptured small blood vessels in his spins.
  8. What percentage of the acceleration at Earth’s surface is the acceleration due to gravity at the position of a satellite located 300 km above Earth?
  9. Verify that the linear speed of an ultracentrifuge is about 0.50 km/s, and Earth in its orbit is about 30 km/s by calculating:
    (a) The linear speed of a point on an ultracentrifuge 0.100 m from its center, rotating at 50,000 rev/min.
    (b) The linear speed of Earth in its orbit about the Sun (use data from the text on the radius of Earth’s orbit and approximate it as being circular).
    Solution: (a) 0.524 km/s; (b) 29.7 km/s
  10. At takeoff, a commercial jet has a 60.0 m/s speed. Its tires have a diameter of 0.850 m.
    (a) At how many rev/min are the tires rotating?
    (b) What is the centripetal acceleration at the edge of the tire?
    (c) With what force must a determined [latex]1\text{.}\text{00}×{\text{10}}^{-\text{15}}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex] bacterium cling to the rim?
    (d) Take the ratio of this force to the bacterium’s weight.
    Solution: (a) [latex]\text{1.35}×{\text{10}}^{\text{3}}\phantom{\rule{0.25em}{0ex}}\text{rpm}[/latex]; (b) [latex]\text{8.47}×{\text{10}}^{\text{3}}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{\text{2}}[/latex]; (c) [latex]\text{8.47}×{\text{10}}^{\text{–12}}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex]; (d) [latex]\text{865}[/latex]
  11. Integrated Concepts: Riders in an amusement park ride shaped like a Viking ship hung from a large pivot are rotated back and forth like a rigid pendulum. Sometime near the middle of the ride, the ship is momentarily motionless at the top of its circular arc. The ship then swings down under the influence of gravity.
    (a) Assuming negligible friction, find the speed of the riders at the bottom of its arc, given the system’s center of mass travels in an arc having a radius of 14.0 m and the riders are near the center of mass.
    (b) What is the centripetal acceleration at the bottom of the arc?
    (c) Draw a free body diagram of the forces acting on a rider at the bottom of the arc.
    (d) Find the force exerted by the ride on a 60.0 kg rider and compare it to her weight.
    (e) Discuss whether the answer seems reasonable.
    Solution: (a) [latex]\text{16.6}\phantom{\rule{0.25em}{0ex}}\text{m/s}[/latex]; (b) [latex]\text{19.6}\phantom{\rule{0.25em}{0ex}}\text{m}/{\text{s}}^{2}[/latex]; (c)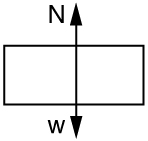A rectangle with a base longer than the height. A vertical line with arrowheads on both ends passes through the rectangle, bisecting the horizontal sides. The top of the arrow is labeled N, and the bottom is labeled w.; (d) [latex]\text{1}.\text{76}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{N or 3}.\text{00}\phantom{\rule{0.25em}{0ex}}w[/latex] , that is, the normal force (upward) is three times her weight.; (e) This answer seems reasonable, since she feels like she’s being forced into the chair MUCH stronger than just by gravity.
  12. Unreasonable Results: A mother pushes her child on a swing so that his speed is 9.00 m/s at the lowest point of his path. The swing is suspended 2.00 m above the child’s center of mass.
    (a) What is the magnitude of the centripetal acceleration of the child at the low point?
    (b) What is the magnitude of the force the child exerts on the seat if his mass is 18.0 kg?
    (c) What is unreasonable about these results?
    (d) Which premises are unreasonable or inconsistent?
    Solution: (a) [latex]\text{40}.5\phantom{\rule{0.25em}{0ex}}\text{m}/{\text{s}}^{2}[/latex]; (b) 905 N; (c) The force in part (b) is very large. The acceleration in part (a) is too much, about 4 g; (d) The speed of the swing is too large. At the given velocity at the bottom of the swing, there is enough kinetic energy to send the child all the way over the top, ignoring friction.
  13. *A fairground ride spins its occupants inside a flying saucer-shaped container. If the horizontal circular path the riders follow has an 8.00-m radius, at how many revolutions per minute are the riders subjected to a centripetal acceleration equal to that of gravity?
    Solution: aC=78.4, v=8.85m/s, T=5.68s , 

     which is 0.176 rev/s=10.6 rev/min

  14. *A runner taking part in the 200-m dash must run around the end of a track that has a circular arc with a radius of curvature of 30.0 m. The runner starts the race at a constant speed. If she completes the 200-m dash in 23.2 s and runs at constant speed throughout the race, what is her centripetal acceleration as she runs the curved portion of the track?

7.4 Centripetal Force

  1. (a) A 22.0 kg child is riding a playground merry-go-round that is rotating at 40.0 rev/min. What centripetal force must she exert to stay on if she is 1.25 m from its center?
    (b) What centripetal force does she need to stay on an amusement park merry-go-round that rotates at 3.00 rev/min if she is 8.00 m from its center?
    (c) Compare each force with her weight.
    Solution: (a) 483 N; (b) 17.4 N; (c) 2.24 times her weight, 0.0807 times her weight
  2. Calculate the centripetal force on the end of a 100 m (radius) wind turbine blade that is rotating at 0.5 rev/s. Assume the mass is 4 kg.
  3. What is the ideal banking angle for a gentle turn of 1.20 km radius on a highway with a 105 km/h speed limit (about 65 mi/h), assuming everyone travels at the limit?
    Solution: [latex]4\text{.}\text{14º}[/latex]
  4. What is the ideal speed to take a 100 m radius curve banked at a 20.0° angle?
  5. (a) What is the radius of a bobsled turn banked at 75.0° and taken at 30.0 m/s, assuming it is ideally banked?
    (b) Calculate the centripetal acceleration.
    (c) Does this acceleration seem large to you?
    Solution: (a) 24.6 m; (b) [latex]36.6 m/{\text{s}}^{2}[/latex]; (c) [latex]{a}_{\text{c}}=3.73\phantom{\rule{0.25em}{0ex}}\mathrm{g.}[/latex] This does not seem too large, but it is clear that bobsledders feel a lot of force on them going through sharply banked turns.
  6. Part of riding a bicycle involves leaning at the correct angle when making a turn, as seen in the figure. To be stable, the force exerted by the ground must be on a line going through the center of gravity. The force on the bicycle wheel can be resolved into two perpendicular components—friction parallel to the road (this must supply the centripetal force), and the vertical normal force (which must equal the system’s weight).
    (a) Show that [latex]\theta[/latex] (as defined in the figure) is related to the speed [latex]v[/latex] and radius of curvature [latex]r[/latex] of the turn in the same way as for an ideally banked roadway—that is, [latex]\theta ={\text{tan}}^{\text{–1}}{v}^{2}/\mathrm{rg}[/latex]
    (b) Calculate [latex]\theta[/latex] for a 12.0 m/s turn of radius 30.0 m (as in a race).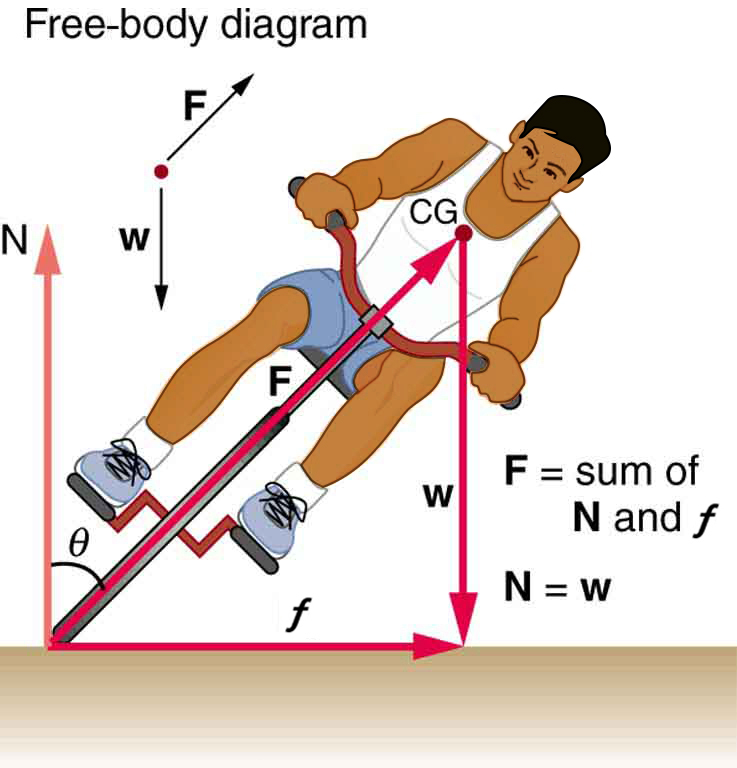

    The given figure shows a boy riding a bicycle, from the front. The boy is sliding leftward to his left. Three vectors are shown. One is from the bottom the front cycle wheel to the right depicting centripetal force, another one is from the same point drawn vertically upward showing the force N, making an angle theta with the slope of the front cycle wheel. The third vector is drawn from the chest of the boy to vertically downward to the bottom showing his weight, w. An arrow from the bottom of the wheel to the chest point of the boy is also shown depicting the slope of the bicycle with force F exerting on it. A free-body diagram is also given alongside the figure showing the direction of weight and force vectors. And the values of net F equals to sum of N and centripetal force, and N equals to weight W also given alongside on the right.
    A bicyclist negotiating a turn on level ground must lean at the correct angle—the ability to do this becomes instinctive. The force of the ground on the wheel needs to be on a line through the center of gravity. The net external force on the system is the centripetal force. The vertical component of the force on the wheel cancels the weight of the system while its horizontal component must supply the centripetal force. This process produces a relationship among the angle θ, the speed v, and the radius of curvature r of the turn similar to that for the ideal banking of roadways
  7. A large centrifuge, like the one shown in the figure (a), is used to expose aspiring astronauts to accelerations similar to those experienced in rocket launches and atmospheric reentries.
    (a) At what angular velocity is the centripetal acceleration [latex]\mathrm{10}\phantom{\rule{0.25em}{0ex}}g[/latex] if the rider is 15.0 m from the center of rotation?
    (b) The rider’s cage hangs on a pivot at the end of the arm, allowing it to swing outward during rotation as shown in figure(b). At what angle [latex]\theta[/latex] below the horizontal will the cage hang when the centripetal acceleration is [latex]\mathrm{10}\phantom{\rule{0.25em}{0ex}}g[/latex]? (Hint: The arm supplies centripetal force and supports the weight of the cage. Draw a free body diagram of the forces to see what the angle [latex]\theta[/latex] should be.)

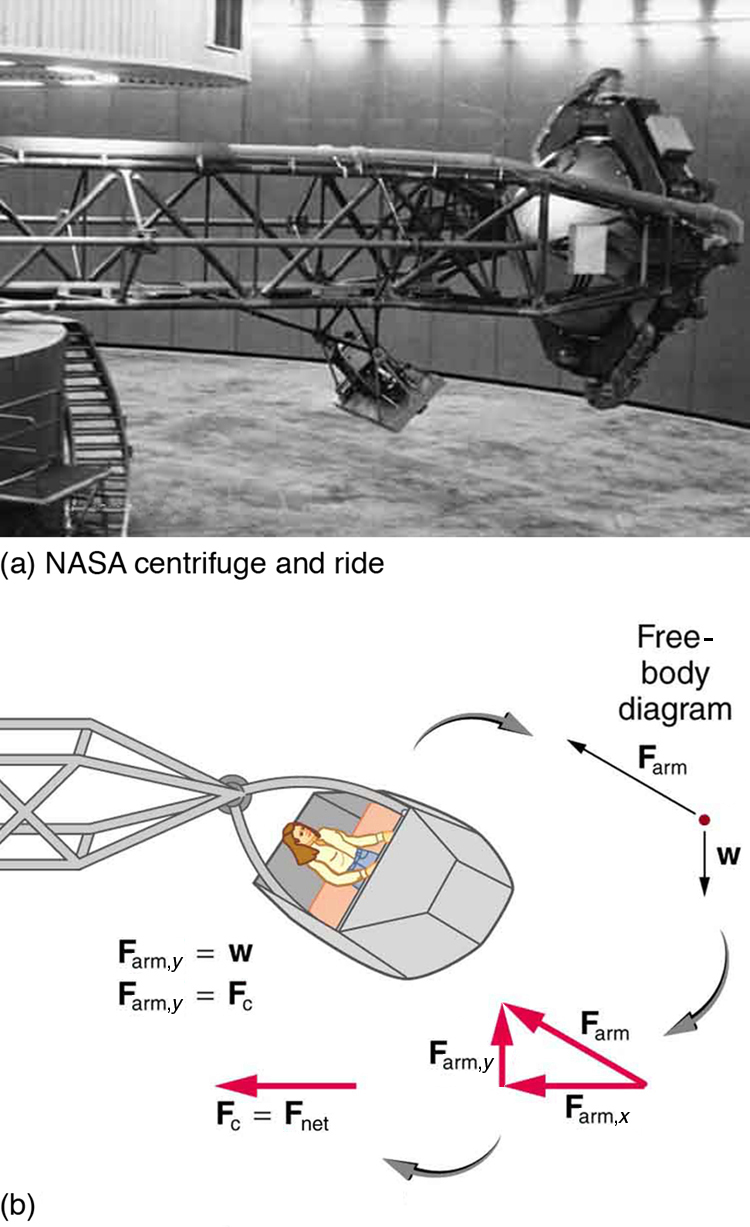
    Figure a shows a NASA centrifuge n a big hall. In figure b, there is a girl sitting in the cage of the centrifuge. The centripetal force on the cage is directed toward left. The direction of the weight of the cage is downward and the force on the arm is directed in north-west direction.
    (a) NASA centrifuge used to subject trainees to accelerations similar to those experienced in rocket launches and reentries. (credit: NASA) (b) Rider in cage showing how the cage pivots outward during rotation. This allows the total force exerted on the rider by the cage to be along its axis at all times. 

    Solution: (a) 2.56 rad/s; (b) [latex]5.71º[/latex] 

  8. Modern roller coasters have vertical loops like the one shown in the figure. The radius of curvature is smaller at the top than on the sides so that the downward centripetal acceleration at the top will be greater than the acceleration due to gravity, keeping the passengers pressed firmly into their seats. What is the speed of the roller coaster at the top of the loop if the radius of curvature there is 15.0 m and the downward acceleration of the car is 1.50 g?
    A teardrop shaped loop of a roller coaster is shown. The car of the roller coaster starts from the point A near the right of the base and covers the teardrop portion of the roller coaster and move to a point D at the left of base. Near the top of tear drop portion an upward arrow is shown labeled as r-minimum. Also at a point near the base toward A there is a label called r-maximum. The wire frame of the base is also shown.
    Teardrop-shaped loops are used in the latest roller coasters so that the radius of curvature gradually decreases to a minimum at the top. This means that the centripetal acceleration builds from zero to a maximum at the top and gradually decreases again. A circular loop would cause a jolting change in acceleration at entry, a disadvantage discovered long ago in railroad curve design. With a small radius of curvature at the top, the centripetal acceleration can more easily be kept greater than g so that the passengers do not lose contact with their seats nor do they need seat belts to keep them in place.
  9. Unreasonable Results: (a) Calculate the minimum coefficient of friction needed for a car to negotiate an unbanked 50.0 m radius curve at 30.0 m/s.
    (b) What is unreasonable about the result?
    (c) Which premises are unreasonable or inconsistent?
    Solution: (a) 1.84; (b) A coefficient of friction this much greater than 1 is unreasonable; (c) The assumed speed is too great for the tight curve.
  10. Integrated Concepts: If a car takes a banked curve at less than the ideal speed, friction is needed to keep it from sliding toward the inside of the curve (a real problem on icy mountain roads). (a) Calculate the ideal speed to take a 100 m radius curve banked at 15.0º. (b) What is the minimum coefficient of friction needed for a frightened driver to take the same curve at 20.0 km/h?
    Solution: (a) 16.2 m/s; (b) 0.234

7.5 Relating Angular and Translational Quantities

  1. A man stands on a merry-go-round that is rotating at 2.5 rad/s. If the coefficient of static friction between the man’s shoes and the merry-go-round is [latex]{\mu }_{\text{S}}=0.5[/latex], how far from the axis of rotation can he stand without sliding?
    Solution: [latex]r=0.78\,\text{m}[/latex]
  2. An ultracentrifuge accelerates from rest to 100,000 rpm in 2.00 min.
    (a) What is the average angular acceleration in [latex]{\text{rad/s}}^{2}[/latex]?
    (b) What is the tangential acceleration of a point 9.50 cm from the axis of rotation?
    (c) What is the centripetal acceleration in [latex]{\text{m/s}}^{2}[/latex] and multiples of g of this point at full rpm?
    (d) What is the total distance travelled by a point 9.5 cm from the axis of rotation of the ultracentrifuge?
  3. A wind turbine is rotating counterclockwise at 0.5 rev/s and slows to a stop in 10 s. Its blades are 20 m in length.
    (a) What is the angular acceleration of the turbine?
    (b) What is the centripetal acceleration of the tip of the blades at [latex]t=0\,\text{s?}[/latex]
    (c) What is the magnitude and direction of the total linear acceleration of the tip of the blades at [latex]t=0\,\text{s?}[/latex]
    Solution: (a) [latex]\alpha =-0.314\,\text{rad}\text{/}{\text{s}}^{2}[/latex]; (b) [latex]{a}_{\text{c}}=197.4\,\text{m}\text{/}{\text{s}}^{2}[/latex]; (c) [latex]a=\sqrt{{a}_{\text{c}}^{2}+{a}_{\text{t}}^{2}}=\sqrt{{197.4}^{2}+{(-6.28)}^{2}}=197.5\,\text{m}\text{/}{\text{s}}^{2}[/latex], [latex]\theta ={\text{tan}}^{-1}\frac{-6.28}{197.4}=-1.8\text{°}[/latex] in the clockwise direction from the centripetal acceleration vector
  4. What is
    (a) the angular speed and
    (b) the linear speed of a point on Earth’s surface at latitude [latex]30\text{°}[/latex] N. Take the radius of the Earth to be 6309 km.
    (c) At what latitude would your linear speed be 10 m/s?
  5. A child with mass 30 kg sits on the edge of a merry-go-round at a distance of 3.0 m from its axis of rotation. The merry-go-round accelerates from rest up to 0.4 rev/s in 10 s. If the coefficient of static friction between the child and the surface of the merry-go-round is 0.6, does the child fall off before 5 s?
    Solution: [latex]ma=40.0\,\text{kg}(5.1\,\text{m}\text{/}{\text{s}}^{2})=204.0\,\text{N}[/latex]. The maximum friction force is [latex]{\mu }_{\text{S}}N=0.6(40.0\,\text{kg})(9.8\,\text{m}\text{/}{\text{s}}^{2})=235.2\,\text{N}[/latex] so the child does not fall off yet.
  6. A bicycle wheel with radius 0.3m rotates from rest to 3 rev/s in 5 s. What is the magnitude and direction of the total acceleration vector at the edge of the wheel at 1.0 s?
  7. The angular velocity of a flywheel with radius 1.0 m varies according to [latex]\omega (t)=2.0t[/latex]. Plot [latex]{a}_{\text{c}}(t)\,\text{and}\,{a}_{\text{t}}(t)[/latex] from [latex]t=\text{0 to 3.0 s}[/latex] for [latex]r=1.0\,\text{m}[/latex]. Analyze these results to explain when [latex]{a}_{\text{c}}\gg {a}_{\text{t}}[/latex] and when [latex]{a}_{\text{c}}\ll {a}_{\text{t}}[/latex] for a point on the flywheel at a radius of 1.0 m.
    Solution: [latex]\begin{array}{ccc}\hfill {v}_{\text{t}}& =\hfill & r\omega =1.0(2.0t)\,\text{m/s}\hfill \\ \hfill {a}_{\text{c}}& =\hfill & \frac{{v}_{t}^{2}}{r}=\frac{{(2.0t)}^{2}}{1.0\,\text{m}}=4.0{t}^{2}\text{m}\text{/}{\text{s}}^{2}\hfill \\ \hfill {a}_{\text{t}}(t)& =\hfill & r\alpha (t)=r\frac{d\omega }{dt}=1.0\,\text{m}(2.0)=2.0\,\text{m}\text{/}{\text{s}}^{2}.\hfill \end{array}[/latex]
    Plotting both accelerations gives
    Figure shows a linear acceleration in meters per second squared plotted as a function of time in seconds. Centripetal starts at the origin of the coordinate system and grows exponentially with time. Tangential is positive and remains constant with time
    The tangential acceleration is constant, while the centripetal acceleration is time dependent, and increases with time to values much greater than the tangential acceleration after t = 1s. For times less than 0.7 s and approaching zero the centripetal acceleration is much less than the tangential acceleration.

7.7 Kinematics of Rotational Motion

  1. With the aid of a string, a gyroscope is accelerated from rest to 32 rad/s in 0.40 s.
    (a) What is its angular acceleration in rad/s2?
    (b) How many revolutions does it go through in the process?
    Solution: (a) [latex]80\phantom{\rule{0.25em}{0ex}}{\text{rad/s}}^{2}[/latex]; (b) 1.0 rev
  2. Suppose a piece of dust finds itself on a CD. If the spin rate of the CD is 500 rpm, and the piece of dust is 4.3 cm from the center, what is the total distance traveled by the dust in 3 minutes? (Ignore accelerations due to getting the CD rotating.)
  3. A gyroscope slows from an initial rate of 32.0 rad/s at a rate of [latex]0\text{.}\text{700}{\text{ rad/s}}^{2}[/latex].
    (a) How long does it take to come to rest?
    (b) How many revolutions does it make before stopping?
    Solution: (a) 45.7 s; (b) 116 rev
  4. During a very quick stop, a car decelerates at [latex]7\text{.}\text{00}{\text{ m/s}}^{2}[/latex].
    (a) What is the angular acceleration of its 0.280-m-radius tires, assuming they do not slip on the pavement?
    (b) How many revolutions do the tires make before coming to rest, given their initial angular velocity is [latex]\text{95}\text{.}0\text{ rad/s}[/latex]?
    (c) How long does the car take to stop completely?
    (d) What distance does the car travel in this time?
    (e) What was the car’s initial velocity?
    (f) Do the values obtained seem reasonable, considering that this stop happens very quickly?
  5. Everyday application: Suppose a yo-yo has a center shaft that has a 0.250 cm radius and that its string is being pulled.
    (a) If the string is stationary and the yo-yo accelerates away from it at a rate of [latex]1\text{.}\text{50}{\text{ m/s}}^{2}[/latex], what is the angular acceleration of the yo-yo?
    (b) What is the angular velocity after 0.750 s if it starts from rest?
    (c) The outside radius of the yo-yo is 3.50 cm. What is the tangential acceleration of a point on its edge?

    The figure shows the left arm of a man with tattoo imprints and wearing a glove. He is circulating a yo-yo toy, which is in mid air and connected by the string to his hand. Some people are standing in the background watching the yo-yo trick.
    Yo-yos are amusing toys that display significant physics and are engineered to enhance performance based on physical laws. (credit: Beyond Neon, Flickr)

    Solution: (a) [latex]6{\text{00 rad/s}}^{2}[/latex]; (b) 450 rad/s; (c) 21.0 m/s

Additional Problems

    1. A 30.0-g ball at the end of a string is swung in a vertical circle with a radius of 25.0 cm. The tangential velocity is 200.0 cm/s. Find the tension in the string:
      (a) at the top of the circle,
      (b) at the bottom of the circle, and
      (c) at a distance of 12.5 cm from the center of the circle (r=12.5cm).
      Solution: (a) 0.186 N; (b) 0.774 N; (c) 0.48 N
    2. A stunt cyclist rides on the interior of a cylinder 12 m in radius. The coefficient of static friction between the tires and the wall is 0.68. Find the value of the minimum speed for the cyclist to perform the stunt.
      Solution: 13 m/s
    3. A piece of bacon starts to slide down the pan when one side of a pan is raised up 5.0 cm. If the length of the pan from pivot to the raising point is 23.5 cm, what is the coefficient of static friction between the pan and the bacon?
      Solution: 0.21
    4. *A cyclist is riding such that the wheels of the bicycle have a rotation rate of 3.0 rev/s. If the cyclist brakes such that the rotation rate of the wheels decrease at a rate of 0.3rev/s2, how long does it take for the cyclist to come to a complete stop?
      Solution: [latex]\text{Δ}t = 10.0 s[/latex]
    5. *The angular acceleration of a rotating rigid body is given by [latex]\alpha = (2.0 - 3.0t)rad/{\text{s}}^{2}[/latex] If the body starts rotating from rest at t=0,
      (a) what is the angular velocity?
      (b) Angular position?
      (c) What angle does it rotate through in 10 s?
      (d) Where does the vector perpendicular to the axis of rotation indicating 0° at t=0 lie at t=10 s
      Solution: (a) [latex]\omega=2.0t−1.5t^2[/latex]; (b) [latex]\theta={\text{t}}^{2}−{\text{0.5}}^{3}[/latex]; (c) [latex]\theta=−400.0rad[/latex]; (d) the vector is at [latex]−0.66(360°)=−237.6°[/latex]

License

Icon for the Creative Commons Attribution 4.0 International License

Introduction to Biomechanics Copyright © 2022 by Rob Pryce is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book