Chapter 6: Linear Momentum and Collisions

6.5 Inelastic Collisions in One Dimension

Authors: Paul Peter Urone, Roger Hinrichs
Adapted by: Rob Pryce, Alix Blacklin

Learning Objectives

By the end of this section, you will be able to:

  • Define and inelastic collisions.
  • Define and explain coefficient of restitution.
  • Use coefficient of restitution to solve collision problems
  • Apply an understanding of collisions to sports.
  • Determine recoil velocity and loss in kinetic energy given mass and initial velocity.

We have seen that in an elastic collision, internal kinetic energy is conserved. An inelastic collision is one in which the internal kinetic energy changes (it is not conserved). This lack of conservation means that the forces between colliding objects may remove or add internal kinetic energy. Work done by internal forces may change the forms of energy within a system. For inelastic collisions, such as when colliding objects stick together, this internal work may transform some internal kinetic energy into heat transfer. Or it may convert stored energy into internal kinetic energy, such as when exploding bolts separate a satellite from its launch vehicle.

Inelastic Collision

An inelastic collision is one in which the internal kinetic energy changes (it is not conserved).

 

The figure below shows an example of an inelastic collision. Two objects that have equal masses head toward one another at equal speeds and then stick together. Their total internal kinetic energy is initially [latex]\frac{1}{2}{\text{mv}}^{2}+\frac{1}{2}{\text{mv}}^{2}={\text{mv}}^{2}[/latex]. The two objects come to rest after sticking together, conserving momentum. But the internal kinetic energy is zero after the collision. A collision in which the objects stick together is sometimes called a perfectly inelastic collision because it reduces internal kinetic energy more than does any other type of inelastic collision. In fact, such a collision reduces internal kinetic energy to the minimum it can have while still conserving momentum.

Perfectly Inelastic Collision

A collision in which the objects stick together is sometimes called “perfectly inelastic.” This results in the maximal loss of internal kinetic energy, which is converted to other forms of energy (e.g., heat, sound).

 

 

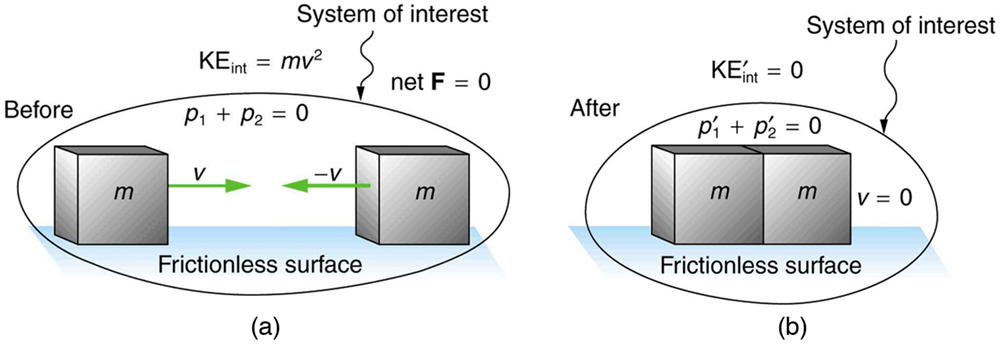
The system of interest contains two equal masses with mass m. One moves to the right and the other moves to the left with the same magnitude of velocity represented by V. Due to this their total momentum and net force remains zero. The internal kinetic energy is mv power 2. After collision the system of interest has no net velocity, no total momentum and no internal kinetic energy. This is true for all inelastic collisions.
Figure 6.8 An inelastic one-dimensional two-object collision. Momentum is conserved, but internal kinetic energy is not conserved. (a) Two objects of equal mass initially head directly toward one another at the same speed. (b) The objects stick together (a perfectly inelastic collision), and so their final velocity is zero. The internal kinetic energy of the system changes in any inelastic collision and is reduced to zero in this example.

In perfectly inelastic collisions both objects will have the same post-collision velocity ([latex]v\prime_1 = v\prime_2[/latex]). Therefore, the equation for conservation of momentum, [latex]{m}_{1}{v}_{1}+{m}_{2}{v}_{2}={m}_{1}{v\prime }_{1}+{m}_{2}{v\prime }_{2}\phantom{\rule{0.25em}{0ex}}\phantom{\rule{0.25em}{0ex}}\phantom{\rule{0.25em}{0ex}}[/latex], which normally has two unknowns ([latex]v\prime_1[/latex] and [latex]v\prime_2[/latex]) has only one unknown (the post-collision velocity of both objects and be written:

[latex]{m}_{1}{v}_{1}+{m}_{2}{v}_{2}=\left(m_1+ m_2\right)v\prime[/latex]

Example: Calculating Velocity and Change in Kinetic Energy: Inelastic Collision of a Puck and a Goalie

(a) Find the recoil velocity of a 70.0-kg ice hockey goalie, originally at rest, who catches a 0.150-kg hockey puck slapped at him at a velocity of 35.0 m/s.
(b) How much kinetic energy is lost during the collision? Assume friction between the ice and the puck-goalie system is negligible. (See the figure below)

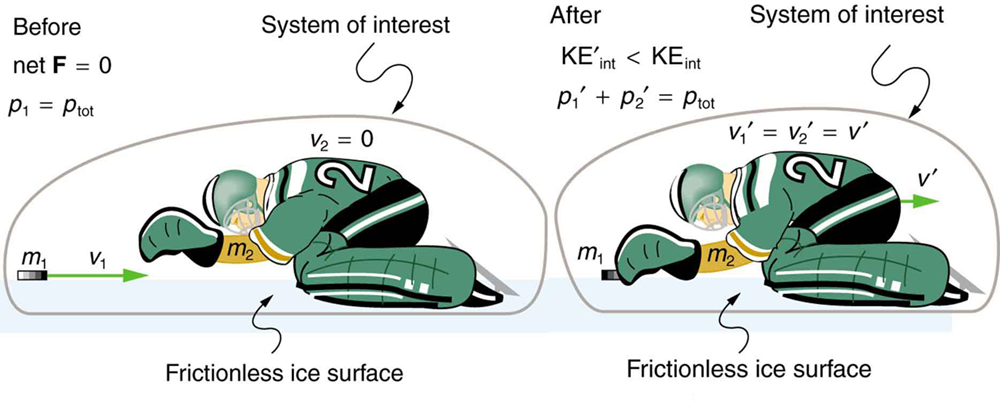
The first picture shows an ice hockey goal keeper of mass m 2 bent on his knees, turning to the left on a frictionless ice surface with zero velocity and a hockey puck of mass m 1 and velocity V 1 moving toward the right. The total momentum of the system is p 1 which is the momentum of the puck and the net force is zero. The second picture shows the goalie to catch the puck. The puck moves with velocity V 1prime and the goalie with velocity V 2 prime and their magnitudes are equal. The momentum of the puck is p 1 prime and the goalie is p 2 prime. The total momentum remains same as before collision. But the kinetic energy after collision is lesser than the kinetic energy before collision. This is true for inelastic collisions.
Figure 6.9 An ice hockey goalie catches a hockey puck and recoils backward. The initial kinetic energy of the puck is almost entirely converted to thermal energy and sound in this inelastic collision.

Strategy

Momentum is conserved because the net external force on the puck-goalie system is zero. We can thus use conservation of momentum to find the final velocity of the puck and goalie system. Note that the initial velocity of the goalie is zero and that the final velocity of the puck and goalie are the same. Once the final velocity is found, the kinetic energies can be calculated before and after the collision and compared as requested.

Solution for (a)

Momentum is conserved because the net external force on the puck-goalie system is zero.

Conservation of momentum is

[latex]{p}_{1}+{p}_{2}={p\prime }_{1}+{p\prime }_{2}[/latex]

or

[latex]{m}_{1}{v}_{1}+{m}_{2}{v}_{2}={m}_{1}{v\prime }_{1}+{m}_{2}{v\prime }_{2}.[/latex]

Because the goalie is initially at rest, we know [latex]{v}_{2}=0[/latex]. Because the goalie catches the puck, the final velocities are equal, or [latex]{v\prime }_{1}={v\prime }_{2}=v\prime[/latex]. Thus, the conservation of momentum equation simplifies to

[latex]{m}_{1}{v}_{1}=\left({m}_{1}+{m}_{2}\right)v\prime .[/latex]

Solving for [latex]v\prime[/latex] yields

[latex]v\prime =\frac{{m}_{1}}{{m}_{1}+{m}_{2}}{v}_{1}.[/latex]

Entering known values in this equation, we get

[latex]v\prime =\left(\frac{\text{0.150 kg}}{\text{0.150 kg}+\text{70.0 kg}}\right)\left(\text{35}\text{.0 m/s}\right)=7\text{.}\text{48}×{\text{10}}^{-2}\phantom{\rule{0.25em}{0ex}}\text{m/s}\text{.}[/latex]


Discussion for (a)

This recoil velocity is small and in the same direction as the puck’s original velocity, as we might expect.

Solution for (b)

Before the collision, the internal kinetic energy [latex]{\text{KE}}_{\text{int}}[/latex] of the system is that of the hockey puck, because the goalie is initially at rest. Therefore, [latex]{\text{KE}}_{\text{int}}[/latex] is initially

[latex]\begin{array}{lll}{\text{KE}}_{\text{int}}& =& \frac{1}{2}{\text{mv}}^{2}=\frac{1}{2}\left(0\text{.}\text{150 kg}\right){\left(\text{35}\text{.0 m/s}\right)}^{2}\\ \text{}& =& \text{91}\text{.}\text{9 J}\text{.}\end{array}[/latex]

After the collision, the internal kinetic energy is

[latex]\begin{array}{lll}{\text{KE}\prime }_{\text{int}}& =& \frac{1}{2}\left(m+M\right){v}^{2}=\frac{1}{2}\left(\text{70}\text{.}\text{15 kg}\right){\left(7\text{.}\text{48}×{\text{10}}^{-2}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)}^{2}\\ & =& \text{0.196 J.}\end{array}[/latex]

The change in internal kinetic energy is thus

[latex]\begin{array}{lll}{KE\prime }_{\text{int}}-{\text{KE}}_{\text{int}}& =& \text{0.196 J}-\text{91.9 J}\\ & =& -\text{91.7 J}\end{array}[/latex]

where the minus sign indicates that the energy was lost.

Discussion for (b)

Nearly all of the initial internal kinetic energy is lost in this perfectly inelastic collision. [latex]{\text{KE}}_{\text{int}}[/latex] is mostly converted to thermal energy and sound.

Collisions that are not perfectly inelastic

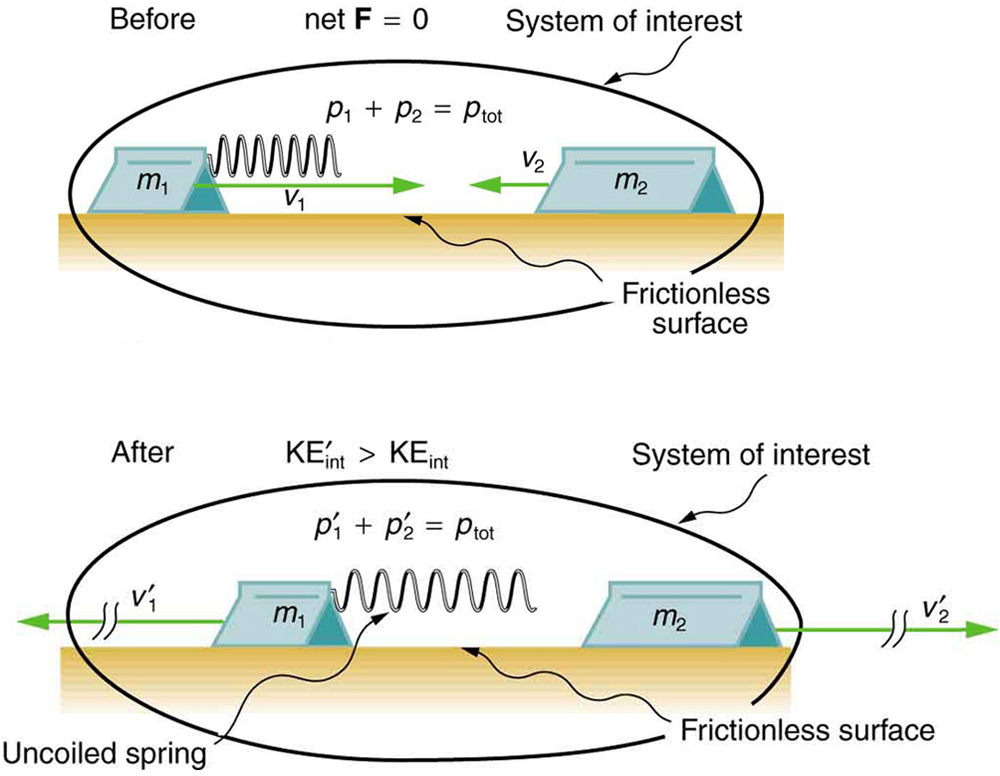
During some collisions, the objects do not stick together and less of the internal kinetic energy is removed—such as happens in most automobile accidents. Alternatively, stored energy may be converted into internal kinetic energy during a collision. The figure below shows a one-dimensional example in which two carts on an air track collide, releasing potential energy from a compressed spring. This figure deals with data from such a collision.

An uncoiled spring is connected to a glider with triangular cross sectional area of mass m 1 which moves with velocity v 1 toward the right. Another solid glider of mass m 2 and triangular cross sectional area moves toward the left with velocity V 2 on a frictionless surface. The total momentum is the sum of their individual momentum p 1 and p 2. After collision m 1 moves to the left with velocity V 1 prime and momentum p 1prime. M 2 moves to the right with velocity V 2 prime. Their individual momentum becomes p 1prime and p 2 prime but the total momentum remains the same. The internal kinetic energy after collision is greater than the kinetic energy before collision.
Figure 6.10 An air track is nearly frictionless, so that momentum is conserved. Motion is one-dimensional. In this collision, examined in the figure below, the potential energy of a compressed spring is released during the collision and is converted to internal kinetic energy.

Collisions are particularly important in sports and the sporting and leisure industry utilizes elastic and inelastic collisions. Let us look briefly at tennis. Recall that in a collision, it is momentum and not force that is important. So, a heavier tennis racquet will have the advantage over a lighter one. This conclusion also holds true for other sports—a lightweight bat (such as a softball bat) cannot hit a hardball very far.

The location of the impact of the tennis ball on the racquet is also important, as is the part of the stroke during which the impact occurs. A smooth motion results in the maximizing of the velocity of the ball after impact and reduces sports injuries such as tennis elbow. A tennis player tries to hit the ball on the “sweet spot” on the racquet, where the vibration and impact are minimized and the ball is able to be given maximal post-collision velocity. Sports science and technologies also use physics concepts such as momentum and rotational motion and vibrations.

Coefficient of Restitution

Let us look at a common everyday example to understand collisions that are not perfectly elastic or inelastic – that is, some, but not all, of the systems internal kinetic is lost (and momentum is conserved). Consider what happens when you drop a tennis ball on the ground from a given height. Does it return to the same height that you dropped it? Why not?

If the collision between the ball and the earth (the system) was perfectly elastic, we’d predict that the ball would return to the same height as it was dropped (assuming that the earth is fixed and has zero velocity or kinetic energy pre- and post-collision). And if that held, ignoring some negligible loss of velocity from drag, the ball would continue bouncing for quite a long time. However, we’ve all observed that most balls dropped quickly lose height on subsequent bounces (more than we’d predict by simply drag from the air).  How can we explain this?

We could apply what we know from projectile motion and determine that the velocity the ball bounces back from the ground (i.e. post-bounce velocity) must have been less than the velocity it hit the ground (i.e. pre-bounce velocity). Ignoring the effects of drag, the height that the tennis ball bounces would be determined by the velocity it left the ground. Therefore, some velocity (and kinetic energy) must have been lost during the collision. We also know that if we dropped different balls they would bounce to different heights – because even though they might hit the ground with the same velocity (if dropped from the same height), their post-collision velocity with the ground would be different.

We might want to express how ‘bouncy’ a ball was by constructing a ratio of the two velocities:

[latex]\text{'bounciness'} = \frac{\text{post-bounce velocity}}{\text{pre-bounce velocity}}[/latex]

Looking at the ratio we could see that balls that had the same velocity after they hit the ground would have a ‘bounciness’ = 1 and balls that didn’t bounce at all would have a ‘bounciness’ = 0. Intuitively, we’d know that most balls would have a ‘bounciness’ greater than 0 but less than 1 (since most bounce somewhat).

This ratio is also called the ‘coefficient of restitution’ and is often written as:

[latex]\lvert v_2-v_1 \rvert = e \lvert v\prime_2 - v\prime_1 \rvert[/latex],

where e = coefficient of restitution, and [latex]\lvert v_2-v_1 \rvert[/latex] and [latex]\lvert v\prime_2 - v\prime_1 \rvert[/latex] are the velocities of approach and velocities of separation, respectively. In this case, the coefficient of restitution reflects the reduction in post-collision velocities, due to a reduction in internal kinetic energy.

Coefficients of restitution are a common part of many sports. For instance, the coefficient of restitution of most striking implements such as golf clubs and baseball bats are regulated by their respective sport organizations to ensure fairness in sport (or to protect other athletes on the field of play). Similarly, coefficients of restitution are regulated in court-ball games such as basketball to ensure the interactions between the ball and court (e.g., dribbling) are similar across locations.

Finally, we can use the coefficient of restitution in two convenient ways:

1. We can express it as a function of bounce height (by using the equation: [latex]v_f^2 = v_i^2 + 2gy[/latex]), which simplifies to:

[latex]e = \sqrt{\frac{bounce height}{drop height}}[/latex]

2. We can incorporate it into equations for post-collision velocities

[latex]v\prime_1 = \frac{m_1v\prime_1 + m_2v\prime_2 + e*m_2\left(v_2 - v_1\right)}{m_1 + m_2}[/latex], and

[latex]v\prime_2 = \frac{m_1v\prime_1 + m_2v\prime_2 + e*m_2\left(v_1 - v_2\right)}{m_1 + m_2}[/latex]

 

Example: Calculating coefficient of restitution

What is the coefficient of restitution of a basketball that bounces off the court to a height of 1.31m when dropped from 1.83m?

Strategy

Since the heights are given we can use the equation [latex]e = \sqrt{\frac{bounce height}{drop height}}[/latex] to solve for coefficient of restitution.

Solution

[latex]e = \sqrt{\frac{1.31}{1.83}} = 0.85[/latex]

Discussion

The coefficient of restitution of the basketball is 0.85. Note that the coefficient of restitution is specific to the two objects/surfaces. That is, e = 0.85 only applies to the basketball and court. Of course, if you bounced the basketball on another surface, such as grass, the coefficient of restitution would be much different.

Example: Calculating post-collision velocities

A professional golfer can swing the driver with a clubhead speed of 110 mph.

a) What is the velocity of a golf ball as it leaves the clubface?

b) what is the velocity of the clubhead after impact?

The mass of the driver and golf ball are 176 grams and 45 grams, respectively, and the coefficient of restitution is 0.79.

Strategy

In this case the pre-collision velocity of the golf ball is zero, and we can use the two equations above. We may also need to convert mph to m/s and grams to kg. We can set the golfball to be object 1 and the club to be object 2.

Solution a)

To convert mph to m/s we can first convert to km/hr by multiplying by 1.61 and then to m/s by dividing by 3.6:

[latex]100 \text{mph} / 1.61 = 161 \text{km/hr}  \text{and } 161\text{km/hr} / 3.6 = 44.7 \text{m/s}[/latex]

The post-collision velocity of the golf ball can be solved using:

[latex]v\prime_1 = \frac{m_1v\prime_1 + m_2v\prime_2 + e*m_2\left(v_2 - v_1\right)}{m_1 + m_2}[/latex], where

[latex]v\prime_1 = \frac{0.045 g * 0 m/s + 0.176 kg * 44.7 + 0.79*0.176\left(44.7 m/s - 0 m/s\right)}{0.045 kg + 0.176 kg}[/latex]

[latex]v\prime_1 = 63.7 m/s[/latex]

Solution b)

The velocity of the club can be determined using the second equation above (that includes e) or the original equation for conservation of momentum. Both will yield the same answer where:

[latex]v\prime_2 = 28.4 m/s[/latex]

Discussion

The golf ball has a post-collision velocity that is larger than the pre-collision velocity of the golf club. This is due to the golf ball having a lower mass than the club. Additionally, we can observe that the velocity of the club is reduced post-collision, but is still moving in the same direction. Note that these estimates apply only for the instant after the collision and do not account for the motion of the body or its effect on the club after the collision (i.e. during the follow-through).

 

 

Example: Calculating Final Velocity and Energy Release: Two Carts Collide

In the collision pictured in the previous example, two carts collide inelastically. Cart 1 (denoted [latex]{m}_{1}[/latex] carries a spring which is initially compressed. During the collision, the spring releases its potential energy and converts it to internal kinetic energy. The mass of cart 1 and the spring is 0.350 kg, and the cart and the spring together have an initial velocity of [latex]2\text{.}\text{00 m/s}[/latex]. Cart 2 (denoted [latex]{m}_{2}[/latex]) has a mass of 0.500 kg and an initial velocity of [latex]-0\text{.}\text{500 m/s}[/latex]. After the collision, cart 1 is observed to recoil with a velocity of [latex]-4\text{.}\text{00 m/s}[/latex].
(a) What is the final velocity of cart 2?
(b) How much energy was released by the spring (assuming all of it was converted into internal kinetic energy)?

Strategy

We can use conservation of momentum to find the final velocity of cart 2, because [latex]{F}_{\text{net}}=0[/latex] (the track is frictionless and the force of the spring is internal). Once this velocity is determined, we can compare the internal kinetic energy before and after the collision to see how much energy was released by the spring.

Solution for (a)

As before, the equation for conservation of momentum in a two-object system is

[latex]{m}_{1}{v}_{1}+{m}_{2}{v}_{2}={m}_{1}{v\prime }_{1}+{m}_{2}{v\prime }_{2}\text{.}[/latex]

The only unknown in this equation is [latex]{v\prime }_{2}[/latex]. Solving for [latex]{v\prime }_{2}[/latex] and substituting known values into the previous equation yields

[latex]\begin{array}{lll}{v\prime }_{2}& =& \frac{{m}_{1}{v}_{1}+{m}_{2}{v}_{2}-{m}_{1}{v\prime }_{1}}{{m}_{2}}\\ & =& \frac{\left(\text{0.350 kg}\right)\left(\text{2.00 m/s}\right)+\left(\text{0.500 kg}\right)\left(-\text{0.500 m/s}\right)}{\text{0.500 kg}}-\frac{\left(\text{0.350 kg}\right)\left(-\text{4.00 m/s}\right)}{\text{0.500 kg}}\\ & =& \text{3.70 m/s.}\end{array}[/latex]


Solution for (b)

The internal kinetic energy before the collision is

[latex]\begin{array}{lll}{\text{KE}}_{\text{int}}& =& \frac{1}{2}{m}_{1}{v}_{1}^{2}+\frac{1}{2}{m}_{2}{v}_{2}^{2}\\ & =& \frac{1}{2}\left(0\text{.}\text{350 kg}\right){\left(\text{2.00 m/s}\right)}^{2}+\frac{1}{2}\left(0\text{.}\text{500 kg}\right){\left(–0\text{.}\text{500 m/s}\right)}^{2}\\ & =& 0\text{.}\text{763 J}.\end{array}[/latex]

After the collision, the internal kinetic energy is

[latex]\begin{array}{lll}{\text{KE}\prime }_{\text{int}}& =& \frac{1}{2}{m}_{1}{v\prime }_{1}^{2}+\frac{1}{2}{m}_{2}{v\prime }_{2}^{2}\\ & =& \frac{1}{2}\left(\text{0.350 kg}\right){\left(-\text{4.00 m/s}\right)}^{2}+\frac{1}{2}\left(\text{0.500 kg}\right){\left(\text{3.70 m/s}\right)}^{2}\\ & =& \text{6.22 J.}\end{array}[/latex]

The change in internal kinetic energy is thus

[latex]\begin{array}{lll}{KE\prime }_{\text{int}}-{\text{KE}}_{\text{int}}& =& \text{6.22 J}-0\text{.}\text{763 J}\\ & =& \text{5.46 J.}\end{array}[/latex]


Discussion

The final velocity of cart 2 is large and positive, meaning that it is moving to the right after the collision. The internal kinetic energy in this collision increases by 5.46 J. That energy was released by the spring.

License

Icon for the Creative Commons Attribution 4.0 International License

Introduction to Biomechanics Copyright © 2022 by Rob Pryce is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book