Chapter 5: Work, Power, and Energy

Problems & Exercises

5.1 Work

  1. How much work does a supermarket checkout attendant do on a can of soup he pushes 0.600 m horizontally with a force of 5.00 N? Express your answer in joules and kilocalories.
    Solution: [latex]3\text{.}\text{00}\text{ J}=7\text{.}\text{17}×{\text{10}}^{-4}\text{ kcal}[/latex]
  2. A 75.0-kg person climbs stairs, gaining 2.50 meters in height. Find the work done to accomplish this task.
  3. (a) Calculate the work done on a 1500-kg elevator car by its cable to lift it 40.0 m at constant speed, assuming friction averages 100 N.
    (b) What is the work done on the lift by the gravitational force in this process?
    (c) What is the total work done on the lift?
    Solution: (a) [latex]5\text{.}\text{92}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex]; (b) [latex]-5\text{.}\text{88}×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex]; (c) The net force is zero.
  4. Calculate the work done by an 85.0-kg man who pushes a crate 4.00 m up along a ramp that makes an angle of [latex]\text{20}\text{.}0\text{º}[/latex] with the horizontal. (See figure below) He exerts a force of 500 N on the crate parallel to the ramp and moves at a constant speed. Be certain to include the work he does on the crate and on his body to get up the ramp.

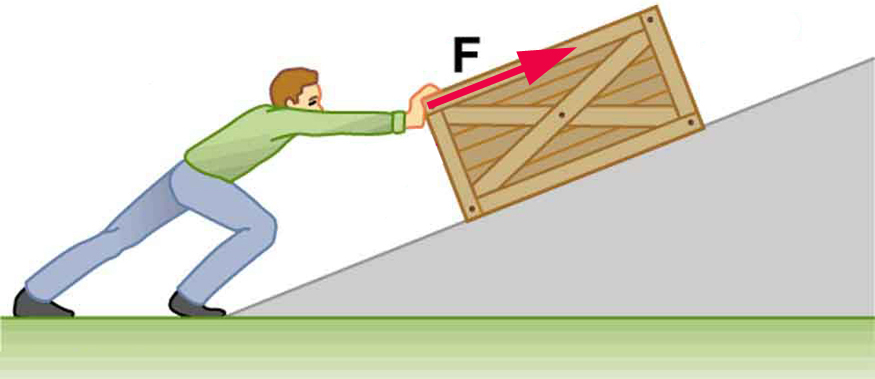
    A person is pushing a heavy crate up a ramp. The force vector F applied by the person is acting parallel to the ramp.
    A man pushes a crate up a ramp.

    Solution: [latex]3\text{.}\text{14}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex]

  5. How much work is done by the boy pulling his sister 30.0 m in a wagon as shown in the figure below? Assume no friction acts on the wagon.
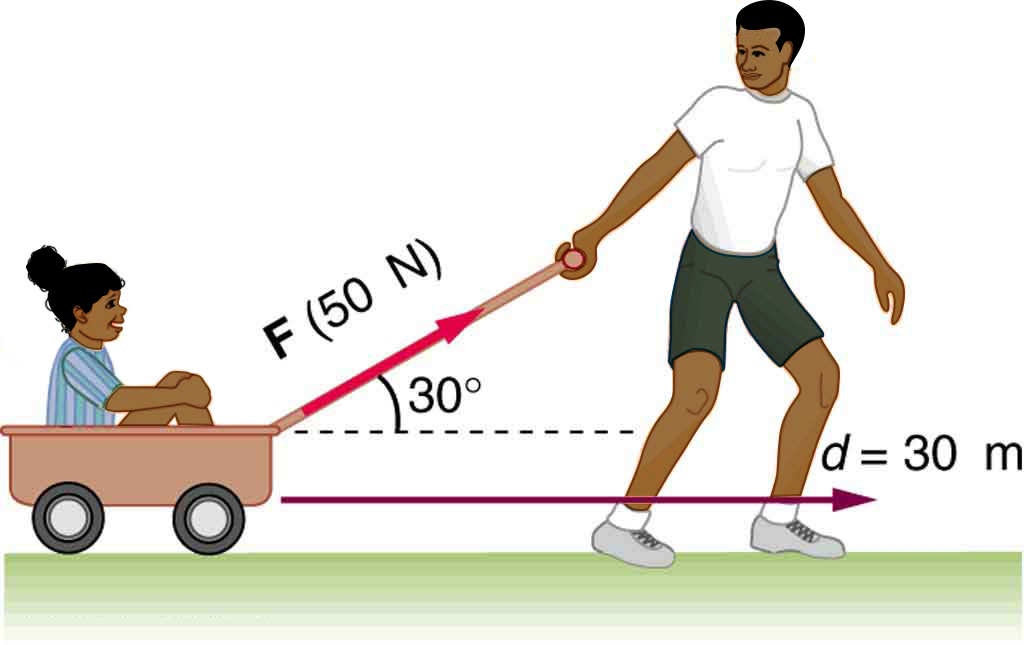
    A child is sitting inside a wagon and being pulled by a boy with a force F at an angle thirty degrees upward from the horizontal. F is equal to fifty newtons, the displacement vector d is horizontal in the direction of motion. The magnitude of d is thirty meters.
    The boy does work on the system of the wagon and the child when he pulls them as shown.
  6. A shopper pushes a grocery cart 20.0 m at constant speed on level ground, against a 35.0 N frictional force. He pushes in a direction [latex]\text{25}\text{.}0\text{º}[/latex] below the horizontal.
    (a) What is the work done on the cart by friction?
    (b) What is the work done on the cart by the gravitational force?
    (c) What is the work done on the cart by the shopper?
    (d) Find the force the shopper exerts, using energy considerations.
    (e) What is the total work done on the cart?
    Solution: (a) [latex]-\text{700}\phantom{\rule{0.25em}{0ex}}\text{J}[/latex]; (b) 0; (c) 700 J; (d) 38.6 N; (e) 0
  7. Suppose the ski patrol lowers a rescue sled and victim, having a total mass of 90.0 kg, down a [latex]\text{60}\text{.}0\text{º}[/latex] slope at constant speed, as shown in the figure below. The coefficient of friction between the sled and the snow is 0.100.
    (a) How much work is done by friction as the sled moves 30.0 m along the hill?
    (b) How much work is done by the rope on the sled in this distance?
    (c) What is the work done by the gravitational force on the sled?
    (d) What is the total work done?

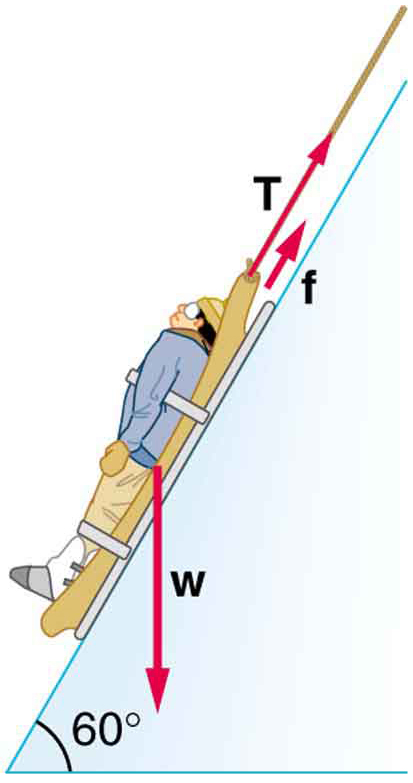
    A person on a rescue sled is shown being pulled up a slope. The slope makes an angle of sixty degrees from the horizontal. The weight of the person is shown by vector w acting vertically downward. The tension in the rope depicted by vector T is along the incline in the upward direction; vector f depicting frictional force is also acting in the same direction.
    A rescue sled and victim are lowered down a steep slope.
  8. *A constant 20-N force pushes a small ball in the direction of the force over a distance of 5.0 m. What is the work done by the force?
  9. *A toy cart is pulled a distance of 6.0 m in a straight line across the floor. The force pulling the cart has a magnitude of 20 N and is directed at 37°37° above the horizontal. What is the work done by this force?
  10. *A 5.0-kg box rests on a horizontal surface. The coefficient of kinetic friction between the box and surface is μK=0.50. A horizontal force pulls the box at constant velocity for 10 cm. Find the work done by
    (a) the applied horizontal force
    (b) the frictional force, and
    (c) the net force
    Solution: (a) 2.45 J; (b) – 2.45 J; (c) 0 J
  11. *A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (μk=0.20)(μk=0.20) at constant velocity by a force directed 25°25° above the horizontal. Calculate
    (a) the work of the applied force
    (b) the work of friction, and
    (c) the total work
  12. *Suppose that the sled plus passenger of the preceding problem is pushed 20 m across the snow at constant velocity by a force directed 30°30° below the horizontal. Calculate
    (a) the work of the applied force
    (b) the work of friction, and
    (c) the total work
    Solution: (a) 2.22 kJ; (b) −2.22 kJ; (c) 0 J
  13. *A bungee cord is essentially a very long rubber band that can stretch up to four times its unstretched length. However, its spring constant varies over its stretch [see Menz, P.G. “The Physics of Bungee Jumping.” The Physics Teacher (November 1993) 31: 483-487]. Take the length of the cord to be along the x-direction and define the stretch x as the length of the cord lminus its un-stretched length l0; that is, x=l−l0 (see below). Suppose a particular bungee cord has a spring constant, for 0≤x≤4.88m, of k1=204N/m and for 4.88m≤x, of k2=111N/m. (Recall that the spring constant is the slope of the force F(x) versus its stretch x.)
    (a) What is the tension in the cord when the stretch is 16.7 m (the maximum desired for a given jump)?
    (b) How much work must be done against the elastic force of the bungee cord to stretch it 16.7 m?

    A photograph of a person bungee jumping from a bridge above a river is accompanied by an illustration of the situation. The illustration shows the jumper at the his lowest position, and the bungee stretched by a distance l minus l sub zero.
    (credit: modification of work by Graeme Churchard)

5.2 Kinetic Energy and the Work-Energy Theorem

  1. Compare the kinetic energy of a 20,000-kg truck moving at 110 km/h with that of an 80.0-kg astronaut in orbit moving at 27,500 km/h.
    Solution: [latex]1/\text{250}[/latex]
  2. (a) How fast must a 3000-kg elephant move to have the same kinetic energy as a 65.0-kg sprinter running at 10.0 m/s?
    (b) Discuss how the larger energies needed for the movement of larger animals would relate to metabolic rates.
  3. Confirm the value given for the kinetic energy of an aircraft carrier in the Energy of Various Objects and Phenomena table in Section 5.6. You will need to look up the definition of a nautical mile (1 knot = 1 nautical mile/h).
    Solution: [latex]    1\text{.}1×{\text{10}}^{\text{10}}\phantom{\rule{0.20em}{0ex}}\text{J}[/latex]
  4. Boxing gloves are padded to lessen the force of a blow.
    (a) Calculate the force exerted by a boxing glove on an opponent’s face, if the glove and face compress 7.50 cm during a blow in which the 7.00-kg arm and glove are brought to rest from an initial speed of 10.0 m/s.
    (b) Calculate the force exerted by an identical blow in the days when no gloves were used and the knuckles and face would compress only 2.00 cm.
    (c) Discuss the magnitude of the force with glove on. Does it seem high enough to cause damage even though it is lower than the force with no glove?
  5. Using energy considerations, calculate the average force a 60.0-kg sprinter exerts backward on the track to accelerate from 2.00 to 8.00 m/s in a distance of 25.0 m, if he encounters a headwind that exerts an average force of 30.0 N against him.
    Solution: 102 N
  6. *Calculate the kinetic energy of an 80.-kg runner sprinting at 10. m/s
    Solution: 4.0 kJ
  7. *A 5.0-kg body has three times the kinetic energy of an 8.0-kg body. Calculate the ratio of the speeds of these bodies.
  8. *A sled starts from rest at the top of a snow-covered incline that makes a 22° angle with the horizontal. After sliding 75 m down the slope, its speed is 14 m/s. Use the work-energy theorem to calculate the coefficient of kinetic friction between the runners of the sled and the snowy surface.

5.3 Gravitational Potential Energy

  1. (a) How much gravitational potential energy (relative to the ground on which it is built) is stored in the Great Pyramid of Cheops, given that its mass is about [latex]7\mathrm{ × }{\text{10}}^{9}\text{ kg}[/latex] and its center of mass is 36.5 m above the surrounding ground?
    (b) How does this energy compare with the daily food intake of a person?
  2. Suppose a 350-g kookaburra (a large kingfisher bird) picks up a 75-g snake and raises it 2.5 m from the ground to a branch.
    (a) How much work did the bird do on the snake?
    (b) How much work did it do to raise its own center of mass to the branch?
    Solution: (a) 1.8 J; (b) 8.6 J
  3. In a downhill ski race, surprisingly, little advantage is gained by getting a running start. (This is because the initial kinetic energy is small compared with the gain in gravitational potential energy on even small hills.) To demonstrate this, find the final speed and the time taken for a skier who skies 70.0 m along a [latex]\text{30º}[/latex] slope neglecting friction:
    (a) Starting from rest.
    (b) Starting with an initial speed of 2.50 m/s.
    (c) Does the answer surprise you? Discuss why it is still advantageous to get a running start in very competitive events.

5.4 Conservative Forces and Potential Energy

  1. A [latex]5\text{.}\text{00}×{\text{10}}^{5}\text{-kg}[/latex] subway train is brought to a stop from a speed of 0.500 m/s in 0.400 m by a large spring bumper at the end of its track. What is the force constant [latex]k[/latex] of the spring?
    Solution: [latex]\text{7.81}×{\text{10}}^{5}\phantom{\rule{0.20em}{0ex}}\text{N/m}[/latex]
  2. A pogo stick has a spring with a force constant of [latex]2\text{.}\text{50}×{\text{10}}^{4}\phantom{\rule{0.20em}{0ex}}\text{N/m}[/latex], which can be compressed 12.0 cm. To what maximum height can a child jump on the stick using only the energy in the spring, if the child and stick have a total mass of 40.0 kg?
  3. *In the cartoon movie Pocahontas, Pocahontas runs to the edge of a cliff and jumps off, showcasing the fun side of her personality.
    (a) If she is running at 3.0 m/s before jumping off the cliff and she hits the water at the bottom of the cliff at 20.0 m/s, how high is the cliff? Assume negligible air drag in this cartoon.
    (b) If she jumped off the same cliff from a standstill, how fast would she be falling right before she hit the water?
  4. *In the reality television show “Amazing Race”, a contestant is firing 12-kg watermelons from a slingshot to hit targets down the field. The slingshot is pulled back 1.5 m and the watermelon is considered to be at ground level. The launch point is 0.3 m from the ground and the targets are 10 m horizontally away. Calculate the spring constant of the slingshot.
    Solution: 8700 N/m 

5.5 Nonconservative Forces

  1. A 60.0-kg skier with an initial speed of 12.0 m/s coasts up a 2.50-m-high rise as shown in the figure below. Find her final speed at the top, given that the coefficient of friction between her skis and the snow is 0.0800. (Hint: Find the distance traveled up the incline assuming a straight-line path as shown in the figure.)
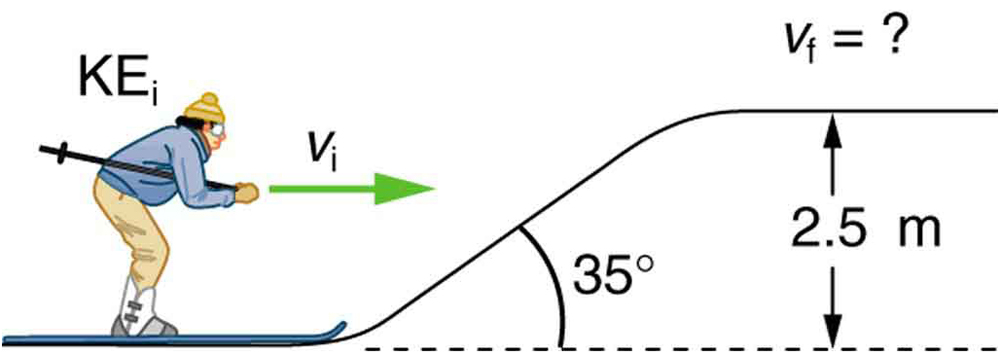
    A skier is about to go up an inclined slope with some initial speed v sub i shown by an arrow towards right. The slope makes a thirty-five-degree with the horizontal. The height of the point where the slope ends from the skiers’ starting position is two point five meters. Final speed of the skier at the end of the inclined slope is unknown.
    The skier’s initial kinetic energy is partially used in coasting to the top of a rise.

    Solution: 9.46 m/s

  2. (a) How high a hill can a car coast up (engine disengaged) if work done by friction is negligible and its initial speed is 110 km/h?
    (b) If, in actuality, a 750-kg car with an initial speed of 110 km/h is observed to coast up a hill to a height 22.0 m above its starting point, how much thermal energy was generated by friction?
    (c) What is the average force of friction if the hill has a slope [latex]2\text{.}5º[/latex] above the horizontal?

5.6 Conservation of Energy

  1. *A boy throws a ball of mass 0.25 kg straight upward with an initial speed of 20 m/s. When the ball returns to the boy, its speed is 17m/s. How much much work does air resistance do on the ball during its flight?
    Solution: 14 J
  2. *A 1.0-kg ball at the end of a 2.0-m string swings in a vertical plane. At its lowest point the ball is moving with a speed of 10 m/s.
    (a) What is its speed at the top of its path?
    (b) What is the tension in the string when the ball is at the bottom and at the top of its path?
  3. *Ignoring details associated with friction, extra forces exerted by arm and leg muscles, and other factors, we can consider a pole vault as the conversion of an athlete’s running kinetic energy to gravitational potential energy. If an athlete is to lift his body 4.8 m during a vault, what speed must he have when he plants his pole?
    Solution: 9.7m/s
  4. *Tarzan grabs a vine hanging vertically from a tall tree when he is running ant 9.0 m/s.
    (a) How high can he swing upward?
    (b) Does the length of the vine affect this height?
  5. *Assume that the force of a bow on an arrow behaves like the spring force. In aiming the arrow, an archer pulls the bow back 50 cm and holds it in position with a force of 150N. If the mass of the arrow is 50g and the “spring” is massless, what is the speed of the arrow immediately after it leaves the bow?
    Solution: 39m/s
  6. *A 100−kg man is skiing across level ground at a speed of 8.0m/s when he comes to the small slope 1.8 m higher than ground level shown in the following figure.
    (a) If the skier coasts up the hill, what is his speed when he reaches the top plateau? Assume friction between the snow and skis is negligible.
    (b) What is his speed when he reaches the upper level if an     80−N frictional force acts on the skis?
    The figure is a drawing of a skier who has gone up a slope that is 8.0 meters long. The vertical distance between the top of the slope and its bottom is 1.8 meters.
  7. *A sled of mass 70kg starts from rest and slides down a 10° incline that is 80m long. It then travels for 20m horizontally before starting back up an 8° incline. it travels 80m this incline before coming to rest. what is the magnitude of the net work done on the sled by friction? 
    Solution: 1900 J
  8. *A girl on a skateboard (total mass of 40 kg) is moving at a speed of 10 m/s at the bottom of a long ramp. The ramp is inclined at 20° with respect to the horizontal. If she travels 14.2 m upward along the ramp before stopping, what is the net frictional force on her?
  9. *A baseball of mass 0.25 kg is hit at home plate with a speed of 40 m/s. When it lands in a seat in the left-field bleachers a horizontal distance 120 m from home plate, it is moving at 30 m/s. If the ball lands 20 m above the spot where it was hit, how much work is done on it by air resistance?
    Solution: –39 J

5.7 Power

  1. A person in good physical condition can put out 100 W of useful power for several hours at a stretch, perhaps by pedaling a mechanism that drives an electric generator. Neglecting any problems of generator efficiency and practical considerations such as resting time:
    (a) How many people would it take to run a 4.00-kW electric clothes dryer?
    (b) How many people would it take to replace a large electric power plant that generates 800 MW?
    Solution: (a) 40; (b) 8 million
  2. (a) What is the average useful power output of a person who does [latex]6\text{.}\text{00}×{\text{10}}^{6}\phantom{\rule{0.20em}{0ex}}\text{J}[/latex] of useful work in 8.00 h?
    (b) Working at this rate, how long will it take this person to lift 2000 kg of bricks 1.50 m to a platform? (Work done to lift his body can be omitted because it is not considered useful output here.)
    Solution: (a) [latex]\text{208 W}[/latex]; (b) 141 s
  3. *A man of mass 80 kg runs up a flight of stairs 20 m high in 10 s.
    (a) how much power is used to lift the man?
    (b) If the man’s body is 25% efficient, how much power does he expend?
    Solution: (a) 1.57 kW; (b) 6.28 kW
  4. *The man of the preceding problem consumes approximately 1.05×107J (2500 food calories) of energy per day in maintaining a constant weight. What is the average power he produces over a day? Compare this with his power production when he runs up the stairs.
  5. *A girl pulls her 15-kg wagon along a flat sidewalk by applying a 10-N force at 37° to the horizontal. Assume that friction is negligible and that the wagon starts from rest.
    (a) How much work does the girl do on the wagon in the first 2.0 s.
    (b) How much instantaneous power does she exert at t=2.0s?
    Solution: (a) 8.51 J; (b) 8.51 W
  6. *When jogging at 13 km/h on a level surface, a 70-kg man uses energy at a rate of approximately 850 W. Using the facts that the “human engine” is approximately 25% efficient, determine the rate at which this man uses energy when jogging up a 5.0° slope at this same speed. Assume that the frictional retarding force is the same in both cases.
    Solution: 1.7 kW

5.8 Work, Power & Energy in Humans

  1. (a) How long can you rapidly climb stairs (116/min) on the 93.0 kcal of energy in a 10.0-g pat of butter?
    (b) How many flights is this if each flight has 16 stairs?
    Solution: (a) 9.5 min; (b) 69 flights of stairs
  2. (a) What is the power output in watts and horsepower of a 70.0-kg sprinter who accelerates from rest to 10.0 m/s in 3.00 s?
    (b) Considering the amount of power generated, do you think a well-trained athlete could do this repetitively for long periods of time?
  3. Calculate the power output in watts and horsepower of a shot-putter who takes 1.20 s to accelerate the 7.27-kg shot from rest to 14.0 m/s, while raising it 0.800 m. (Do not include the power produced to accelerate his body.)
    A close view of a shot-putter throwing the shot.
    Shot putter at the Dornoch Highland Gathering in 2007. (credit: John Haslam, Flickr)

    Solution: 641 W, 0.860 hp

  4. (a) What is the efficiency of an out-of-condition professor who does [latex]2\text{.}\text{10}×{\text{10}}^{5}\text{ J}[/latex] of useful work while metabolizing 500 kcal of food energy? (b) How many food calories would a well-conditioned athlete metabolize in doing the same work with an efficiency of 20%?
  5. Energy that is not utilized for work or heat transfer is converted to the chemical energy of body fat containing about 39 kJ/g. How many grams of fat will you gain if you eat 10,000 kJ (about 2500 kcal) one day and do nothing but sit relaxed for 16.0 h and sleep for the other 8.00 h? Use data from the Energy and Oxygen Consumption Rates (Power) table in Section 5.8 for the energy consumption rates of these activities.
    Solution: 31 g
  6. Using data from the Energy and Oxygen Consumption Rates (Power) table in Section 5.8, calculate the daily energy needs of a person who sleeps for 7.00 h, walks for 2.00 h, attends classes for 4.00 h, cycles for 2.00 h, sits relaxed for 3.00 h, and studies for 6.00 h. (Studying consumes energy at the same rate as sitting in class.)
  7. What is the efficiency of a subject on a treadmill who puts out work at the rate of 100 W while consuming oxygen at the rate of 2.00 L/min? (Hint: See the Energy and Oxygen Consumption Rates (Power) table in Section 5.8)
    Solution: 14.3%
  8. Shoveling snow can be extremely taxing because the arms have such a low efficiency in this activity. Suppose a person shoveling a footpath metabolizes food at the rate of 800 W.
    (a) What is her useful power output?
    (b) How long will it take her to lift 3000 kg of snow 1.20 m? (This could be the amount of heavy snow on 20 m of footpath.)
    (c) How much waste heat transfer in kilojoules will she generate in the process?
  9. Very large forces are produced in joints when a person jumps from some height to the ground.
    (a) Calculate the magnitude of the force produced if an 80.0-kg person jumps from a 0.600–m-high ledge and lands stiffly, compressing joint material 1.50 cm as a result. (Be certain to include the weight of the person.)
    (b) In practice the knees bend almost involuntarily to help extend the distance over which you stop. Calculate the magnitude of the force produced if the stopping distance is 0.300 m.
    (c) Compare both forces with the weight of the person.
    Solution: (a) [latex]3\text{.}\text{21}×{\text{10}}^{4}\text{ N}[/latex]; (b) [latex]2\text{.}\text{35}×{\text{10}}^{3}\text{ N}[/latex]; (c) Ratio of net force to weight of person is 41.0 in part (a); 3.00 in part (b)
  10. Jogging on hard surfaces with insufficiently padded shoes produces large forces in the feet and legs.
    (a) Calculate the magnitude of the force needed to stop the downward motion of a jogger’s leg, if his leg has a mass of 13.0 kg, a speed of 6.00 m/s, and stops in a distance of 1.50 cm. (Be certain to include the weight of the 75.0-kg jogger’s body.)
    (b) Compare this force with the weight of the jogger.
  11. (a) Calculate the energy in kJ used by a 55.0-kg woman who does 50 deep knee bends in which her center of mass is lowered and raised 0.400 m. (She does work in both directions.) You may assume her efficiency is 20%.
    (b) What is the average power consumption rate in watts if she does this in 3.00 min?
    Solution: (a) 108 kJ; (b) 599 W
  12. Kanellos Kanellopoulos flew 119 km from Crete to Santorini, Greece, on April 23, 1988, in the Daedalus 88, an aircraft powered by a bicycle-type drive mechanism (see figure below). His useful power output for the 234-min trip was about 350 W. Using the efficiency for cycling from the Efficiency of the Human Body and Mechanical Devices table in Section 5.6, calculate the food energy in kilojoules he metabolized during the flight.
    An aircraft flying in the air shown from outside, which is powered by a bicycle-type drive mechanism.
    The Daedalus 88 in flight. (credit: NASA photo by Beasley)

     

  13. The swimmer shown in the figure below exerts an average horizontal backward force of 80.0 N with his arm during each 1.80 m long stroke.
    (a) What is his work output in each stroke?
    (b) Calculate the power output of his arms if he does 120 strokes per minute.
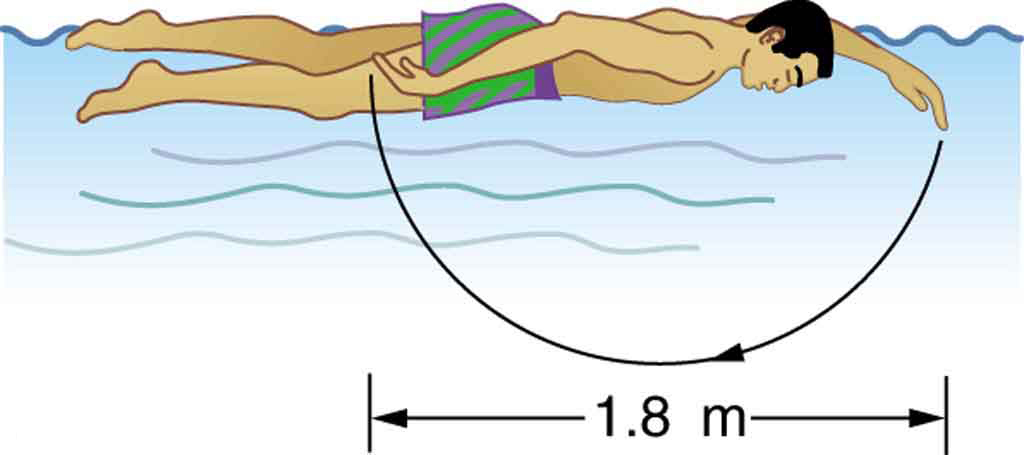
    A person swimming and his arm motion in each stroke is represented. The arm action is shown by an arc starting from where his hand enters the surface of the water and ending at the point where his hand emerges from the water. The diameter of this arc made by the person’s hand tip in one stroke is one point eight meters.
    Solution: (a) 144 J; (b) 288 W
  14. Mountain climbers carry bottled oxygen when at very high altitudes.
    (a) Assuming that a mountain climber uses oxygen at twice the rate for climbing 116 stairs per minute (because of low air temperature and winds), calculate how many liters of oxygen a climber would need for 10.0 h of climbing. (These are liters at sea level.) Note that only 40% of the inhaled oxygen is utilized; the rest is exhaled.
    (b) How much useful work does the climber do if he and his equipment have a mass of 90.0 kg and he gains 1000 m of altitude?
    (c) What is his efficiency for the 10.0-h climb?
  15. The awe-inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high, with a mass of about [latex]7×{10}^{9}\phantom{\rule{0.25em}{0ex}}\text{kg}[/latex]. (The pyramid’s dimensions are slightly different today due to quarrying and some sagging.) Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year.
    (a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height.
    (b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps (see figure below), bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 kcal/h. What does your answer imply about how much of their work went into block-lifting, versus how much work went into friction and lifting and lowering their own bodies?
    (c) Calculate the mass of food that had to be supplied each day, assuming that the average worker required 3600 kcal per day and that their diet was 5% protein, 60% carbohydrate, and 35% fat. (These proportions neglect the mass of bulk and nondigestible materials consumed.)

    A model of a step pyramid is shown with ramps along the sides of each step.
    Ancient pyramids were probably constructed using ramps as simple machines. (credit: Franck Monnier, Wikimedia Commons)

    Solution: (a) [latex]2\text{.}\text{50}×{\text{10}}^{\text{12}}\text{ J}[/latex]; (b) 2.52%; (c) [latex]1\text{.}4×{\text{10}}^{4 }\text{kg}[/latex] (14 metric tons)

  16. (a) How long can you play tennis on the 800 kJ (about 200 kcal) of energy in a candy bar?
    (b) Does this seem like a long time? Discuss why exercise is necessary but may not be sufficient to cause a person to lose weight.

Additional Problems

  1. *A hockey puck of mass 0.17 kg is shot across a rough floor with the roughness different at different places, which can be described by a position-dependent coefficient of kinetic friction. For a puck moving along the x-axis, the coefficient of kinetic friction is the following function of x, where x is in m: μ(x)=0.1+0.05x. Find the work done by the kinetic frictional force on the hockey puck when it has moved
    (a) from x=0 to x=2m, and
    (b) from x=2m to x=4m
    Solution: (a) −0.5N⋅m; (b) −0.83N⋅m
  2. *A horizontal force of 20 N is required to keep a 5.0 kg box traveling at a constant speed up a frictionless incline for a vertical height change of 3.0 m.
    (a) What is the work done by gravity during this change in height?
    (b) What is the work done by the normal force?
    (c) What is the work done by the horizontal force?
  3. *A 7.0-kg box slides along a horizontal frictionless floor at 1.7 m/s and collides with a relatively massless spring that compresses 23 cm before the box comes to a stop.
    (a) How much kinetic energy does the box have before it collides with the spring?
    (b) Calculate the work done by the spring.
    (c) Determine the spring constant of the spring.
    Solution: (a) 10. J; (b) –10. J; (c) 380 N/m
  4. *You are driving your car on a straight road with a coefficient of friction between the tires and the road of 0.55. A large piece of debris falls in front of your view and you immediate slam on the brakes, leaving a skid mark of 30.5 m (100-feet) long before coming to a stop. A policeman sees your car stopped on the road, looks at the skid mark, and gives you a ticket for traveling over the 13.4 m/s (30 mph) speed limit. Should you fight the speeding ticket in court?
  5. *A crate is being pushed across a rough floor surface. If no force is applied on the crate, the crate will slow down and come to a stop. If the crate of mass 50 kg moving at speed 8 m/s comes to rest in 10 seconds, what is the rate at which the frictional force on the crate takes energy away from the crate?
    Solution: 160 J/s
  6. *Suppose a horizontal force of 20 N is required to maintain a speed of 8 m/s of a 50 kg crate.
    (a) What is the power of this force?
    (b) Note that the acceleration of the crate is zero despite the fact that 20 N force acts on the crate horizontally. What happens to the energy given to the crate as a result of the work done by this 20 N force?
  7. *A cyclist in a race must climb a 5° hill at a speed of 8 m/s. If the mass of the bike and the biker together is 80 kg, what must be the power output of the biker to achieve the goal?
  8. *A boy pulls a 5-kg cart with a 20-N force at an angle of 30° above the horizontal for a length of time. Over this time frame, the cart moves a distance of 12 m on the horizontal floor.
    (a) Find the work done on the cart by the boy.
    (b) What will be the work done by the boy if he pulled with the same force horizontally instead of at an angle of 30° above the horizontal over the same distance?
    Solution: (a) 208N⋅m; (b) 240N⋅m
  9. *In the Hunger Games movie, Katniss Everdeen fires a 0.0200-kg arrow from ground level to pierce an apple up on a stage. The spring constant of the bow is 330 N/m and she pulls the arrow back a distance of 0.55 m. The apple on the stage is 5.00 m higher than the launching point of the arrow. At what speed does the arrow
    (a) leave the bow?
    (b) strike the apple?
    Solution: (a) 70.6 m/s; (b) 69.9 m/s
  10. *In a “Top Fail” video, two women run at each other and collide by hitting exercise balls together. If each woman has a mass of 50 kg, which includes the exercise ball, and one woman runs to the right at 2.0 m/s and the other is running toward her at 1.0 m/s,
    (a) how much total kinetic energy is there in the system?
    (b) If energy is conserved after the collision and each exercise ball has a mass of 2.0 kg, how fast would the balls fly off toward the camera?
  11. *In an iconic movie scene, Forrest Gump runs around the country. If he is running at a constant speed of 3 m/s, would it take him more or less energy to run uphill or downhill and why?
  12. *A child (32 kg) jumps up and down on a trampoline. The trampoline exerts a spring restoring force on the child with a constant of 5000 N/m. At the highest point of the bounce, the child is 1.0 m above the level surface of the trampoline. What is the compression distance of the trampoline? Neglect the bending of the legs or any transfer of energy of the child into the trampoline while jumping.
    Solution: 42 cm
  13. *A skier starts from rest and slides downhill. What will be the speed of the skier if he drops by 20 meters in vertical height? Ignore any air resistance (which will, in reality, be quite a lot), and any friction between the skis and the snow.
  14. *A 300 g hockey puck is shot across an ice-covered pond. Before the hockey puck was hit, the puck was at rest. After the hit, the puck has a speed of 40 m/s. The puck comes to rest after going a distance of 30 m.
    (a) Describe how the energy of the puck changes over time, giving the numerical values of any work or energy involved.
    (b) Find the magnitude of the net friction force.
    Solution: (a) Loss of energy is 240N⋅m; (b) F=8N
  15. *A projectile of mass 2 kg is fired with a speed of 20 m/s at an angle of 30° with respect to the horizontal.
    (a) Calculate the initial total energy of the projectile given that the reference point of zero gravitational potential energy at the launch position.
    (b) Calculate the kinetic energy at the highest vertical position of the projectile.
    (c)Calculate the gravitational potential energy at the highest vertical position.
    (d) Calculate the maximum height that the projectile reaches. Compare this result by solving the same problem using your knowledge of projectile motion.

 

License

Icon for the Creative Commons Attribution 4.0 International License

Introduction to Biomechanics Copyright © 2022 by Rob Pryce is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book