5.1 Work: The Scientific Definition

What It Means to Do Work

The scientific definition of work differs in some ways from its everyday meaning. Certain things we think of as hard work, such as writing an exam or carrying a heavy load on level ground, are not work as defined by a biomechanist. The scientific definition of work reveals its relationship to energy—whenever work is done, energy is transferred.

For work, in the scientific sense, to be done, a force must be exerted and there must be displacement in the direction of the force.

Formally, the work done on a system by a constant force is defined to be the product of force times distance. More specifically, it is the product of the component of the force in the direction of motion times distance through which the force acts. For one-way motion in one dimension, this is expressed in equation form as

where [latex]W[/latex] is work and [latex]\mathbf{d}[/latex] is the displacement of the system.

Similar to other equations involving force, if the force is not acting in exactly the same direction of motion (collinear), then we can determine the component of the force that acts in direction of motion (as [latex]Fx = \mathbf{F}*\text{cos}\theta, where [latex]\theta[/latex] is the angle between the force vector [latex]\mathbf{F}[/latex] and the displacement vector [latex]\mathbf{d}[/latex], as in the figure below).

So, we combine the above formulas and write work as:

To find the work done on a system that undergoes motion that is not one-way or that is in two or three dimensions, we divide the motion into one-way one-dimensional segments and add up the work done over each segment.

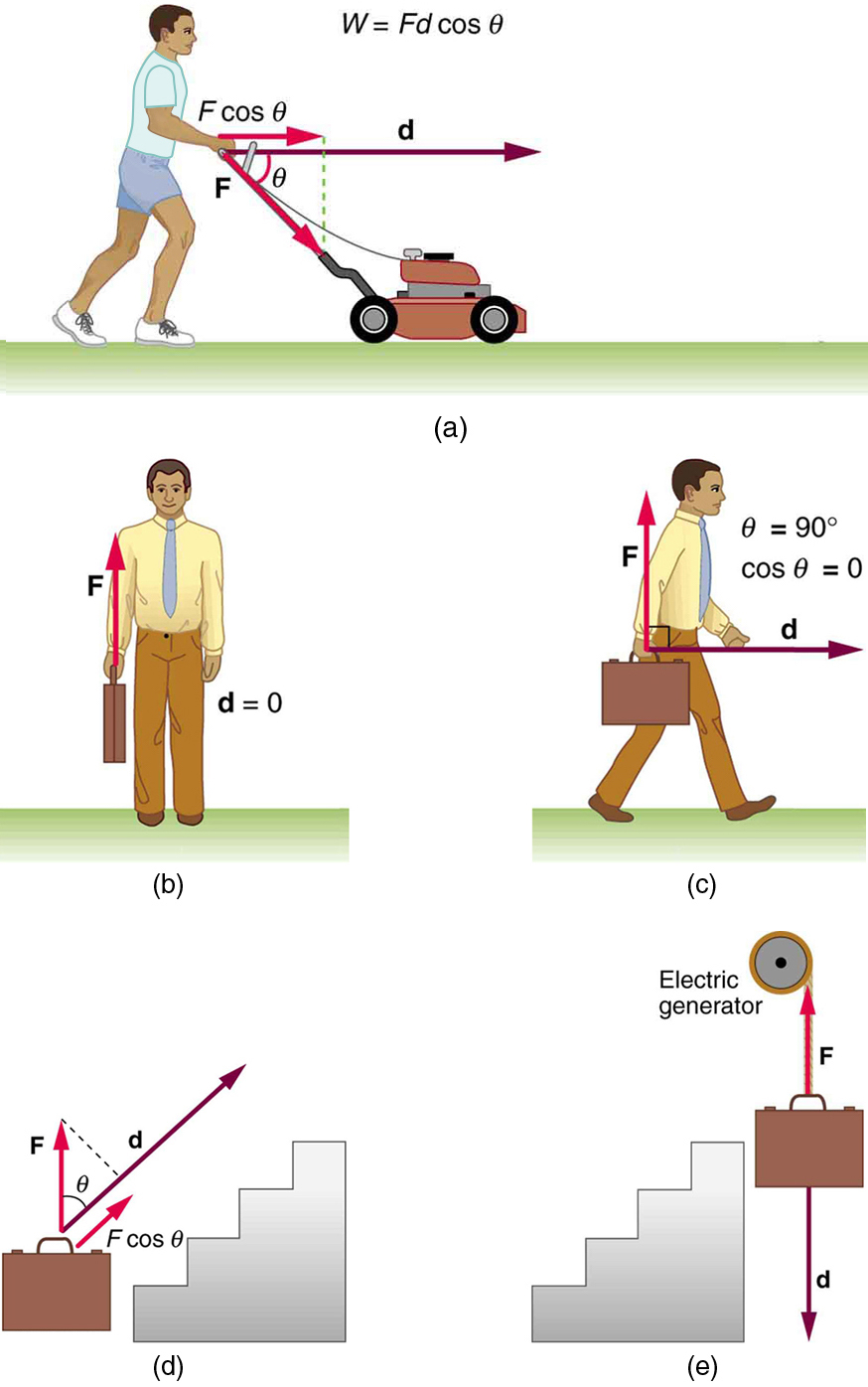
To examine what the definition of work means, let us consider the other situations shown in the figure above. The person holding the briefcase in Figure 7.2 (b) above does no work, for example. Here [latex]d=0[/latex], so [latex]W=0[/latex]. Why is it you get tired just holding a load? The answer is that your muscles are doing work against one another, but they are doing no work on the system of interest (the “briefcase-Earth system”). There must be displacement for work to be done, and there must be a component of the force in the direction of the motion. For example, the person carrying the briefcase on level ground in figure (c) above does no work on it, because the force is perpendicular to the motion. That is, [latex]\text{cos}\phantom{\rule{0.25em}{0ex}}\text{90}\text{º =}\phantom{\rule{0.25em}{0ex}}0[/latex], and so [latex]W=0[/latex].

In contrast, when a force exerted on the system has a component in the direction of motion, such as in figure (d) above, work is done—energy is transferred to the briefcase. Finally, in figure (e) above, energy is transferred from the briefcase to a generator. There are two good ways to interpret this energy transfer. One interpretation is that the briefcase’s weight does work on the generator, giving it energy. The other interpretation is that the generator does negative work on the briefcase, thus removing energy from it. The drawing shows the latter, with the force from the generator upward on the briefcase, and the displacement downward. This makes [latex]\theta =\text{180}\text{º}[/latex], and [latex]\text{cos 180}\text{º}=–1[/latex]; therefore, [latex]W[/latex] is negative.

Calculating Work

Work and energy have the same units. From the definition of work, we see that those units are force times distance. Thus, in SI units, work and energy are measured in newton-meters. A newton-meter is given the special name joule (J), and [latex]1\phantom{\rule{0.25em}{0ex}}\text{J}=1\phantom{\rule{0.25em}{0ex}}\text{N}\cdot \text{m}=1\phantom{\rule{0.25em}{0ex}}\text{kg}\cdot {\text{m}}^{2}{\text{/s}}^{2}[/latex]. One joule is not a large amount of energy; it would lift a small 100-gram apple a distance of about 1 meter.

Another unit of energy you may have encountered is the calorie. One calorie (1 cal) of heat is the amount of energy required to warm 1 g of water by [latex]1\text{º}\text{C}[/latex], and is equal to [latex]4.186\phantom{\rule{0.25em}{0ex}}\text{J}[/latex]. In the field of nutrition, we use calories to represent the amount of energy in foods, however in those cases we use the units kilocalories (kcal), which is equal to 1000 calories (from above). Therefore 1 kcal = 4186 J. Sometimes we'll use the term "Calorie" (with a capital 'C') to refer to the calories in food (which is actually 1 kcal, or 1000 'small c' calories).