Chapter 4: Linear Kinetics, Force and Newton’s Laws of Motion
Problems and Exercises
- *Two teenagers are pulling on ropes attached to a tree. The angle between the ropes is 30.0°. David pulls with a force of 400.0 N and Stephanie pulls with a force of 300.0 N.
(a) Find the magnitude of the resultant (net) force on the tree and the angle it makes with David's rope.
- *While sliding a couch across a floor, Andrea and Jennifer exert forces on the couch. Andrea’s force is due north with a magnitude of 130.0 N and Jennifer’s force is 32° east of north with a magnitude of 180.0 N.
(a) Find the magnitude and direction of the net force. - *A 30.0-kg girl in a swing is pushed to one side and held at rest by a horizontal force 𝐅⃗ so that the swing ropes are 30.0° with respect to the vertical.
(a) Calculate the tension in each of the two ropes supporting the swing under these conditions.
(b) Calculate the magnitude of 𝐅⃗ - *Two muscles in the back of the leg pull upward on the Achilles tendon, as shown below. (These muscles are called the medial and lateral heads of the gastrocnemius muscle.) Find the magnitude and direction of the total force on the Achilles tendon. What type of movement could be caused by this force?
- *After a mishap, a 76.0-kg circus performer clings to a trapeze, which is being pulled to the side by another circus artist, as shown here. Calculate the tension in the two ropes if the person is momentarily motionless. Include a free-body diagram in your solution.
- *Andrea, a 63.0-kg sprinter, starts a race with an acceleration of 4.200 m/s2. What is the net external force on her?
- *If the sprinter from the previous problem accelerates at that rate for 20.00 m and then maintains that velocity for the remainder of a 100.00-m dash, what will her time be for the race?
- *Astronauts in orbit are apparently weightless. This means that a clever method of measuring the mass of astronauts is needed to monitor their mass gains or losses, and adjust their diet. One way to do this is to exert a known force on an astronaut and measure the acceleration produced. Suppose a net external force of 50.0 N is exerted, and an astronaut’s acceleration is measured to be 0.893m/s2.
(a) Calculate her mass.
(b) By exerting a force on the astronaut, the vehicle in which she orbits experiences an equal and opposite force. Use this knowledge to find an equation for the acceleration of the system (astronaut and spaceship) that would be measured by a nearby observer.
(c) Discuss how this would affect the measurement of the astronaut’s acceleration. Propose a method by which recoil of the vehicle is avoided. - *Suppose two children push horizontally, but in exactly opposite directions, on a third child in a wagon. The first child exerts a force of 75.0 N, the second exerts a force of 90.0 N, friction is 12.0 N, and the mass of the third child plus wagon is 23.0 kg.
(a) What is the system of interest if the acceleration of the child in the wagon is to be calculated?
(b) Calculate the acceleration.
(c) What would the acceleration be if friction were 15.0 N?
- *A brave but inadequate rugby player is being pushed backward by an opposing player who is exerting a force of 800.0 N on him. The mass of the losing player plus equipment is 90.0 kg, and he is accelerating backward at 1.20m/s2.
(a) What is the force of friction between the losing player’s feet and the grass?(b) What force does the winning player exert on the ground to move forward if his mass plus equipment is 110.0 kg? - *When starting a foot race, a 70.0-kg sprinter exerts an average force of 650 N backward on the ground for 0.800 s.
(a) What is his final speed?
(b) How far does he travel? - *A basketball player jumps straight up for a ball. To do this, he lowers his body 0.300 m and then accelerates through this distance by forcefully straightening his legs. This player leaves the floor with a vertical velocity sufficient to carry him 0.900 m above the floor.
(a) Calculate his velocity when he leaves the floor.
(b) Calculate his acceleration while he is straightening his legs. He goes from zero to the velocity found in (a) in a distance of 0.300 m.
(c) Calculate the force he exerts on the floor to do this, given that his mass is 110.0 kg - &A soccer player starts from rest and accelerates forward, reaching a velocity of 8.00 m/s in 2.50 s. The player’s mass is 70.0 kg, and air resistance is negligible.
(a) What was his average acceleration?
(b) What average force did he exert backward on the ground to achieve this acceleration?
4.5 Problem-Solving Strategies
- A [latex]5\text{.}\text{00}×{\text{10}}^{5}\text{-kg}[/latex] rocket is accelerating straight up. Its engines produce [latex]1\text{.}\text{250}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex] of thrust, and air resistance is [latex]4\text{.}\text{50}×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex]. What is the rocket’s acceleration? Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
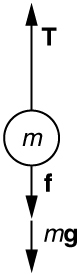
Solution: Using the free-body diagram:
[latex]{F}_{\text{net}}=T-f-mg=\text{ma}[/latex],
so that
[latex]a=\frac{T-f-\text{mg}}{m}=\frac{1\text{.}\text{250}×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{N}-4.50×{\text{10}}^{\text{6}}\phantom{\rule{0.25em}{0ex}}N-\left(5.00×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{kg}\right)\left(9.{\text{80 m/s}}^{2}\right)}{5.00×{\text{10}}^{5}\phantom{\rule{0.25em}{0ex}}\text{kg}}=\text{6.20}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}[/latex]. - Calculate the force a 70.0-kg high jumper must exert on the ground to produce an upward acceleration 4.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
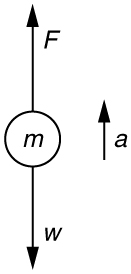
Solution: Use Newton’s laws of motion.
Given : [latex]a=4.00g=\left(4.00\right)\left(9.{\text{80 m/s}}^{2}\right)=\text{39.2}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}\text{;}\phantom{\rule{0.25em}{0ex}} m=\text{70}\text{.}\text{0 kg}[/latex],
Find: [latex]F[/latex].
[latex]\sum F\text{=+}F-w=\text{ma}\text{,}[latex] so that [latex] F=\text{ma}+w=\text{ma}+\text{mg}=m\left(a+g\right)[/latex].
[latex]F=\left(\text{70.0 kg}\right)\left[\left(\text{39}\text{.}{\text{2 m/s}}^{2}\right)+\left(9\text{.}{\text{80 m/s}}^{2}\right)\right]=3.\text{43}×{\text{10}}^{3}\text{N}[/latex]. The force exerted by the high-jumper is actually down on the ground, but [latex]F[/latex] is up from the ground and makes him jump.
This result is reasonable, since it is quite possible for a person to exert a force of the magnitude of [latex]{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{N}[/latex]. -
When landing after a spectacular somersault, a 40.0-kg gymnast decelerates by pushing straight down on the mat. Calculate the force she must exert if her deceleration is 7.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
- Two children pull a third child on a snow saucer sled exerting forces F1 and F2 as shown from below in the figure. Find the acceleration of the 49.00-kg sled and child system. Note that the direction of the frictional force is unspecified; it will be in the opposite direction of the sum of F1 and F2.
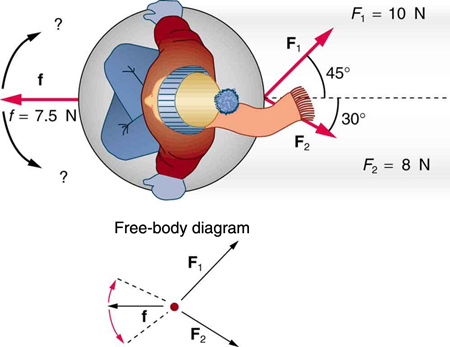
- The figure below shows Superhero and Trusty Sidekick hanging motionless from a rope. Superhero’s mass is 90.0 kg, while Trusty Sidekick’s is 55.0 kg, and the mass of the rope is negligible.
(a) Draw a free-body diagram of the situation showing all forces acting on Superhero, Trusty Sidekick, and the rope.
(b) Find the tension in the rope above Superhero.
(c) Find the tension in the rope between Superhero and Trusty Sidekick. Indicate on your free-body diagram the system of interest used to solve each part.
Superhero and Trusty Sidekick hang motionless on a rope as they try to figure out what to do next. Will the tension be the same everywhere in the rope?

- A nurse pushes a cart by exerting a force on the handle at a downward angle 35.0º below the horizontal. The loaded cart has a mass of 28.0 kg, and the force of friction is 60.0 N.
(a) Draw a free-body diagram for the system of interest.
(b) What force must the nurse exert to move at a constant velocity? - Construct Your Own Problem Consider the tension in an elevator cable during the time the elevator starts from rest and accelerates its load upward to some cruising velocity. Taking the elevator and its load to be the system of interest, draw a free-body diagram. Then calculate the tension in the cable. Among the things to consider are the mass of the elevator and its load, the final velocity, and the time taken to reach that velocity.
- Construct Your Own Problem Consider two people pushing a toboggan with four children on it up a snow-covered slope. Construct a problem in which you calculate the acceleration of the toboggan and its load. Include a free-body diagram of the appropriate system of interest as the basis for your analysis. Show vector forces and their components and explain the choice of coordinates. Among the things to be considered are the forces exerted by those pushing, the angle of the slope, and the masses of the toboggan and children?
- *The weight of an astronaut plus his space suit on the Moon is only 250 N.
(a) How much does the suited astronaut weigh on Earth?
(b) What is the mass on the Moon? On Earth? - *A body of mass 2.00 kg is pushed straight upward by a 25.0 N vertical force. What is its acceleration?
- *A fireman has mass m; he hears the fire alarm and slides down the pole with acceleration a (which is less than g in magnitude).
(a) Write an equation giving the vertical force he must apply to the pole.
(b) If his mass is 90.0 kg and he accelerates at 5.00m/s2, what is the magnitude of his applied force? - *A baseball catcher is performing a stunt for a television commercial. He will catch a baseball (mass 145 g) dropped from a height of 60.0 m above his glove. His glove stops the ball in 0.0100 s. What is the force exerted by his glove on the ball?
- *A leg is suspended in a traction system, as shown below.
(a) Which pulley in the figure is used to calculate the force exerted on the foot?
(b) What is the tension in the rope? Here 𝐓⃗ is the tension, 𝐰⃗ leg is the weight of the leg, and 𝐰⃗ is the weight of the load that provides the tension. - *Two teams of nine members each engage in a tug-of-war, pulling in opposite directions on a horizontal rope. Each of the first team’s members has an average mass of 68 kg and exerts an average force of 1350 N horizontally on the ground as they pull on the rope. Each of the second team’s members has an average mass of 73 kg and exerts an average force of 1365 N horizontally on the ground as they pull on the rope in the opposite direction.
(a) What is the magnitude of the acceleration of the two teams, and which team wins?(b) What is the tension in the section of rope between the teams? - *What force does a trampoline have to apply to Jennifer, a 45.0-kg gymnast, to accelerate her straight up at 7.50m/s2? The answer is independent of the velocity of the gymnast—she can be moving up or down or can be instantly stationary.
- *Suppose Kevin, a 60.0-kg gymnast, climbs a rope.
(a) What is the tension in the rope if he climbs at a constant speed?
(b) What is the tension in the rope if he accelerates upward at a rate of 1.50m/s2? - *A student’s backpack, full of textbooks, is hung from a spring scale attached to the ceiling of an elevator. When the elevator is accelerating downward at 3.8 m/s2, the scale reads 60 N.
(a) What is the mass of the backpack?
(b) What does the scale read if the elevator moves upward while speeding up at a rate3.8m/s2?
(c) What does the scale read if the elevator moves upward at constant velocity?
(d) If the elevator had no brakes and the cable supporting it were to break loose so that the elevator could fall freely, what would the spring scale read? - A ball of mass m hangs at rest, suspended by a string.
(a) Sketch all forces.
(b) Draw the free-body diagram for the ball. - *A runner pushes against the track, as shown.
(a) Provide a free-body diagram showing all the forces on the runner. (Hint: Place all forces at the center of his body, and include his weight.)
(b) Give a revised diagram showing the xy-component form. - *Draw a free-body diagram of a diver who has entered the water, moved downward, and is acted on by an upward force due to the water which balances the weight (that is, the diver is suspended).
- (a) What is the maximum frictional force in the knee joint of a person who supports 66.0 kg of her mass on that knee?
(b) During strenuous exercise, it is possible to exert forces to the joints that are easily 10 times greater than the weight being supported. What is the maximum force of friction under such conditions? The frictional forces in joints are relatively small in all circumstances except when the joints deteriorate, such as from injury or arthritis. Increased frictional forces can cause further damage and pain.
Solution: a. 10.0 N; b. 97.0 N - Suppose you have a 120-kg wooden crate resting on a wood floor, with coefficient of static friction 0.500 between these wood surfaces.
(a) What maximum force can you exert horizontally on the crate without moving it?
(b) If you continue to exert this force once the crate starts to slip, what will its acceleration then be? The coefficient of sliding friction is known to be 0.300 for this situation. - A team of eight dogs pulls a sled with waxed wood runners on wet snow (mush!). The dogs have average masses of 19.0 kg, and the loaded sled with its rider has a mass of 210 kg.
(a) Calculate the acceleration of the dogs starting from rest if each dog exerts an average force of 185 N backward on the snow.
(b) Calculate the force in the coupling between the dogs and the sled. - Consider the 65.0-kg ice skater being pushed by two others shown below.
(a) Find the direction and magnitude of [latex]{F}_{\text{tot}}[/latex] the total force exerted on her by the others, given that the magnitudes [latex]{F}_{1}[/latex] and [latex]{F}_{2}[/latex] are 26.4 N and 18.6 N, respectively.
(b) What is her initial acceleration if she is initially stationary and wearing steel-bladed skates that point in the direction of [latex]{F}_{\text{tot}}[/latex]
(c) What is her acceleration assuming she is already moving in the direction of [latex]{F}_{\text{tot}}[/latex]? (Remember that friction always acts in the direction opposite that of motion or attempted motion between surfaces in contact.) Solution: a. 32.3 N, 35.2°; b. 0; c. [latex]0.301\,{\text{m/s}}^{2}[/latex] in the direction of [latex]{\overset{\to }{F}}_{\text{tot}}[/latex]
Solution: a. 32.3 N, 35.2°; b. 0; c. [latex]0.301\,{\text{m/s}}^{2}[/latex] in the direction of [latex]{\overset{\to }{F}}_{\text{tot}}[/latex] - Show that the acceleration of any object down a frictionless incline that makes an angle [latex]\theta[/latex] with the horizontal is [latex]a=g\,\text{sin}\,\theta[/latex]. (Note that this acceleration is independent of mass.)

- Calculate the deceleration of a snow boarder going up a 5.00° slope, assuming the coefficient of friction for waxed wood on wet snow. The result of the preceding problem may be useful, but be careful to consider the fact that the snow boarder is going uphill.
- If an object is to rest on an incline without slipping, then friction must equal the component of the weight of the object parallel to the incline. This requires greater and greater friction for steeper slopes. Show that the maximum angle of an incline above the horizontal for which an object will not slide down is [latex]\theta ={\text{tan}}^{-1}\,{\mu }_{\text{s}}.[/latex] You may use the result of the previous problem. Assume that [latex]a=0[/latex] and that static friction has reached its maximum value.

- Consider the 52.0-kg mountain climber shown below.
(a) Find the tension in the rope and the force that the mountain climber must exert with her feet on the vertical rock face to remain stationary. Assume that the force is exerted parallel to her legs. Also, assume negligible force exerted by her arms.
(b) What is the minimum coefficient of friction between her shoes and the cliff? Solution: a. 272 N, 512 N; b. 0.268
Solution: a. 272 N, 512 N; b. 0.268 - A contestant in a winter sporting event pushes a 45.0-kg block of ice across a frozen lake as shown below.
(a) Calculate the minimum force F he must exert to get the block moving.
(b) What is its acceleration once it starts to move, if that force is maintained?
- The contestant now pulls the block of ice with a rope over his shoulder at the same angle above the horizontal as shown below. Calculate the minimum force F he must exert to get the block moving. (b) What is its acceleration once it starts to move, if that force is maintained?
 Solution: a. 46.5 N; b. [latex]0.629\,{\text{m/s}}^{2}[/latex]
Solution: a. 46.5 N; b. [latex]0.629\,{\text{m/s}}^{2}[/latex] - *(a) What is the maximum frictional force in the knee joint of a person who supports 66.0 kg of her mass on that knee?
(b) During strenuous exercise, it is possible to exert forces to the joints that are easily 10 times greater than the weight being supported. What is the maximum force of friction under such conditions?
The frictional forces in joints are relatively small in all circumstances except when the joints deteriorate, such as from injury or arthritis. Increased frictional forces can cause further damage and pain. - At a post office, a parcel that is a 20.0-kg box slides down a ramp inclined at 30.0° with the horizontal. The coefficient of kinetic friction between the box and plane is 0.0300.
(a) Find the acceleration of the box.
(b) Find the velocity of the box as it reaches the end of the plane, if the length of the plane is 2 m and the box starts at rest.
- The terminal velocity of a person falling in air depends upon the weight and the area of the person facing the fluid. Find the terminal velocity (in meters per second and kilometers per hour) of an 80.0-kg skydiver falling in a headfirst position with a surface area of [latex]0\text{.}\text{140}\phantom{\rule{0.25em}{0ex}}{\text{m}}^{2}[/latex].
Solution: [latex]\text{115}\phantom{\rule{0.25em}{0ex}}\text{m/s;}\phantom{\rule{0.25em}{0ex}}\text{414}\phantom{\rule{0.25em}{0ex}}\text{km/hr}[/latex] - A 60-kg and a 90-kg skydiver jump from an airplane at an altitude of 6000 m, both falling in a headfirst position. Make some assumption on their frontal areas and calculate their terminal velocities. How long will it take for each skydiver to reach the ground (assuming the time to reach terminal velocity is small)? Assume all values are accurate to three significant digits.
- A 560-g squirrel with a surface area of [latex]\text{930}\phantom{\rule{0.25em}{0ex}}{\text{cm}}^{2}[/latex] falls from a 5.0-m tree to the ground. Estimate its terminal velocity. (Use a drag coefficient for a horizontal skydiver.) What will be the velocity of a 56-kg person hitting the ground, assuming no drag contribution in such a short distance?
Solution: [latex]\text{25 m/s; 9.9 m/s}[/latex] - Suppose that the resistive force of the air on a skydiver can be approximated by 𝑓=−𝑏𝑣2. If the terminal velocity of a 50.0-kg skydiver is 60.0 m/s, what is the value of b?
- During a circus act, one performer swings upside down hanging from a trapeze holding another, also upside-down, performer by the legs. If the upward force on the lower performer is three times her weight, how much do the bones (the femurs) in her upper legs stretch? You may assume each is equivalent to a uniform rod 35.0 cm long and 1.80 cm in radius. Her mass is 60.0 kg.
Solution: [latex]1\text{.}\text{90}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{cm}[/latex] - During a wrestling match, a 150 kg wrestler briefly stands on one hand during a maneuver designed to perplex his already moribund adversary. By how much does the upper arm bone shorten in length? The bone can be represented by a uniform rod 38.0 cm in length and 2.10 cm in radius.
- TV broadcast antennas are the tallest artificial structures on Earth. In 1987, a 72.0-kg physicist placed himself and 400 kg of equipment at the top of one 610-m high antenna to perform gravity experiments. By how much was the antenna compressed, if we consider it to be equivalent to a steel cylinder 0.150 m in radius?
- (a) By how much does a 65.0-kg mountain climber stretch her 0.800-cm diameter nylon rope when she hangs 35.0 m below a rock outcropping?
(b) Does the answer seem to be consistent with what you have observed for nylon ropes? Would it make sense if the rope were actually a bungee cord?
Solution: (a)9 cm; (b)This seems reasonable for nylon climbing rope, since it is not supposed to stretch that much. - Calculate the force a piano tuner applies to stretch a steel piano wire 8.00 mm, if the wire is originally 0.850 mm in diameter and 1.35 m long.
- A vertebra is subjected to a shearing force of 500 N. Find the shear deformation, taking the vertebra to be a cylinder 3.00 cm high and 4.00 cm in diameter.
Solution: [latex]1\text{.}\text{49}×{\text{10}}^{-7}\phantom{\rule{0.25em}{0ex}}\text{m}[/latex] - A disk between vertebrae in the spine is subjected to a shearing force of 600 N. Find its shear deformation, taking it to have the shear modulus of [latex]1×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}\text{N}/{\text{m}}^{2}[/latex] . The disk is equivalent to a solid cylinder 0.700 cm high and 4.00 cm in diameter.
- A farmer making grape juice fills a glass bottle to the brim and caps it tightly. The juice expands more than the glass when it warms up, in such a way that the volume increases by 0.2% (that is, [latex]\Delta V/{V}_{0}=2×{\text{10}}^{-3}[/latex]) relative to the space available. Calculate the magnitude of the normal force exerted by the juice per square centimeter if its bulk modulus is [latex]1\text{.}8×{\text{10}}^{9}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex], assuming the bottle does not break. In view of your answer, do you think the bottle will survive?
Solution: [latex]4×{\text{10}}^{6}\phantom{\rule{0.25em}{0ex}}{\text{N/m}}^{2}[/latex]. This is about 36 atm, greater than a typical jar can withstand. - This problem returns to the tightrope walker studied in (Figure), who created a tension of [latex]3\text{.}\text{94}×{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}N\[/latex] in a wire making an angle 5.0º below the horizontal with each supporting pole. Calculate how much this tension stretches the steel wire if it was originally 15 m long and 0.50 cm in diameter.
Solution: 1.4 cm
4.11 Further Applications of Newton's Laws of Motion
- *A 75.0-kg woman stands on a bathroom scale in an elevator that accelerates from rest to 30.0 m/s in 2.00 s.
(a) Calculate the scale reading in newtons and compare it with her weight. (The scale exerts an upward force on her equal to its reading.)
(b) What is unreasonable about the result?
(c) Which premise is unreasonable, or which premises are inconsistent? - &Calculate the force a 70.0-kg high jumper must exert on the ground to produce an upward acceleration 4.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
- &When landing after a spectacular somersault, a 40.0-kg gymnast decelerates by pushing straight down on the mat. Calculate the force she must exert if her deceleration is 7.00 times the acceleration due to gravity. Explicitly show how you follow the steps in the Problem-Solving Strategy for Newton’s laws of motion.
- *For a swimmer who has just jumped off a diving board, assume air resistance is negligible. The swimmer has a mass of 80.0 kg and jumps off a board 10.0 m above the water. Three seconds after entering the water, her downward motion is stopped. What average upward force did the water exert on her?
- *A child has mass 6.0 kg and slides down a 35° incline with constant speed under the action of a 34-N force acting up and parallel to the incline. What is the coefficient of kinetic friction between the child and the surface of the incline?
- *Two forces of 25 and 45 N act on an object. Their directions differ by 70°. The resulting acceleration has magnitude of [latex]10.0\,{\text{m/s}}^{2}[/latex] What is the mass of the body?
Solution: 5.90 kg - *A force of 1600 N acts parallel to a ramp to push a 300-kg piano into a moving van. The ramp is inclined at 20°.
(a) What is the acceleration of the piano up the ramp?
(b) What is the velocity of the piano when it reaches the top if the ramp is 4.0 m long and the piano starts from rest? -
*Draw a free-body diagram of a diver who has entered the water, moved downward, and is acted on by an upward force due to the water which balances the weight (that is, the diver is suspended).
- *For a swimmer who has just jumped off a diving board, assume air resistance is negligible. The swimmer has a mass of 80.0 kg and jumps off a board 10.0 m above the water. Three seconds after entering the water, her downward motion is stopped. What average upward force did the water exert on her?
- *A body of mass 2.0 kg is moving along the x-axis with a speed of 3.0 m/s at the instant represented below.
(a) What is the acceleration of the body?
(b) What is the body’s velocity 10.0 s later?
(c) What is its displacement after 10.0 s

- *Two boxes, A and B, are at rest. Box A is on level ground, while box B rests on an inclined plane tilted at angle [latex]\theta[/latex] with the horizontal.
(a) Write expressions for the normal force acting on each block.
(b) Compare the two forces; that is, tell which one is larger or whether they are equal in magnitude.
(c) If the angle of incline is 10°, which force is greater?
Solution: a. For box A, [latex]{N}_{\text{A}}=mg[/latex] and [latex]{N}_{\text{B}}=mg\,\text{cos}\,\theta[/latex]; b. [latex]{N}_{\text{A}}>{N}_{\text{B}}[/latex] because for [latex]\theta <90\text{°}[/latex], [latex]\text{cos}\,\theta <1[/latex]; c. [latex]{N}_{\text{A}}>{N}_{\text{B}}[/latex] when [latex]\theta =10\text{°}[/latex] - *(a) What is the final velocity of a car originally traveling at 50.0 km/h that accelerates opposite to the motion at a rate of 0.400m/s2
for 50.0 s? Assume a coefficient of friction of 1.0.
(b) What is unreasonable about the result?
(c) Which premise is unreasonable, or which premises are inconsistent? - *A 75.0-kg woman stands on a bathroom scale in an elevator that accelerates from rest to 30.0 m/s in 2.00 s.
(a) Calculate the scale reading in newtons and compare it with her weight. (The scale exerts an upward force on her equal to its reading.)
(b) What is unreasonable about the result?
(c) Which premise is unreasonable, or which premises are inconsistent?
Solution: (a) 1860 N, 2.53; (b) The value (1860 N) is more force than you expect to experience on an elevator. The force of 1860 N is 418 pounds, compared to the force on a typical elevator of 904 N (which is about 203 pounds); this is calculated for a speed from 0 to 10 miles per hour, which is about 4.5 m/s, in 2.00 s). (c) The acceleration a=1.53×g is much higher than any standard elevator. The final speed is too large (30.0 m/s is VERY fast)! The time of 2.00 s is not unreasonable for an elevator. - *(a) Calculate the minimum coefficient of friction needed for a car to negotiate an unbanked 50.0 m radius curve at 30.0 m/s.
(b) What is unreasonable about the result?
(c) Which premises are unreasonable or inconsistent? - *A child has mass 6.0 kg and slides down a 35° incline with constant speed under the action of a 34-N force acting up and parallel to the incline. What is the coefficient of kinetic friction between the child and the surface of the incline?
- *A box is dropped onto a conveyor belt moving at 3.4 m/s. If the coefficient of friction between the box and the belt is 0.27, how long will it take before the box moves without slipping?
Solution: 1.3 s
- *On June 25, 1983, shot-putter Udo Beyer of East Germany threw the 7.26-kg shot 22.22 m, which at that time was a world record.
(a) If the shot was released at a height of 2.20 m with a projection angle of 45.0°, what was its initial velocity?
(b) If while in Beyer’s hand the shot was accelerated uniformly over a distance of 1.20 m, what was the net force on it? - *A 120-kg astronaut is riding in a rocket sled that is sliding along an inclined plane. The sled has a horizontal component of acceleration of 5.0m/s2 and a downward component of 3.8m/s2. Calculate the magnitude of the force on the rider by the sled. (Hint: Remember that gravitational acceleration must be considered.)
- *Suppose that you are viewing a soccer game from a helicopter above the playing field. Two soccer players simultaneously kick a stationary soccer ball on the flat field; the soccer ball has mass 0.420 kg. The first player kicks with force 162 N at 9.0° north of west. At the same instant, the second player kicks with force 215 N at 15° east of south. Find the acceleration of the ball in the x (East/West) and y (North/South) directions.
- *A skydiver is at an altitude of 1520 m. After 10.0 seconds of free fall, he opens his parachute and finds that the air resistance, 𝐹D, is given by the formula 𝐹D=−𝑏𝑣, where b is a constant and v is the velocity. If 𝑏=0.750, and the mass of the skydiver is 82.0 kg, first set up differential equations for the velocity and the position, and then find:
(a) the speed of the skydiver when the parachute opens,
(b) the distance fallen before the parachute opens,
(c) the terminal velocity after the parachute opens (find the limiting velocity), and
(d) the time the skydiver is in the air after the parachute opens. - *If two tugboats pull on a disabled vessel, as shown here in an overhead view, the disabled vessel will be pulled along the direction indicated by the result of the exerted forces.
(a) Draw a free-body diagram for the vessel. Assume no friction or drag forces affect the vessel.
(b) Did you include all forces in the overhead view in your free-body diagram? Why or why not?

- *A 10.0-kg object is initially moving east at 15.0 m/s. Then a force acts on it for 2.00 s, after which it moves northwest, also at 15.0 m/s. What are the magnitude and direction of the average force that acted on the object over the 2.00-s interval?

