4.6 Mass and Weight

Weight and Gravitational Force

When an object is dropped, it accelerates toward the center of Earth. Newton’s second law says that a net force on an object is responsible for its acceleration. If air resistance is negligible, the net force on a falling object is the gravitational force, commonly called its weight [latex]\overset{\to }{w}[/latex], or the force due to gravity (acting on the mass of the object). Therefore, weight is a vector because it has a direction; down is, by definition, the direction of gravity, and hence, weight is a downward force. Galileo was instrumental in showing that, in the absence of air resistance, all objects fall with the same acceleration g. Using Galileo’s result and Newton’s second law, we can derive an equation for weight.

Consider an object with mass m falling toward Earth. It experiences only the downward force of gravity, which is the weight [latex]\overset{\to }{w}[/latex]. Newton’s second law says that the magnitude of the net external force on an object is [latex]{\overset{\to }{F}}_{\text{net}}=m\overset{\to }{a}.[/latex] We know that the acceleration of an object due to gravity is [latex]\overset{\to }{g},[/latex] or [latex]\overset{\to }{a}=\overset{\to }{g}[/latex]. Substituting these into Newton’s second law gives us the following:

Since [latex]g=9.80\,{\text{m/s}}^{2}[/latex] on Earth, the weight of a 1.00-kg object on Earth is 9.80 N:

[latex]w=mg=(1.00\,\text{kg})({9.80\,\text{m/s}}^{2})=9.80\,\text{N}.[/latex]

When the net external force on an object is its weight, we say that it is in free fall, that is, the only force acting on the object is gravity. However, when objects on Earth fall downward, they are never truly in free fall because there is always some upward resistance force from the air acting on the object.

Acceleration due to gravity g varies slightly over the surface of Earth, so the weight of an object depends on its location and is not an intrinsic property of the object. Weight varies dramatically if we leave Earth’s surface. On the Moon, for example, acceleration due to gravity is only [latex]{1.67\,\text{m/s}}^{2}[/latex]. A 1.0-kg mass thus has a weight of 9.8 N on Earth and only about 1.7 N on the Moon.

The broadest definition of weight in this sense is that the weight of an object is the gravitational force on it from the nearest large body, such as Earth, the Moon, or the Sun. This is the most common and useful definition of weight in biomechanics. It differs dramatically, however, from the definition of weight used by the lay public in relation to space travel and exploration. When they speak of “weightlessness” and “microgravity,” they are referring to the phenomenon we call “free fall” in physics.

Be aware that weight and mass are different physical quantities, although they are closely related. Mass is an intrinsic property of an object: It is a quantity of matter. The quantity or amount of matter of an object is determined by the numbers of atoms and molecules of various types it contains. Because these numbers do not vary, in Newtonian mechanics, mass does not vary; therefore, its response to an applied force does not vary. In contrast, weight is the gravitational force acting on an object, so it does vary depending on gravity. For example, a person closer to the center of Earth, at a low elevation such as New Orleans, weighs slightly more than a person who is located in the higher elevation of Denver, even though they may have the same mass.

It is tempting to equate mass to weight, because most of our examples take place on Earth, where the weight of an object varies only a little with the location of the object. In addition, it is difficult to count and identify all of the atoms and molecules in an object, so mass is rarely determined in this manner. If we consider situations in which [latex]\overset{\to }{g}[/latex] is a constant on Earth, we see that weight [latex]\overset{\to }{w}[/latex] is directly proportional to mass m, since [latex]\overset{\to }{w}=m\overset{\to }{g},[/latex] that is, the more massive an object is, the more it weighs. Operationally, the masses of objects are determined by comparison with the standard kilogram, as we discussed in Units and Measurement. But by comparing an object on Earth with one on the Moon, we can easily see a variation in weight but not in mass. For instance, on Earth, a 5.0-kg object weighs 49 N; on the Moon, where g is [latex]{1.67\,\text{m/s}}^{2}[/latex], the object weighs 8.4 N. However, the mass of the object is still 5.0 kg on the Moon.

Example: Bicep curl exercise – mass, weight and acceleration

Suppose you are in the gym doing bicep curl exercises with a 40 lb dumbbell.

a) What is the mass and weight of the dumbbell?

b) How much force do you need to exert on the dumbbell in order to hold stationary?

c) How much force do you need to exert on the dumbbell in order to accelerate it upwards at 1.5 m/s²?

Strategy

First we must convert the ‘weight’ of the dumbbell in pounds into the correct units of mass (kg). Then for b) and c) we can consider whether the dumbbell is in equilibrium and using a free-body diagram, solve for force our hand must exert on the dumbbell.

Solution

a) 1 kg = 2.21 lbs, so using our principles of conversion:

[latex]40 \text{lb} * \frac{1 \text{kg}}{2.21 \text{lbs}} = 18.1 \text {kg}[/latex]

and now we can covert to weight (in Newtons), using w = mg:

[latex]w = \text{mg} = 18.1 \text{kg} * 9.81\,{\text{m/s}}^{2} = 177.6 N[/latex]

note: by definition weight is a vector and so since both the gravitational acceleration and weight are positive in the above calculation, we are essentially saying that weight is acting in the same direction as gravity. We have defined gravity as positive for convenience. This is ok for isolated calculations of weight, however when doing this in the context of a free body diagram or other forces we must be careful. See b) below.

b) First, let’s draw a free body diagram. This will help us think about the forces acting on the dumbbell. Since no forces act in the horizontal direction we can concentrate on the vertical forces. We can also label the acceleration to the side; technically, it is not part of the free-body diagram, but it helps to remind us that the object accelerates upward in part c (so the net force must be is upward).

Now, continuing with part b): if the object is stationary then it is equilibrium and we can apply Newton’s First Law. That is:

[latex]\sum F = 0[/latex]

Since we two forces, weight and the force of our hand:

[latex]\sum F = w + F_{hand} = 0[/latex]

and so,

[latex]F_{hand} = -w = - \left(-177.6 N\right)[/latex]

note: we must remember that weight is acting downwards and so as a vector it is -177.6 N. Alternatively, we could include the direction of the gravitational acceleration in a) above to yield -177.6 N for weight.

 

c) Now the dumbbell is accelerating upwards at 1.5 m/s². This means the object is no longer in equilibrium and we must use Newton’s Second Law:

[latex]\sum F = \text{ma}[/latex]

Incorporating the two forces, we get:

[latex]w + F_{hand} = ma[/latex]

And solving for F_hand:

[latex]F_{hand} = ma - w = 18.1 \text{kg}*1.5\,{\text{m/s}}^{2} - \left(-177.6 N\right) = 27.2 N + 177.6 N = 204.8N[/latex]

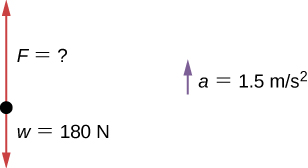
Discussion

We must be careful in distinguishing mass and weight. Free body diagrams can help us carefully think about the forces acting on an object and which equation or Newton’s Law to use.

In the case of lifting a dumbbell upwards, an acceleration must be applied in order to change it’s velocity from zero (when it’s stationary). For the initial upwards acceleration this means a force greater than just the weight of the object must be applied. In this case, it was an addition 27.2N beyond the weight of the object.