Chapter 3 Describing Movement in Two Dimensions, 2-D Linear Kinematics
Problems & Exercises
3.2 Adding and Subtracting Vectors: Graphical
Use graphical methods to solve these problems. You may assume data taken from graphs is accurate to three digits.
- Find the following for path A in the figure:
(a) the total distance traveled, and
(b) the magnitude and direction of the displacement from start to finish.
The various lines represent paths taken by different people walking in a city. All blocks are 120 m on a side.
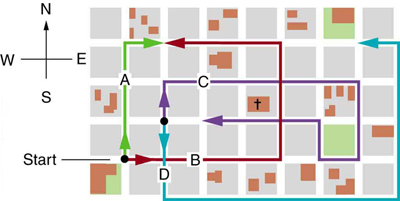Solution: (a) 480 m; (b) 379 m, 18.4º east of north - Find the following for path B in thee figure above:
(a) the total distance traveled, and
(b) the magnitude and direction of the displacement from start to finish.
Solution: (a) 1200m; b) 379m, 18.4º east of north (or 71.6º north of east) - Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements [latex]\mathbf{A}[/latex] and [latex]\mathbf{B}[/latex], then this problem asks you to find their sum [latex]\mathbf{R}=\mathbf{A}+\mathbf{B}[/latex].)
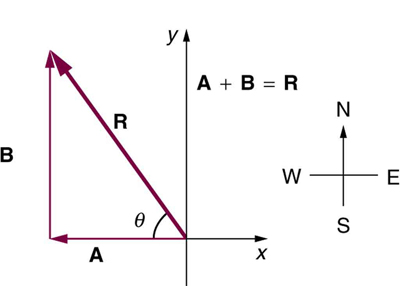Solution: 30.8m away from the starting point at a direction of 54.3º north of west - Suppose you first walk 12.0 m in a direction 20º west of north and then 20.0 m in a direction 40.0º south of west. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements [latex]\mathbf{A}[/latex] and [latex]\mathbf{B}[/latex], then this problem asks you to find their sum [latex]\mathbf{R}=\mathbf{A}+\mathbf{B}[/latex].)
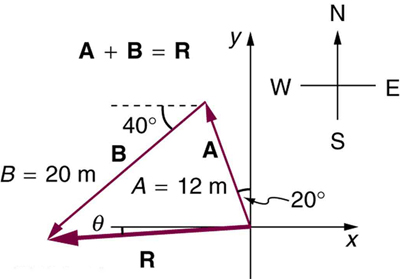
Solution: 19.5 m, 4.65º south of west - Repeat the problem above, but reverse the order of the two legs of the walk; show that you get the same final result. That is, you first walk leg [latex]\mathbf{B}[/latex], which is 20.0 m in a direction exactly 40º south of west, and then leg [latex]\mathbf{A}[/latex], which is 12.0 m in a direction exactly 20º west of north. (This problem shows that [latex]\mathbf{A}+\mathbf{B}=\mathbf{B}+\mathbf{A}[/latex].)
(a) Repeat the problem two problems prior, but for the second leg you walk 20.0 m in a direction 40.0º north of east (which is equivalent to subtracting [latex]\mathbf{\text{B}}[/latex] from [latex]\mathbf{A}[/latex] —that is, to finding [latex]\mathbf{\text{R}}\prime =\mathbf{\text{A}}-\mathbf{\text{B}}[/latex]).
(b) Repeat the problem two problems prior, but now you first walk 20.0 m in a direction 40.0º south of west and then 12.0 m in a direction 20.0º east of south (which is equivalent to subtracting [latex]\mathbf{\text{A}}[/latex] from [latex]\mathbf{\text{B}}[/latex] —that is, to finding [latex]). Show that this is the case. Solution: (a) 26.6 m, 65.1º north of east; (b) 26.6 m, 65.1º south of west - Show that the order of addition of three vectors does not affect their sum. Show this property by choosing any three vectors [latex]\mathbf{A}[/latex], [latex]\mathbf{B}[/latex], and [latex]\mathbf{C}[/latex], all having different lengths and directions. Find the sum [latex]\text{A + B + C}[/latex] then find their sum when added in a different order and show the result is the same. (There are five other orders in which [latex]\mathbf{A}[/latex], [latex]\mathbf{B}[/latex], and [latex]\mathbf{C}[/latex] can be added; choose only one.)
3.3 Adding and Subtracting Vectors: Algebra
- Find the following for path C in the figure:
(a) the total distance traveled and
(b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.
The various lines represent paths taken by different people walking in a city. All blocks are 120 m on a side.
Solution: (a) 1.56 km; (b) 120 m east - Find the following for path D in thee figure above:
(a) the total distance traveled and
(b) the magnitude and direction of the displacement from start to finish. In this part of the problem, explicitly show how you follow the steps of the analytical method of vector addition.
Solution: (a) 1.56 km; (b) 646 m at a direction of 21 degrees north of east - Find the north and east components of the displacement from San Francisco to Sacramento shown in thee figure.
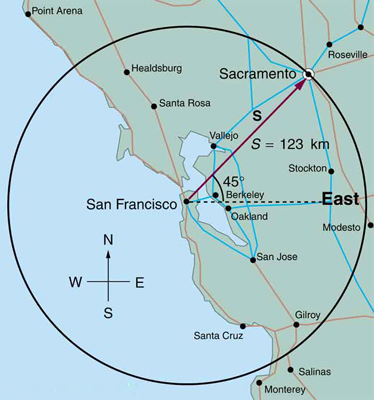Solution: North-component 87.0 km, east-component 87.0 km - Solve the following problem using analytical techniques: Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point, and what is the compass direction of a line connecting your starting point to your final position? (If you represent the two legs of the walk as vector displacements [latex]\mathbf{A}[/latex] and [latex]\mathbf{B}[/latex], then this problem asks you to find their sum [latex]\mathbf{R}=\mathbf{A}+\mathbf{B}[/latex].)Note that you can also solve the question above graphically. Discuss why the analytical technique for solving this problem is potentially more accurate than the graphical technique.
Solution: see 3.3 #3 above; analytical (trigonometric) techniques are more accurate because any error in the accuracy of the drawing and measuring during the graphical approach is eliminated.
- You drive 7.50 km in a straight line in a direction 15º east of north.
(a) Find the distances you would have to drive straight east and then straight north to arrive at the same point. (This determination is equivalent to find the components of the displacement along the east and north directions.)
(b) Show that you still arrive at the same point if the east and north legs are reversed in order.
Solution: (a) east: 1.9km; north: 7.3 km; (b) this could either be shown graphically by drawing the components of the vectors in the opposite order, or analytically as the order of components is irrelevant in the various formulas
- You fly 32.0 km in a straight line in still air in the direction 35.0º south of west.
(a) Find the distances you would have to fly straight south and then straight west to arrive at the same point. (This determination is equivalent to finding the components of the displacement along the south and west directions.)
(b) Find the distances you would have to fly first in a direction 45.0º south of west and then in a direction 45.0º west of north. These are the components of the displacement along a different set of axes—one rotated 45º.
Solution: (a) 18.4 km south, then 26.2 km west; (b) 31.5 km at 45.0º south of west, then 5.56 km at 45.0º west of north - In an attempt to escape his island, Gilligan builds a raft and sets to sea. The wind shifts a great deal during the day, and he is blown along the following straight lines: 2.50 km 45.0º north of west; then 4.70 km 60.0º south of east; then 1.30 km 25.0º south of west; then 5.10 km straight east; then 1.70 km 5.00º east of north; then 7.20 km 55.0º south of west; and finally 2.80 km 10.0º north of east. What is his final position relative to the island?
Solution: 7.34 km, 63.5º south of east
3.4 Projectile Motion
- A soccer ball is kicked at ground level with an initial speed of 15 m/s at an angle of 30.0º above the horizontal. How far and how high did the ball go before it hit the ground?
Solution: It reached a height of 2.9m and travelled a distance of 19.9m before hitting the ground. - A ball is kicked with an initial velocity of 16 m/s in the horizontal direction and 12 m/s in the vertical direction.
(a) At what speed does the ball hit the ground?
(b) For how long does the ball remain in the air?
(c)What maximum height is attained by the ball?
Solution: (a) 12 m/s; (b) 3.3 seconds; (c); 13 m - A ball is thrown horizontally from the top of a 60.0-m building and lands 100.0 m from the base of the building. Ignore air resistance.
(a) How long is the ball in the air?
(b) What must have been the initial horizontal component of the velocity?
(c) What is the vertical component of the velocity just before the ball hits the ground?
(d) What is the velocity (including both the horizontal and vertical components) of the ball just before it hits the ground?
Solution: (a) 3.50 s; (b) 28.6 m/s; (c) 34.3 m/s; (d) 44.7 m/s, 50.2º below horizontal - (a) A daredevil is attempting to jump his motorcycle over a line of buses parked end to end by driving up a 32º ramp at a speed of 40.0 m/s (144 km/h). How many buses can he clear if the top of the takeoff ramp is at the same height as the bus tops and the buses are 20.0 m long?
(b) Discuss what your answer implies about the margin of error in this act—that is, consider how much greater the range is than the horizontal distance he must travel to miss the end of the last bus. (Neglect air resistance.) - An archer shoots an arrow at a 75.0 m distant target; the bull’s-eye of the target is at same height as the release height of the arrow.
(a) At what angle must the arrow be released to hit the bull’s-eye if its initial speed is 35.0 m/s? In this part of the problem, explicitly show how you follow the steps involved in solving projectile motion problems.
(b) There is a large tree halfway between the archer and the target with an overhanging horizontal branch 3.50 m above the release height of the arrow. Will the arrow go over or under the branch?
Solution: (a) 18.4º; (b) The arrow will go over the branch. - A rugby player passes the ball 7.00 m across the field, where it is caught at the same height as it left his hand.
(a) At what angle was the ball thrown if its initial speed was 12.0 m/s, assuming that the smaller of the two possible angles was used?
(b) What other angle gives the same range, and why would it not be used?
(c) How long did this pass take? - An arrow is shot from a height of 1.5 m toward a cliff of height [latex]H[/latex]. It is shot with a velocity of 30 m/s at an angle of 60º above the horizontal. It lands on the top edge of the cliff 4.0 s later.
(a) What is the height of the cliff?
(b) What is the maximum height reached by the arrow along its trajectory?
(c) What is the arrow’s impact speed just before hitting the cliff? - In the standing broad jump, one squats and then pushes off with the legs to see how far one can jump. Suppose the extension of the legs from the crouch position is 0.600 m and the acceleration achieved from this position is 1.25 times the acceleration due to gravity, [latex]g[/latex]. How far can they jump? State your assumptions. (Increased range can be achieved by swinging the arms in the direction of the jump.)
Solution: 1.50 m, assuming launch angle of 45º - The world long jump record is 8.95 m (Mike Powell, USA, 1991). Treated as a projectile, what is the maximum range obtainable by a person if he has a take-off speed of 9.5 m/s? State your assumptions.
- Serving at a speed of 170 km/h, a tennis player hits the ball at a height of 2.5 m and an angle [latex]\theta[/latex] below the horizontal. The base line is 11.9 m from the net, which is 0.91 m high.
(a) What is the angle [latex]\theta[/latex] such that the ball just crosses the net?
(b)Will the ball land in the service box, whose service line is 6.40 m from the net?
Solution: (a) [latex]\theta =6.1º[/latex]; (b) yes, the ball lands at 5.3 m from the net - A football quarterback is moving straight backward at a speed of 2.00 m/s when he throws a pass to a player 18.0 m straight downfield.
(a) If the ball is thrown at an angle of 25º relative to the ground and is caught at the same height as it is released, what is its initial speed relative to the ground?
(b) How long does it take to get to the receiver?
(c) What is its maximum height above its point of release? - Gun sights are adjusted to aim high to compensate for the effect of gravity, effectively making the gun accurate only for a specific range.
(a) If a gun is sighted to hit targets that are at the same height as the gun and 100.0 m away, how low will the bullet hit if aimed directly at a target 150.0 m away? The muzzle velocity of the bullet is 275 m/s.
(b) Discuss qualitatively how a larger muzzle velocity would affect this problem and what would be the effect of air resistance.
Solution: (a) −0.486 m; (b) The larger the muzzle velocity, the smaller the deviation in the vertical direction, because the time of flight would be smaller. Air resistance would have the effect of decreasing the time of flight, therefore increasing the vertical deviation. - Suppose a soccer player kicks the ball from a distance 30 m toward the goal. Find the initial speed of the ball if it just passes over the goal, 2.4 m above the ground, given the initial direction to be 40º above the horizontal.
Solution: 10.7 m/s - Can a goalkeeper at her/ his goal kick a soccer ball into the opponent’s goal without the ball touching the ground? The distance will be about 95 m. A goalkeeper can give the ball a speed of 30 m/s.
Solution: No, the maximum range (neglecting air resistance) is about 92 m. - The free throw line in basketball is 4.57 m (15 ft) from the basket, which is 3.05 m (10 ft) above the floor. A player standing on the free throw line throws the ball with an initial speed of 8.15 m/s, releasing it at a height of 2.44 m (8 ft) above the floor. At what angle above the horizontal must the ball be thrown to exactly hit the basket? Note that most players will use a large initial angle rather than a flat shot because it allows for a larger margin of error. Explicitly show how you follow the steps involved in solving projectile motion problems.
- In 2007, Michael Carter (U.S.) set a world record in the shot put with a throw of 24.77 m. What was the initial speed of the shot if he released it at a height of 2.10 m and threw it at an angle of 38.0º above the horizontal? (Although the maximum distance for a projectile on level ground is achieved at 45º when air resistance is neglected, the actual angle to achieve maximum range is smaller; thus, 38º will give a longer range than 45º in the shot put.)
Solution: 15.0 m/s - A basketball player is running at 5.00 m/s directly toward the basket when he jumps into the air to dunk the ball. He maintains his horizontal velocity.
(a) What vertical velocity does he need to rise 0.750 m above the floor?
(b) How far from the basket (measured in the horizontal direction) must he start his jump to reach his maximum height at the same time as he reaches the basket?
Solution: (a) 3.84 m/s; (b) 1.96 m - A football player punts the ball at a 45.0º angle. Without an effect from the wind, the ball would travel 60.0 m horizontally.
(a) What is the initial speed of the ball?
(b) When the ball is near its maximum height it experiences a brief gust of wind that reduces its horizontal velocity by 1.50 m/s. What distance does the ball travel horizontally?
Solution: (a) 24.2 m/s; (b) The ball travels a total of 57.4 m with the brief gust of wind. - Prove that the trajectory of a projectile is parabolic, having the form [latex]y=\text{ax}+{\text{bx}}^{2}[/latex]. To obtain this expression, solve the equation [latex]x={v}_{0x}t[/latex] for [latex]t[/latex] and substitute it into the expression for [latex]y={v}_{0y}t–\left(1/2\right){\text{gt}}^{2}[/latex] (These equations describe the [latex]x[/latex] and [latex]y[/latex] positions of a projectile that starts at the origin.) You should obtain an equation of the form [latex]y=\text{ax}+{\text{bx}}^{2}[/latex] where [latex]a[/latex] and [latex]b[/latex] are constants.
- Construct Your Own Problem: Consider a ball tossed over a fence.
Construct a problem in which you calculate the ball’s needed initial velocity to just clear the fence. Among the things to determine are; the height of the fence, the distance to the fence from the point of release of the ball, and the height at which the ball is released. You should also consider whether it is possible to choose the initial speed for the ball and just calculate the angle at which it is thrown. Also examine the possibility of multiple solutions given the distances and heights you have chosen.
