Chapter 2: Describing Movement in One Dimension, 1-D Linear Kinematics
Problems & Exercises
2.1 Displacement
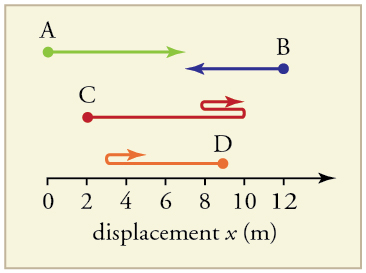
- Find the following for path A in Figure 2.57:
(a) The distance traveled.
(b) The magnitude of the displacement from start to finish.
(c) The displacement from start to finish.
Solution: (a) 7 m; (b) 7 m; (c) (+7 m) - Find the following for path B in Figure 2.57:
(a) The distance traveled.
(b) The magnitude of the displacement from start to finish.
(c) The displacement from start to finish. - Find the following for path C in Figure 2.57:
(a) The distance traveled.
(b) The magnitude of the displacement from start to finish.
(c) The displacement from start to finish.
Solution: a) 8m + 2 m + 3 m = 12 m; b) 8 m; c) Δx = 11 m – 2 m = +9 m - Find the following for path D in Figure 2.57:
(a) The distance traveled.
(b) The magnitude of the displacement from start to finish.
(c) The displacement from start to finish
2.2 Vectors, Scalars, and Coordinate Systems
- *A scuba diver makes a slow descent into the depths of the ocean. His vertical position with respect to a boat on the surface changes several times. He makes the first stop 9.0 m from the boat but has a problem with equalizing the pressure, so he ascends 3.0 m and then continues descending for another 12.0 m to the second stop. From there, he ascends 4 m and then descends for 18.0 m, ascends again for 7 m and descends again for 24.0 m, where he makes a stop, waiting for his buddy.
(a) Assuming the positive direction up to the surface, express his net vertical displacement vector in terms of the unit vector.
(b)What is his distance to the boat?
Solution: (a) h =−49m; (b) 49 m - *In a tug-of-war game on one campus, 15 students pull on a rope at both ends in an effort to displace the central knot to one side or the other. Two students pull with force 196 N each to the right, four students pull with force 98 N each to the left, five students pull with force 62 N each to the left, three students pull with force 150 N each to the right, and one student pulls with force 250 N to the left.
(a) Assuming the positive direction to the right, express the net pull on the knot in terms of the unit vector.
(b)How big is the net pull on the knot? In what direction? - *Suppose you walk 18.0 m straight west and then 25.0 m straight north. How far are you from your starting point and what is the compass direction of a line connecting your starting point to your final position? Use a graphical method.
Solution: 30.8 m, 35.7° west of north - *For the vectors given in the following figure, use a graphical method to find the following resultants:
(a) A +B
(b) C + B
(c) D + F
(d) A - B
(e) D - F
(f) A + 2F
(g) C- 2D + 3F
(h) A - 4D + 2F - *A delivery man starts at the post office, drives 40 km north, then 20 km west, then 60 km northeast, and finally 50 km north to stop for lunch. Use a graphical method to find his net displacement vector.
Solution: 134 km, 80° - *An adventurous dog strays from home, runs three blocks east, two blocks north, one block east, one block north, and two blocks west. Assuming that each block is about 100 m, how far from home and in what direction is the dog? Use a graphical method.
- *In an attempt to escape a desert island, a castaway builds a raft and sets out to sea. The wind shifts a great deal during the day and he is blown along the following directions: 2.50 km and
south of east, then 1.30 km and 25.0° south of west, then 5.10 km straight east, then 1.70 km and 5.00° east of north, then 7.20 km and 55.0°south of west, and finally 2.80 km and
north of east. Use a graphical method to find the castaway’s final position relative to the island.Solution: 7.34 km, 63.5° south of east
- *A surveyor measures the distance across a river that flows straight north by the following method. Starting directly across from a tree on the opposite bank, the surveyor walks 100 m along the river to establish a baseline. She then sights across to the tree and reads that the angle from the baseline to the tree is
. How wide is the river?
- *A pedestrian walks 6.0 km east and then 13.0 km north. Use a graphical method to find the pedestrian’s resultant displacement and geographic direction.
Solution: 14.3 km, 65° - *Suppose you walk 18.0 m straight west and then 25.0 m straight north.
(a) How far are you from your starting point?
(b) What is your displacement vector?
(c)What is the direction of your displacement? Assume the +x-axis is to the east. - *A barge is pulled by the two tugboats shown in the following figure. One tugboat pulls on the barge with a force of magnitude 4000 units of force at 15° above the line AB (see the figure and the other tugboat pulls on the barge with a force of magnitude 5000 units of force at 12° below the line AB. Resolve the pulling forces to their scalar components and find the components of the resultant force pulling on the barge.
(a) What is the magnitude of the resultant pull?
(b)What is its direction relative to the line AB?
- *You fly 32.0km in a straight line in still air in the direction 35.0° south of west.
(a) Find the distances you would have to fly due south and then due west to arrive at the same point.
(b) Find the distances you would have to fly first in a directionsouth of west and then in a direction 45.0° west of north. Note these are the components of the displacement along a different set of axes—namely, the one rotated by 45° with respect to the axes in (a).Solution: (a) 18.4 km and 26.2 km; (b) 31.5 km and 5.56 km
- *A skater glides along a circular path of radius 5.00 m in clockwise direction. When he coasts around one-half of the circle, starting from the west point, find
(a) the magnitude of his displacement vector and
(b) how far he actually skated.
(c) What is the magnitude of his displacement vector when he skates all the way around the circle and comes back to the west point?
Solution: (a) 10.00 m; (b) 5π; (c) 0 - *A diver explores a shallow reef off the coast of Belize. She initially swims 90.0 m north, makes a turn to the east and continues for 200.0 m, then follows a big grouper for 80.0 m in the direction 30° north of east. In the meantime, a local current displaces her by 150.0 m south. Assuming the current is no longer present, in what direction and how far should she now swim to come back to the point where she started?
Solution: 270 m,north of west
2.3 Time, Velocity, and Speed
- A helicopter blade spins at exactly 100 revolutions per minute. Its tip is 5.00 m from the center of rotation.
(a) Calculate the average speed of the blade tip in the helicopter’s frame of reference.
(b) What is its average velocity over one revolution? - The North American and European continents are moving apart at a rate of about 3 cm/y. At this rate how long will it take them to drift 500 km farther apart than they are at present?
Solution: [latex]2×{\text{10}}^{7}\phantom{\rule{0.25em}{0ex}}\text{years}[/latex] - A student drove to the university from her home and noted that the odometer reading of her car increased by 12.0 km. The trip took 18.0 min.
(a) What was her average speed?
(b) If the straight-line distance from her home to the university is 10.3 km in a direction [latex]\text{25}\text{.}0º[/latex] south of east, what was her average velocity?
(c) If she returned home by the same path 7 h 30 min after she left, what were her average speed and velocity for the entire trip?
Solution: (a) [latex]\text{40}\text{.}\text{0 km/h}[/latex]; (b) 34.3 km/h, [latex]\text{25º}\phantom{\rule{0.25em}{0ex}}\text{S of E}\text{.}[/latex]; (c) [latex]\text{average speed}=\text{3.20 km/h,}\phantom{\rule{0.25em}{0ex}}\stackrel{-}{v}=0.[/latex] - The speed of propagation of the action potential (an electrical signal) in a nerve cell depends (inversely) on the diameter of the axon (nerve fiber). If the nerve cell connecting the spinal cord to your feet is 1.1 m long, and the nerve impulse speed is 18 m/s, how long does it take for the nerve signal to travel this distance?
- Conversations with astronauts on the lunar surface were characterized by a kind of echo in which the earthbound person’s voice was so loud in the astronaut’s space helmet that it was picked up by the astronaut’s microphone and transmitted back to Earth. It is reasonable to assume that the echo time equals the time necessary for the radio wave to travel from the Earth to the Moon and back (that is, neglecting any time delays in the electronic equipment). Calculate the distance from Earth to the Moon given that the echo time was 2.56 s and that radio waves travel at the speed of light [latex]\left(3\text{.}\text{00}×{\text{10}}^{8}\phantom{\rule{0.25em}{0ex}}\text{m/s}\right)[/latex].
Solution: 384,000 km - A football quarterback runs 15.0 m straight down the playing field in 2.50 s. He is then hit and pushed 3.00 m straight backward in 1.75 s. He breaks the tackle and runs straight forward another 21.0 m in 5.20 s. Calculate his average velocity:
(a) for each of the three intervals and
(b) for the entire motion. - *Professional baseball player Nolan Ryan could pitch a baseball at approximately 160.0 km/h. At that average velocity, how long did it take a ball thrown by Ryan to reach home plate, which is 18.4 m from the pitcher’s mound? Compare this with the average reaction time of a human to a visual stimulus, which is 0.25 s.
- *In a 100-m race, the winner is timed at 11.2 s. The second-place finisher’s time is 11.6 s. How far is the second-place finisher behind the winner when she crosses the finish line? Assume the velocity of each runner is constant throughout the race.
- *A cyclist sprints at the end of a race to clinch a victory. She has an initial velocity of 11.5 m/s and accelerates at a rate of 0.500 m/s2 for 7.00 s.
(a) What is her final velocity?
(b) The cyclist continues at this velocity to the finish line. If she is 300 m from the finish line when she starts to accelerate, how much time did she save?
(c) The second-place winner was 5.00 m ahead when the winner started to accelerate, but he was unable to accelerate, and traveled at 11.8 m/s until the finish line. What was the difference in finish time in seconds between the winner and runner-up? How far back was the runner-up when the winner crossed the finish line? - *A cyclist rides 8.0 km east for 20 minutes, then he turns and heads west for 8 minutes and 3.2 km. Finally, he rides east for 16 km, which takes 40 minutes.
(a) What is the final displacement of the cyclist?
(b) What is his average velocity? - %A biker completes a 10 km course in 53 min. What was her average velocity in m/s?
Solution: 3.1 m/s - %A swimmer completes the first 2 laps of a 400m freestyle race in 40 seconds, the next 150m is swam at a constant speed and completed in 111 seconds. The last half of the race has times of 42 seconds, 44 seconds, 45 seconds and 41 seconds for each 50m interval. Assume pool length is 25m.
(a) What is their average pace for the first 50m of the race, as well as the entire race?
(b) What was the fastest pace achieved during the swim?
(c) Quantify the variance in their pace by:
(i) average variance (per 50m section)
(ii) max variance
(iii) count
d) Bonus: what type of pacing profile did they follow?
Solution: (a) 1:20/100m and 1:20.8/100m (or 1:21/100m rounded to nearest second); (b) 1:14/100m (in the 111 second section); (c) (i) average variance of 2.63 seconds in each 50m section (or 5.3 seconds/100m if representing as pace, or 6.5% as relative), (ii) max variance: 4.6 seconds in second last 50m (9.2 seconds/100m or 11.5%), (iii) counts: 2 ‘periods’ of pace variation; or alternatively 6 total intervals were above or below the average pace
2.4 Acceleration
- A cheetah can accelerate from rest to a speed of 30.0 m/s in 7.00 s. What is its acceleration?
Solution: [latex]4\text{.}\text{29}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}[/latex] - Professional Application
Dr. John Paul Stapp was U.S. Air Force officer who studied the effects of extreme deceleration on the human body. On December 10, 1954, Stapp rode a rocket sled, accelerating from rest to a top speed of 282 m/s (1015 km/h) in 5.00 s, and was brought jarringly back to rest in only 1.40 s! Calculate his:
(a) acceleration and
(b) deceleration. Express each in multiples of [latex]g[/latex] [latex]\left(9\text{.}\text{80 m}{\text{/s}}^{2}\right)[/latex] by taking its ratio to the acceleration of gravity. - A commuter backs her car out of her garage with an acceleration of [latex]1\text{.}{\text{40 m/s}}^{2}[/latex].
(a) How long does it take her to reach a speed of 2.00 m/s?
(b) If she then brakes to a stop in 0.800 s, what is her deceleration?
Solution: (a) [latex]1\text{.}\text{43 s}[/latex]; (b) [latex]-2\text{.}\text{50}\phantom{\rule{0.25em}{0ex}}{\text{m/s}}^{2}[/latex] - *A cyclist travels from point A to point B in 10 min. During the first 2.0 min of her trip, she maintains a uniform acceleration of 0.090m/s2. She then travels at constant velocity for the next 5.0 min. Next, she accelerates opposite to the motion at a constant rate so that she comes to a rest at point B 3.0 min later.
(a) Sketch the velocity-versus-time graph for the trip.
(b) What is the acceleration during the last 3 min?
(c) How far does the cyclist travel? - *Pablo is running in a half marathon at a velocity of 3 m/s. Another runner, Jacob, is 50 meters behind Pablo with the same velocity. Jacob begins to accelerate at 0.05 m/s2.
(a) How long does it take Jacob to catch Pablo?
(b) What is the distance covered by Jacob?
(c) What is the final velocity of Jacob? - %a) A car travels 500 m in 26 seconds. What is it’s average velocity?
b) The car then comes to a stop light and stops in 3 sec. What was its acceleration?
Solution: (a) 19.2 m/s; (b) 6.4 m/s2 - %A cyclist is descending a mountain at 19.4 m/s and needs to slow down to 13.8 m/s to avoid going over the cliff. If the cyclist’s brakes slow him down at a rate of -1.5 m/s2 , how much time does he need to avoid the cliff?
Solution: 3.7 s - %A runner accelerates 0.2 m/s2 in the last 20 seconds of the race. If his initial velocity was 5 m/s, what is his velocity at the finish line?
Solution: 9 m/s
2.5 Motion with Constant Acceleration
-
An Olympic-class sprinter starts a race with an acceleration of 4.50m/s2.
(a) What is her speed 2.40 s later?
(b) Sketch a graph of her position vs. time for this period.
Solution: (a) 10.8 m/s - A well-thrown ball is caught in a well-padded mitt. If the acceleration of the ball is 2.10×104m/s2, and 1.85 ms (1ms=10−3s) elapses from the time the ball first touches the mitt until it stops, what is the initial velocity of the ball
Solution: 38.9 m/s - At the end of a race, a runner decelerates from a velocity of 9.00 m/s at a rate of 2.00m/s2.
(a) How far does she travel in the next 5.00 s?
(b) What is her final velocity?
(c) Evaluate the result. Does it make sense?
Solution: (a) 20m; (b) -1.0m/s; (c) Not really, although the calculations are correct, they imply the runner would continue slowing down until they switched directions, rather than coming to a stop. This might be interpreted as them walking back towards the finish line, but it's more reasonable to assume most runners would stop for a few seconds after crossing the finish line. - Blood is accelerated from rest to 30.0 cm/s in a distance of 1.80 cm by the left ventricle of the heart.
(a) Make a sketch of the situation.
(b) List the knowns in this problem.
(c) How long does the acceleration take? To solve this part, first identify the unknown, then discuss how you chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, checking your units.
(d) Is the answer reasonable when compared with the time for a heartbeat?
Solution:(b) knowns: 𝑣=30.0cm/s, 𝑥=1.80cm; (c) 𝑎=250cm/s2, 𝑡=0.12s; (d) yes - During a slap shot, a hockey player accelerates the puck from a velocity of 8.00 m/s to 40.0 m/s in the same direction. If this shot takes 3.33×10−2s, what is the distance over which the puck accelerates?
Solution: The acceleration is 960 m/s2 and so the distance is 0.799 m - An unwary football player collides with a padded goalpost while running at a velocity of 7.50 m/s and comes to a full stop after compressing the padding and his body 0.350 m.
(a) What is his acceleration?
(b) How long does the collision last? - In World War II, there were several reported cases of airmen who jumped from their flaming airplanes with no parachute to escape certain death. Some fell about 20,000 feet (6000 m), and some of them survived, with few life-threatening injuries. For these lucky pilots, the tree branches and snow drifts on the ground allowed their deceleration to be relatively small. If we assume that a pilot’s speed upon impact was 123 mph (54 m/s), then what was his deceleration? Assume that the trees and snow stopped him over a distance of 3.0 m.
- A bicycle racer sprints at the end of a race to clinch a victory. The racer has an initial velocity of 11.5 m/s and accelerates at the rate of for 7.00 s.
(a) What is his final velocity?
(b) The racer continues at this velocity to the finish line. If he was 300 m from the finish line when he started to accelerate, how much time did he save?
(c) One other racer was 5.00 m ahead when the winner started to accelerate, but he was unable to accelerate, and traveled at 11.8 m/s until the finish line. How far ahead of him (in meters and in seconds) did the winner finish? - (a) A world record was set for the men’s 100-m dash in the 2008 Olympic Games in Beijing by Usain Bolt of Jamaica. Bolt “coasted” across the finish line with a time of 9.69 s. If we assume that Bolt accelerated for 3.00 s to reach his maximum speed, and maintained that speed for the rest of the race, calculate his maximum speed and his acceleration.
(b) During the same Olympics, Bolt also set the world record in the 200-m dash with a time of 19.30 s. Using the same assumptions as for the 100-m dash, what was his maximum speed for this race?
2.7 Falling Objects: Human Movement in the Vertical Direction
Assume air resistance is negligible unless otherwise stated.
- Calculate the displacement and velocity at times of
(a) 0.500,
(b) 1.00,
(c) 1.50, and
(d) 2.00 s
for a ball thrown straight up with an initial velocity of 15.0 m/s. Take the point of release to be [latex]{y}_{0}=0[/latex].
Solution:(a) [latex]{y}_{1}=6\text{.}\text{28 m} \text; {v}_{1}=\text{10}\text{.}\text{1 m/s}[/latex]; (b) [latex]{y}_{2}=\text{10}\text{.}\text{1 m} \text; {v}_{2}=5\text{.}\text{20 m/s}[/latex]; (c) [latex]{y}_{3}=11\text{.}5 m \text; {v}_{3}=0\text{.300 m/s}[/latex], (d) [latex]{y}_{4}=10\text{.4 m} \text; {v}_{4}=-4\text{.60 m/s}[/latex] - Calculate the displacement and velocity at times of
(a) 0.500,
(b) 1.00,
(c) 1.50,
(d) 2.00, and
(e) 2.50 s
for a rock thrown straight down with an initial velocity of 14.0 m/s from the Verrazano Narrows Bridge in New York City. The roadway of this bridge is 70.0 m above the water. - A basketball referee tosses the ball straight up for the starting tip-off. At what velocity must a basketball player leave the ground to rise 1.25 m above the floor in an attempt to get the ball?
Solution: [latex]{v}_{0}=4\text{.}\text{95 m/s}[/latex] - A rescue helicopter is hovering over a person whose boat has sunk. One of the rescuers throws a life preserver straight down to the victim with an initial velocity of 1.40 m/s and observes that it takes 1.8 s to reach the water.
(a) List the knowns in this problem.
(b) How high above the water was the preserver released? Note that the downdraft of the helicopter reduces the effects of air resistance on the falling life preserver, so that an acceleration equal to that of gravity is reasonable. - *A diver bounces straight up from a diving board and falls feet first into a pool. She starts with a velocity of 4.00 m/s, and her takeoff point is 1.80 m above the pool.
(a) How long are her feet in the air?
(b) What is her highest point above the board?
(c) What is her velocity when her feet hit the water? - A very strong, but inept, shot putter puts the shot straight up vertically with an initial velocity of 11.0 m/s. How long does he have to get out of the way if the shot was released at a height of 2.20 m, and he is 1.80 m tall?
- You throw a ball straight up with an initial velocity of 15.0 m/s. It passes a tree branch on the way up at a height of 7.00 m. How much additional time will pass before the ball passes the tree branch on the way back down?
Solution: 1.91 s - An object is dropped from a height of 75.0 m above ground level.
(a) Determine the distance traveled during the first second.
(b) Determine the final velocity at which the object hits the ground.
(c) Determine the distance traveled during the last second of motion before hitting the ground. - A ball is thrown straight up. It passes a 2.00-m-high window 7.50 m off the ground on its path up and takes 0.312 s to go past the window. What was the ball’s initial velocity? Hint: First consider only the distance along the window, and solve for the ball's velocity at the bottom of the window. Next, consider only the distance from the ground to the bottom of the window, and solve for the initial velocity using the velocity at the bottom of the window as the final velocity.
- Suppose you drop a rock into a dark well and, using precision equipment, you measure the time for the sound of a splash to return.
(a) Neglecting the time required for sound to travel up the well, calculate the distance to the water if the sound returns in 2.0000 s.
(b) Now calculate the distance taking into account the time for sound to travel up the well. The speed of sound is 332.00 m/s in this well.
Solution: (a) [latex]\text{19}\text{.}\text{6 m}[/latex]; (b) [latex]\text{18}\text{.}\text{5 m}[/latex] - A soft tennis ball is dropped onto a hard floor from a height of 1.50 m and rebounds to a height of 1.10 m.
(a) Calculate its velocity just before it strikes the floor.
(b) Calculate its velocity just after it leaves the floor on its way back up.
(c) Calculate its acceleration during contact with the floor if that contact lasts 3.50 ms [latex]\left(3\text{.}\text{50}×{\text{10}}^{-3}\phantom{\rule{0.25em}{0ex}}\text{s}\right)[/latex].
(d) How much did the ball compress during its collision with the floor, assuming the floor is absolutely rigid?
Solution: (a) 𝑣=5.42m/s; (b) 𝑣=4.64m/s; (c) 𝑎=2874.28m/s2; (d) (𝑥−𝑥0)=5.11×10−3m - Compare the time in the air of a basketball player who jumps 1.0 m vertically off the floor with that of a player who jumps 0.3 m vertically.
Solution: 1.0 m = 0.9s; 0.3 m = 0.5s

