Chapter 2: Describing Movement in One Dimension, 1-D Linear Kinematics

2.4 Acceleration

Authors: Paul Peter Urone, Roger Hinrichs
Adapted by: Rob Pryce, Alix Blacklin

 

Learning Objectives

By the end of this section, you will be able to:

  • Define and distinguish between instantaneous and average acceleration.
  • Understand the effect of accelerations in different directions.
  • Calculate acceleration given initial time, initial velocity, final time, and final velocity.
a wheelchair athlete pushes hard on the wheels of their chair to accelerate forward
Figure 2.12 An athlete pushes hard to accelerate to a high speed. Their acceleration is in the same direction of their motion. (credit: Seth Kane, Unsplash)

In everyday conversation, to accelerate means to speed up. The accelerator in a car can in fact cause it to speed up. The greater the acceleration, the greater the change in velocity over a given time. Acceleration is defined as the rate of change of velocity.

Average acceleration can be calculated as:

[latex]\bar{a} = \frac {\Delta v}{\Delta t} = \frac {v_f-v_i}{t_f-t_i}[/latex]

where
[latex]\bar{a}[/latex] is average acceleration,
[latex]v[/latex] is velocity, and
[latex]t[/latex] is time.
(The bar over the a means ‘average’ acceleration)

Because acceleration is velocity in m/s divided by time in s, the SI units for acceleration are [latex]m/s^2[/latex], meters per second squared, or meters per second per second (m/s/s), which literally means by how many meters per second the velocity changes every second.

Recall that velocity is a vector—it has both magnitude and direction. This means that a change in velocity can be a change in magnitude (or speed), but it can also be a change in direction. For example, if a car turns a corner at constant speed, it is accelerating because its direction is changing. The quicker you turn, the greater the acceleration. So there is an acceleration when velocity changes either in magnitude (an increase or decrease in speed) or in direction, or both.

ACCELERATION AS A VECTOR

Acceleration is a vector in the same direction as the change in velocity, [latex]\Delta v[/latex]. Since velocity is a vector, it can change either in magnitude or in direction. Acceleration is therefore a change in either speed or direction, or both.

Keep in mind that although acceleration is in the direction of the change in velocity, it is not always in the direction of motion. When an object slows down, its acceleration is opposite to the direction of its motion. This is also known as deceleration.

a cyclist rides their bike down a snow covered hill in the winter time
Figure 2.13 A cyclist decelerates as they come to a stop at the bottom of the hill. They are accelerating in a direction opposite to their direction of motion. That is, their direction of motion is down the hill and their acceleration is opposite, or up the hill. (credit: Jonny Neuenhagen, Unsplash)

MISCONCEPTION ALERT: DECELERATION vs. NEGATIVE ACCELERATION

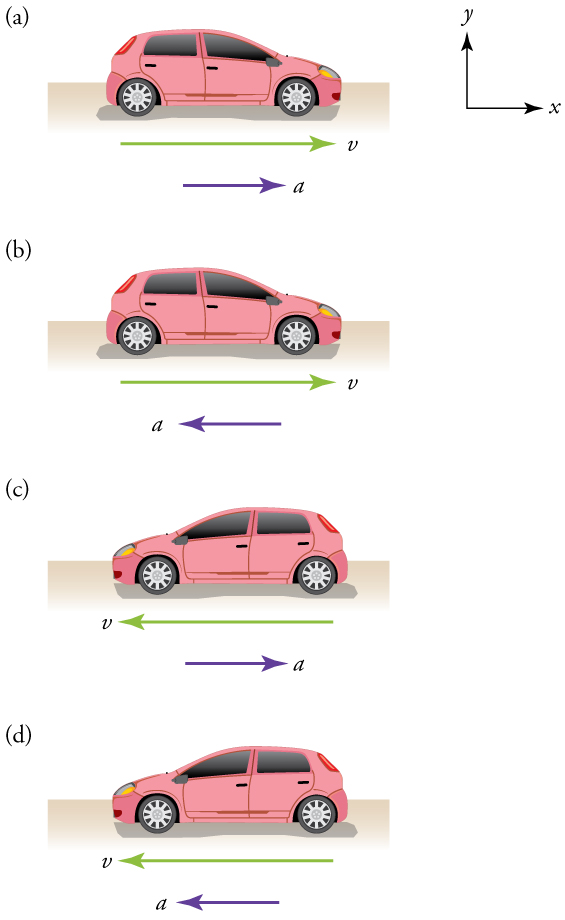
Deceleration always refers to acceleration in the direction opposite to the direction of the velocity. Deceleration always reduces speed. Negative acceleration, however, is acceleration in the negative direction in the chosen coordinate system. Negative acceleration may or may not be deceleration, and deceleration may or may not be considered negative acceleration. For example, consider Figure 2.14. Read the caption for an explanation of how the direction of the acceleration relates to the direction of motion.

 

Four separate diagrams of cars moving. Diagram a: A car moving toward the right. A velocity vector arrow points toward the right. An acceleration vector arrow also points toward the right. Diagram b: A car moving toward the right in the positive x direction. A velocity vector arrow points toward the right. An acceleration vector arrow points toward the left. Diagram c: A car moving toward the left. A velocity vector arrow points toward the left. An acceleration vector arrow points toward the right. Diagram d: A car moving toward the left. A velocity vector arrow points toward the left. An acceleration vector arrow also points toward the left.
Figure 2.14 (a) This car is speeding up as it moves toward the right. It therefore has positive acceleration in our coordinate system. (b) This car is slowing down as it moves toward the right. Therefore, it has negative acceleration in our coordinate system, because its acceleration is toward the left. The car is also decelerating: the direction of its acceleration is opposite to its direction of motion. (c) This car is moving toward the left, but slowing down over time. Therefore, its acceleration is positive in our coordinate system because it is toward the right. However, the car is decelerating because its acceleration is opposite to its motion. (d) This car is speeding up as it moves toward the left. It has negative acceleration because it is accelerating toward the left. However, because its acceleration is in the same direction as its motion, it is speeding up (not decelerating).

 

Example: Calculating Acceleration: A Cyclist Starts the Race

A cyclist coming out of the gate to start a race accelerates from rest to a velocity of 12.50 m/s due west in 3.50 s. What is their average acceleration?

a cyclist accelerates down the road
Figure 2.15 A cyclist sprints to start a race (credit: Garry Neesam, Unsplash)

Strategy

First we draw a sketch and assign a coordinate system to the problem. This is a simple problem, but it always helps to visualize it. Notice that we assign east as positive and west as negative. Thus, in this case, we have negative velocity.

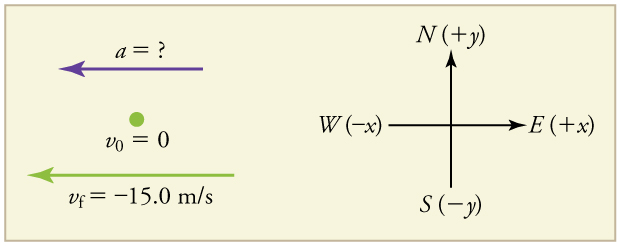
An acceleration vector arrow pointing west, in the negative x direction, labeled with a equals question mark. A velocity vector arrow also pointing toward the left, with initial velocity labeled as 0 and final velocity labeled as negative fifteen point 0 meters per second.
Figure 2.16 Frame of reference for cyclist at the beginning of a race

We can solve this problem by identifying [latex]\Delta v[/latex] and [latex]\Delta t[/latex] from the given information and then calculating the average acceleration directly from the equation  [latex]\bar{a} = \frac {\Delta v}{\Delta t} = \frac {v_f-v_i}{t_f-t_i}[/latex].

Solution

1. Identify the knowns. [latex]v_i = 0, v_f = -12.50 m/s[/latex] (the negative sign indicates direction toward the west), [latex]\Delta t = 3.50s[/latex].

2. Find the change in velocity. Since the rider is going from zero to -12.50 m/s, its change in velocity equals its final velocity: [latex]\Delta v = v_f = -12.50 m/s[/latex].

3. Plug in the known values ([latex]\Delta v[/latex] and [latex]\Delta t[/latex]) and solve for the unknown [latex]\bar{a}[/latex].
[latex]\bar{a} = \frac {\Delta v} {\Delta t} = \frac {-12.50m/s} {3.50s} = -3.57 m/s^2[/latex]

Discussion

The negative sign for acceleration indicates that acceleration is toward the west. An acceleration of 3.57 [latex]m/s^2[/latex] due west means that the rider increases its velocity by 3.57 m/s due west each second, that is, 3.57 meters per second per second, which we write as 3.57 [latex]m/s^2[/latex]. This is truly an average acceleration, because the start is probably not smooth. Later we will learn how to estimate the force required to produce that acceleration.

Instantaneous Acceleration

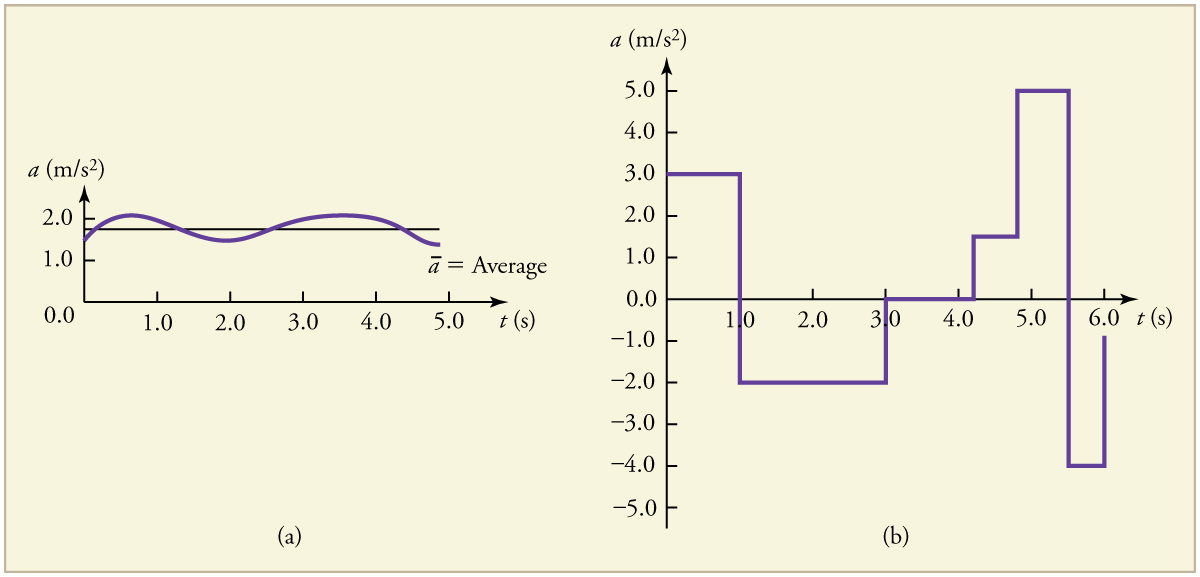
Instantaneous acceleration [latex]a[/latex], or the acceleration at a specific instant in time, is obtained by the same process as discussed for instantaneous velocity in the previous section—that is, by considering an infinitesimally small interval of time. How do we find instantaneous acceleration using only algebra? One answer is that we choose an average acceleration that is representative of the motion. Figure 2.17 shows graphs of instantaneous acceleration versus time for two very different motions. In (a), the acceleration varies slightly and the average over the entire interval is nearly the same as the instantaneous acceleration at any time. In this case, it would be reasonable to treat this motion as if it had a constant acceleration equal to the average (in this case about [latex]1.8 m/s^2[/latex]). In (b), the acceleration varies drastically over time. In these situations it is better to consider smaller time intervals and examine the average acceleration for each interval. For example, we could consider motion over the time intervals from 0 to 1.0 s and from 1.0 to 3.0 s as separate motions with accelerations of [latex]+3.0 m/s^2[/latex] and [latex]-2.0 m/s^2[/latex], respectively.

Line graphs of instantaneous acceleration in meters per second per second versus time in seconds. The line on graph (a) shows slight variation above and below an average acceleration of about 1 point 8 meters per second per second. The line on graph (b) shows great variation over time, with instantaneous acceleration constant at 3 point 0 meters per second per second for 1 second, then dropping to negative 2 point 0 meters per second per second for the next 2 seconds, and then rising again, and so forth.
Figure 2.17 Graphs of instantaneous acceleration versus time for two different one-dimensional motions. (a) Here acceleration varies only slightly and is always in the same direction, since it is positive. The average over the interval is nearly the same as the acceleration at any given time. (b) Here the acceleration varies greatly, perhaps representing a package on a post office conveyor belt that is accelerated forward and backward as it bumps along. It is necessary to consider small time intervals (such as from 0 to 1.0 s) with constant or nearly constant acceleration in such a situation.

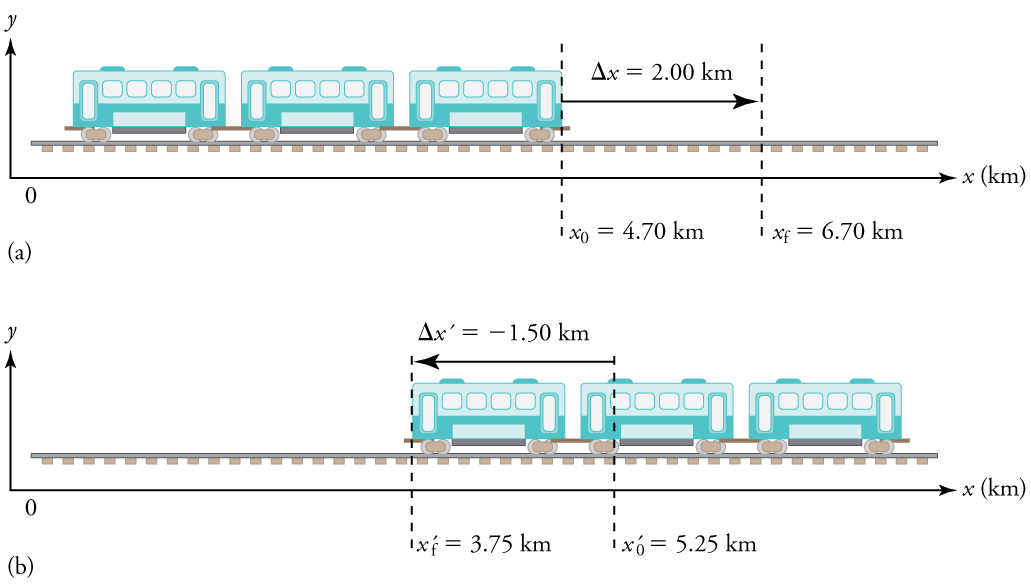
The next several examples consider the motion of the subway train shown in Figure 2.18. In (a) the train moves to the right, and in (b) it moves to the left. The examples are designed to further illustrate aspects of motion and some of the reasoning that goes into solving problems.

In part (a), a subway train moves from left to right from an initial position of x equals 4 point 7 kilometers to a final position of x equals 6 point 7 kilometers, with a displacement of 2 point 0 kilometers. In part (b), the train moves toward the left, from an initial position of 5 point 25 kilometers to a final position of 3 point 75 kilometers.
Figure 2.18 One-dimensional motion of a subway train considered in Examples 2.2 to 2.7. Here we have chosen the x-axis so that + means to the right and ‘-‘ means to the left for displacements, velocities, and accelerations. (a) The subway train moves to the right from with a displacement of +2.0 km. (b) The train moves to the left from with a displacement of -1.5 km. (Note that the prime symbol (′) is used simply to distinguish between displacement in the two different situations. The distances of travel and the size of the cars are on different scales to fit everything into the diagram.)

Example: Calculating Displacement: A Subway Train

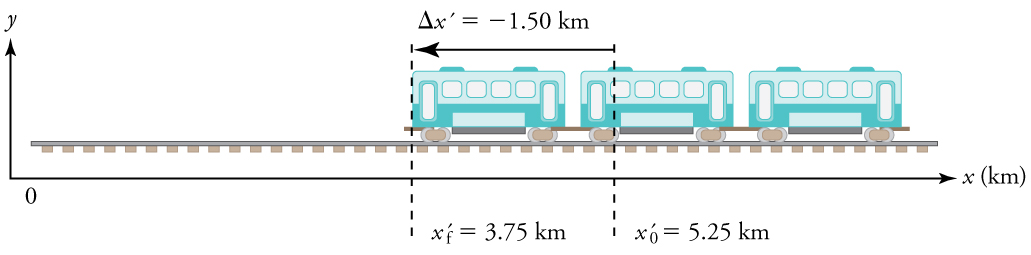
What are the magnitude and sign of displacements for the motions of the subway train shown in parts (a) and (b) of Figure 2.18?

Strategy

A drawing with a coordinate system is already provided, so we don’t need to make a sketch, but we should analyze it to make sure we understand what it is showing. Pay particular attention to the coordinate system. To find displacement, we use the equation [latex]\Delta x = x_f - x_i[/latex]. This is straightforward since the initial and final positions are given.

Solution

1. Identify the knowns. In the figure we see that for part a):

[latex]x_f = 6.70 km[/latex] and [latex]x_i = 4.70 km[/latex],

and for part b):

[latex]{x\prime}_f = 3.75 km[/latex] and [latex]{x\prime}_i = 5.25 km[/latex].

2. Solve for displacement in part (a).

[latex]\Delta x = x_f - x_i = \text {6.70 km} - \text {4.70 km} = +\text{2.00 km}[/latex]

3. Solve for displacement in part (b).

[latex]\Delta x\prime ={x\prime }_{f}-{x\prime }_{0}=\text{3.75 km}-\text{5.25 km}=-\text{1.50 km}[/latex]

Discussion

The direction of the motion in (a) is to the right and therefore its displacement has a positive sign, whereas motion in (b) is to the left and thus has a negative sign.

Example: Comparing Distance Traveled with Displacement: A Subway Train

What are the distances traveled for the motions shown in parts (a) and (b) of the subway train in Figure 2.18?

Strategy

To answer this question, think about the definitions of distance and distance traveled, and how they are related to displacement. Distance between two positions is defined to be the magnitude of displacement, which was found in Example 2.2. Distance traveled is the total length of the path traveled between the two positions. In the case of the subway train shown in Figure 2.18, the distance traveled is the same as the distance between the initial and final positions of the train.

Solution

1. The displacement for part (a) was +2.00 km. Therefore, the distance between the initial and final positions was 2.00 km, and the distance traveled was 2.00 km.

2. The displacement for part (b) was -1.50 km. Therefore, the distance between the initial and final positions was 1.50 km, and the distance traveled was 1.50 km.

Discussion

Distance is a scalar. It has magnitude but no sign to indicate direction.

Example: Calculating Acceleration: A Subway Train Speeding Up

Suppose the train in 2.18 (a) accelerates from rest to 30.0 km/h in the first 20.0 s of its motion. What is its average acceleration during that time interval?

Strategy

It is worth it at this point to make a simple sketch:

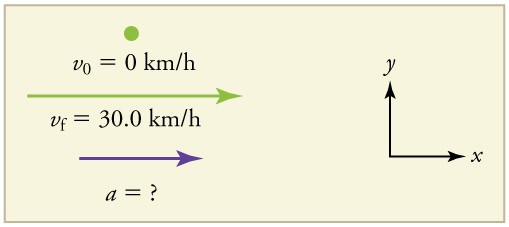
A point represents the initial velocity of 0 kilometers per second. Below the point is a velocity vector arrow pointing to the right, representing the final velocity of thirty point zero kilometers per hour. Below the velocity vector is an acceleration vector arrow labeled a equals question mark.
Figure 2.19 Frame of reference for accelerating subway train

This problem involves three steps. First we must determine the change in velocity, then we must determine the change in time, and finally we use these values to calculate the acceleration.

Solution

1. Identify the knowns:
[latex]{v}_{i}=0[/latex] (the trains starts at rest),
[latex]{v}_{f}=\text{30}\text{.}\text{0 km/h}[/latex], and
[latex]\Delta t=\text{20}\text{.}\text{0 s}[/latex].

2. Calculate [latex]\Delta v[/latex]. Since the train starts from rest, its change in velocity is [latex]\Delta v\text{=}\phantom{\rule{0.20em}{0ex}}\text{+}\text{30.0 km/h}[/latex], where the plus sign means velocity to the right.

3. Plug in known values and solve for the unknown, [latex]\bar{a}[/latex].

[latex]\bar{a}=\frac{\Delta v}{\Delta t}=\frac{+\text{30.0 km/h}}{\text{20}\text{.}0 s}[/latex]

4. Since the units are mixed (we have both hours and seconds for time), we need to convert everything into SI units of meters and seconds. (See Physical Quantities and Units for  more guidance.)

[latex]\bar{a}=\left(\frac{+\text{30 km/h}}{\text{20.0 s}}\right)\left(\frac{{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{m}}{\text{1 km}}\right)\left(\frac{\text{1 h}}{\text{3600 s}}\right)=0\text{.}{\text{417 m/s}}^{2}[/latex]

Discussion

The plus sign means that acceleration is to the right. This is reasonable because the train starts from rest and ends up with a velocity to the right (also positive). So acceleration is in the same direction as the change in velocity, as is always the case.

Example: Calculate Acceleration: A Subway Train Slowing Down

Now suppose that at the end of its trip, the train in Figure 2.18(a) slows to a stop from a speed of 30.0 km/h in 8.00 s. What is its average acceleration while stopping?

Strategy

A velocity vector arrow pointing toward the right with initial velocity of thirty point zero kilometers per hour and final velocity of 0. An acceleration vector arrow pointing toward the left, labeled a equals question mark.
Figure 2.20 Frame of reference for a subway train slowing down

In this case, the train is decelerating and its acceleration is negative because it is toward the left. As in the previous example, we must find the change in velocity and the change in time and then solve for acceleration.

Solution

1. Identify the knowns.
[latex]v_i=\text{30}\text{.0 km/h}[/latex],
[latex]v_f=0 km/h[/latex] (the train is stopped, so its velocity is 0), and
[latex]\Delta t=\text{8.00 s}[/latex].

2. Solve for the change in velocity, [latex]\Delta v[/latex].

[latex]\Delta v=v_f-v_i=0-\text{30}\text{.}\text{0 km/h}=-\text{30}\text{.0 km/h}[/latex]

3. Plug in the knowns, [latex]\Delta v[/latex] and [latex]\Delta t[/latex], and solve for [latex]\bar {a}[/latex].

[latex]\bar{a}=\frac{\Delta v}{\Delta t}=\frac{-\text{30}\text{.}\text{0 km/h}}{8\text{.}\text{00 s}}[/latex])

4. Convert the units to meters and seconds.

[latex]\bar{a}=\frac{\Delta v}{\Delta t}=\left(\frac{-\text{30.0 km/h}}{\text{8.00 s}}\right)\left(\frac{{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}\text{m}}{\text{1 km}}\right)\left(\frac{\text{1 h}}{\text{3600 s}}\right)={\text{−1.04 m/s}}^{2}\text{.}[/latex]

Discussion

The minus sign indicates that acceleration is to the left. This sign is reasonable because the train initially has a positive velocity in this problem, and a negative acceleration would oppose the motion. Again, acceleration is in the same direction as the change in velocity, which is negative here. This acceleration can be called a deceleration because it has a direction opposite to the velocity. 

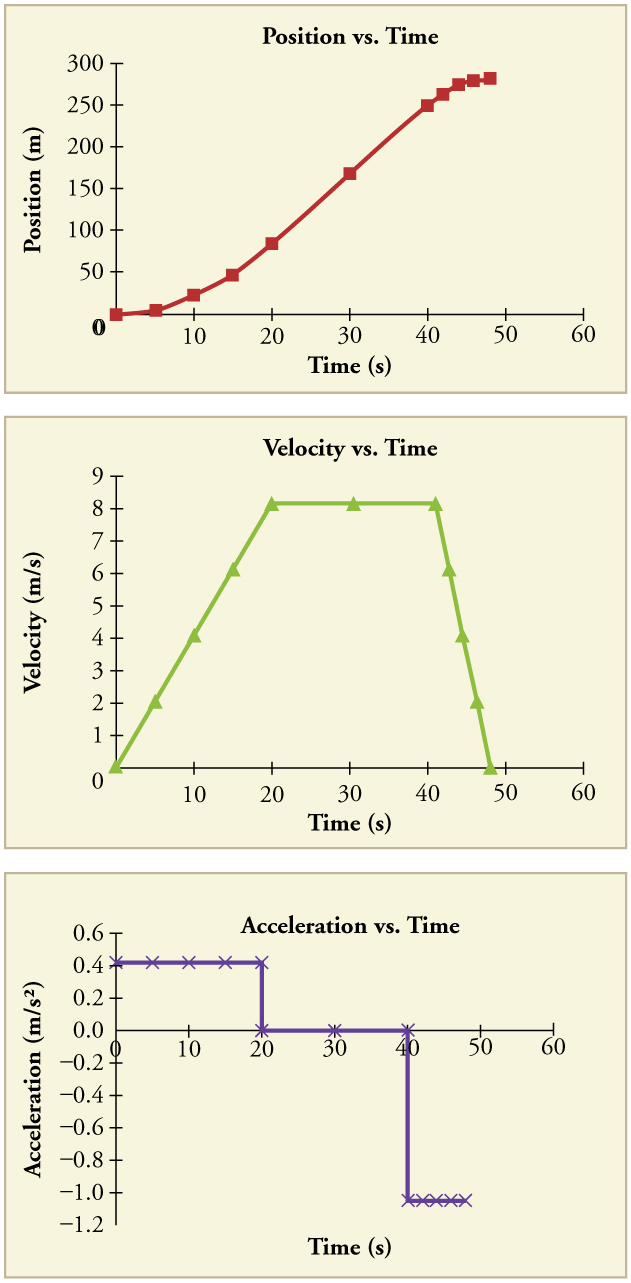
Graphing Position, Velocity, Acceleration

The graphs of position, velocity, and acceleration vs. time for the trains in Example 2.4 and Example 2.5 are displayed in Figure 2.21. (We have taken the velocity to remain constant from 20 to 40 s, after which the train decelerates.)

Three graphs. The first is a line graph of position in meters versus time in seconds. The line begins at the origin and has a concave up shape from time equals zero to time equals twenty seconds. It is straight with a positive slope from twenty seconds to forty seconds. It is then convex up from forty to fifty seconds. The second graph is a line graph of velocity in meters per second versus time in seconds. The line is straight with a positive slope beginning at the origin from 0 to twenty seconds. It is flat from twenty to forty seconds. From forty to fifty seconds the line is straight with a negative slope back down to a velocity of 0. The third graph is a line graph of acceleration in meters per second per second versus time in seconds. The line is flat with a positive constant acceleration from zero to twenty seconds. The line then drops to an acceleration of 0 from twenty to forty seconds. The line drops again to a negative acceleration from forty to fifty seconds.
Figure 2.21 (a) Position of the train over time. Notice that the train’s position changes slowly at the beginning of the journey, then more and more quickly as it picks up speed. Its position then changes more slowly as it slows down at the end of the journey. In the middle of the journey, while the velocity remains constant, the position changes at a constant rate. (b) Velocity of the train over time. The train’s velocity increases as it accelerates at the beginning of the journey. It remains the same in the middle of the journey (where there is no acceleration). It decreases as the train decelerates at the end of the journey. (c) The acceleration of the train over time. The train has positive acceleration as it speeds up at the beginning of the journey. It has no acceleration as it travels at constant velocity in the middle of the journey. Its acceleration is negative as it slows down at the end of the journey.

Example: Calculating Average Velocity: The Subway Train

What is the average velocity of the train in part b of Example 2.2, and shown again below, if it takes 5.00 min to make its trip?

The train moves toward the left, from an initial position of 5 point 25 kilometers to a final position of 3 point 75 kilometers.
Figure 2.22 A train travels 1.5km in 5:00 min

Strategy

Average velocity is displacement divided by time. It will be negative here, since the train moves to the left and has a negative displacement.

Solution

1. Identify the knowns.
[latex]{x\prime }_{f}=3\text{.75 km}[/latex],
[latex]{x\prime }_i=\text{5.25 km}[/latex],
[latex]\Delta t=\text{5.00 min}[/latex].

2. Determine displacement, [latex]\Delta x\prime[/latex]. We found [latex]\Delta x\prime[/latex] to be [latex]-\text{1.5 km}[/latex] in Example 2.2.

3. Solve for average velocity.

[latex]\bar{v}=\frac{\Delta x\prime }{\Delta t}=\frac{-\text{1.50 km}}{\text{5.00 min}}[/latex]

4. Convert units.

[latex]\bar{v}=\frac{\Delta x\prime }{\Delta t}=\left(\frac{-1\text{.}\text{50 km}}{5\text{.}\text{00 min}}\right)\left(\frac{\text{60 min}}{1 h}\right)=-\text{18}\text{.0 km/h}[/latex]

Discussion

The negative velocity indicates motion to the left.

Example: Calculating Deceleration: The Subway Train

Finally, suppose the train in Figure 2.22 slows to a stop from a velocity of 20.0 km/h in 10.0 s. What is its average acceleration?

Strategy

Once again, let’s draw a sketch:

A velocity vector arrow pointing to the left with initial velocity of negative twenty point 0 kilometers per hour and a final velocity of 0. An acceleration vector arrow pointing toward the right, labeled a equals question mark.
Figure 2.23 Reference frame for train slowing down in the negative direction.

As before, we must find the change in velocity and the change in time to calculate average acceleration.

Solution

1. Identify the knowns:
[latex]{v}_{0}=-\text{20 km/h}[/latex],
[latex]{v}_{f}=0 km/h[/latex],
[latex]\Delta t=\text{10}\text{.}0 s[/latex].

2. Calculate [latex]\Delta v[/latex]. The change in velocity here is actually positive, since

[latex]\Delta v = v_f - v_i = 0 - \left(-\text{20 km/h} \right) = + \text{20km/h}[/latex]

3. Solve for [latex]\bar{a}[/latex].

[latex]\bar{a}=\frac{\Delta v}{\Delta t}=\frac{+\text{20.0 km/h}}{\text{10.0 s}}[/latex]

4. Convert units.

[latex]\bar{a}=\left(\frac{+\text{20}\text{.}\text{0 km/h}}{\text{10}\text{.}\text{0 s}}\right)\left(\frac{{\text{10}}^{3}\phantom{\rule{0.25em}{0ex}}m}{1 km}\right)\left(\frac{1 h}{\text{3600 s}}\right)\text{=}\phantom{\rule{0.25em}{0ex}}\text{+}0\text{.556 m}{\text{/s}}^{2}[/latex]

Discussion

The plus sign means that acceleration is to the right. This is reasonable because the train initially has a negative velocity (to the left) in this problem and a positive acceleration opposes the motion (and so it is to the right). Again, acceleration is in the same direction as the change in velocity, which is positive here. As in Example 2.5, this acceleration can be called a deceleration since it is in the direction opposite to the velocity.

Sign and Direction

Perhaps the most important thing to note about these examples is the signs of the answers. In our chosen coordinate system, plus means the quantity is to the right and minus means it is to the left. This is easy to imagine for displacement and velocity. But it is a little less obvious for acceleration. Most people interpret negative acceleration as the slowing of an object. This was not the case in Example 2.7, where a positive acceleration slowed a negative velocity. The crucial distinction was that the acceleration was in the opposite direction from the velocity. In fact, a negative acceleration will increase a negative velocity. For example, the train moving to the left in Figure 2.22 is sped up by an acceleration to the left. In that case, both [latex]v[/latex] and [latex]a[/latex] are negative. The plus and minus signs give the directions of the accelerations. If acceleration has the same sign as the velocity, the object is speeding up. If acceleration has the opposite sign as the velocity, the object is slowing down.

Check Your Understanding

An airplane lands on a runway traveling east. Describe its acceleration.

Solution

If we take east to be positive, then the airplane has negative acceleration, as it is accelerating toward the west. It is also decelerating: its acceleration is opposite in direction to its velocity.

PhET Explorations: Moving Man Simulation

Learn about position, velocity, and acceleration graphs. Move the little man back and forth with the mouse and plot his motion. Set the position, velocity, or acceleration and let the simulation move the man for you.

https://phet.colorado.edu/en/simulations/moving-man

License

Icon for the Creative Commons Attribution 4.0 International License

Introduction to Biomechanics Copyright © 2022 by Rob Pryce is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book