Chapter 2: Describing Movement in One Dimension, 1-D Linear Kinematics
2.1 Displacement
Authors: Paul Peter Urone, Roger Hinrichs
Adapted by: Rob Pryce, Alix Blacklin
Learning Objectives
By the end of this section, you will be able to:
- Define position, displacement, distance, and distance traveled.
- Explain the relationship between position and displacement.
- Distinguish between displacement and distance traveled.
- Calculate the displacement and distance given initial position, final position, and the path between the two.

Position
In order to describe the motion of a person (or any object for that matter), you must first be able to describe their position—where they are at any particular time. More precisely, position is defined as the location in space relative to a specific reference frame. A reference frame is an arbitrary location (or origin) and set of axes from which the position and motion of an object can be described.
Earth is often used as a reference frame, and we often describe the position of a person or object as it relates to the Earth or to stationary objects in the Earth reference frame. For example, a high jumper's motion would be described in terms of the position of the person with respect to the Earth (or more specifically, the ground level they jumped from). While a professor’s position during a lecture could be described in terms of where she is in relation to the nearby white board (Figure 2.3).
In other cases, we use reference frames that are not stationary but are in motion relative to the Earth. To describe the position of a person in an airplane, for example, we use the airplane, not the Earth, as the reference frame (Figure 2.4). Or more commonly in biomechanics, we might describe the motion of one athlete with respect to another athlete - in this case, the reference is other athlete and we can calculate position, displacement or velocity of other athletes relative to them. That is, how far in front or behind they are, how quickly they are catching up or falling behind, and so on.
To describe the position of a person or object that is undergoing movement in 1-dimension (e.g. forwards or backwards), we often use the variable [latex]x[/latex], particularly if the motion is in the horizontal direction. In the next chapter, during the discussion of free fall, the variable [latex]y[/latex] will be used to describe motion in the vertical direction. In the next section we'll learn about axes in the reference frame.
Displacement
If an object moves relative to a reference frame (for example, if a professor moves to the right relative to a white board or a passenger moves toward the rear of an airplane), then the object’s position changes. This change in position is known as displacement. The word “displacement” implies that an object has moved, or has been displaced.
Displacement is calculated as:
[latex]\Delta x = x_f - x_i[/latex]
where
[latex]\Delta x[/latex] is displacement, and
[latex]x_f[/latex] is the final position, and
[latex]x_i[/latex] is the initial position.
In this text the upper case Greek letter [latex]\Delta[/latex] or delta always means “change in” whatever quantity follows it; thus, [latex]\Delta x[/latex] means change in position. Always solve for displacement by subtracting initial position [latex]x_i[/latex] from final position [latex]x_f[/latex].
Note that the SI unit for displacement is the meter (m) (see Physical Quantities and Units), but sometimes we'll encounter units of kilometers, miles, feet, and other units. Keep in mind that when non-SI units are used in a problem, you may need to convert them into SI-units (meters) when communicating with a scientific audience.
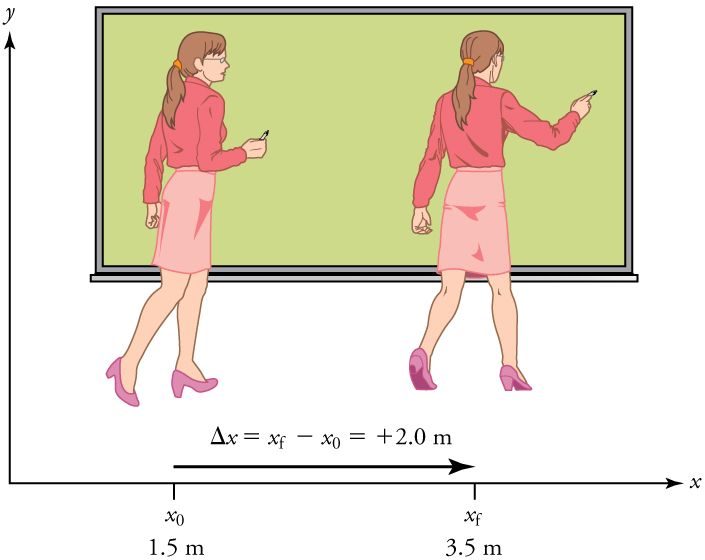
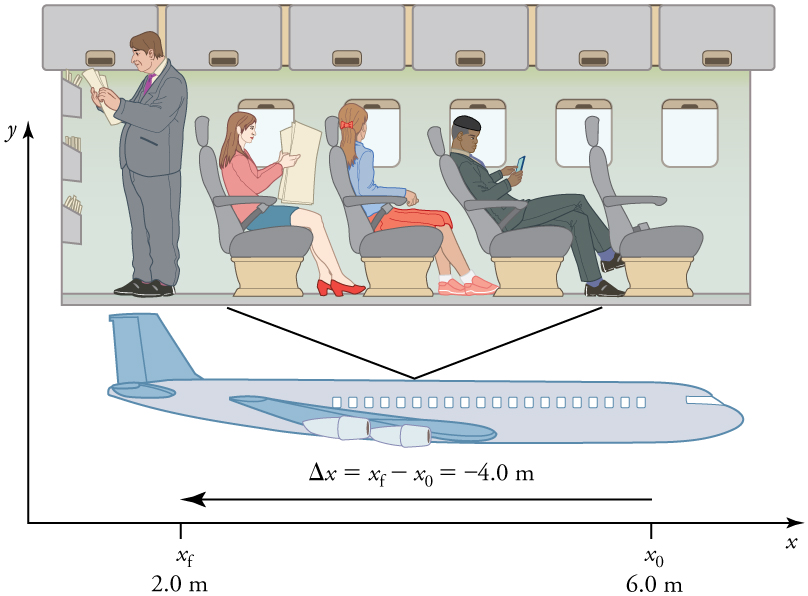
Direction of displacement
Note that displacement has a direction as well as a magnitude. The professor’s displacement is 2.0 m to the right, and the airline passenger’s displacement is 4.0 m toward the rear. In one-dimensional motion, direction can be specified with a plus or minus sign. When you begin a problem, you should select which direction is positive (usually that will be to the right or up, but you are free to select positive as being any direction). The professor’s initial position is [latex]x_i = 1.5m[/latex] and her final position is [latex]x_f = 3.5m[/latex]. Thus her displacement is: [latex]\Delta x = x_f - x_i = 3.5m - 1.5m = +2.0m[/latex].
In this reference frame, motion to the right is positive, whereas motion to the left is negative. Similarly, the airplane passenger’s initial position is[latex]x_i = 6.0m[/latex] and his final position is [latex]x_f = 2.0m[/latex], so his displacement is: [latex]\Delta x = x_f - x_i = 2.0m - 6.0m = -4.0m[/latex].
His displacement is negative because his motion is toward the rear of the plane, or in the negative [latex]x[/latex] direction in our reference frame.
Total displacement
Objects in motion can also have a series of displacements. For example, if the professor in the example above walked 3.0m to the left (from position 3.5m to 0.5m), then this would represent a second displacement of -3.0m ([latex]\Delta x = x_f - x_i = 0.5m - 3.5m = -3.0m[/latex]). We define total displacement as the sum of the individual displacements.
Total displacement is calculated as:
[latex]\Delta x_{total} = \sum \Delta x_i = x_1 + x_2 + x_3 ..... + x_i[/latex]
where
[latex]\Delta x_i[/latex] are the individual displacements ([latex]x_1, x_2, x_3[/latex]...and so on)
Distance
Although displacement is described in terms of direction and magnitude, distance is not. Distance is defined as the magnitude or size of displacement between two positions. Note that the distance between two positions is not the same as the distance traveled between them. Distance traveled is the total length of the path traveled between two positions. Distance and distance travelled have no direction and, thus, no sign. For example, the distance the professor walks is 2.0 m. The distance the airplane passenger walks is 4.0 m.
Misconception Alert: Distance Travelled vs. Magnitude of Displacement
It is important to note that the distance traveled, however, can be greater than the magnitude of the displacement (by magnitude, we mean just the size of the displacement without regard to its direction; that is, just a number with a unit). For example, the professor could pace back and forth many times, perhaps walking a distance of 150 m during a lecture, yet still end up only 2.0 m to the right of her starting point. In this case her displacement would be +2.0 m, the magnitude of her displacement would be 2.0 m, but the distance she traveled would be 150 m. In biomechanics we may deal with displacement, magnitude of displacement and distance travelled depending on the situation. One way to think about this is to assume you marked the start of the motion and the end of the motion. The displacement is simply the difference in the position of the two marks and is independent of the path taken in traveling between the two marks. The distance traveled, however, is the total length of the path taken between the two marks.
Check your Understanding
A cyclist rides 3 km west and then turns around and rides 2 km east.
(a) What are their individual displacements?
(b) What is their total displacements?
(c) What distance do they ride?
(d) What is the magnitude of their total displacement?
Solution
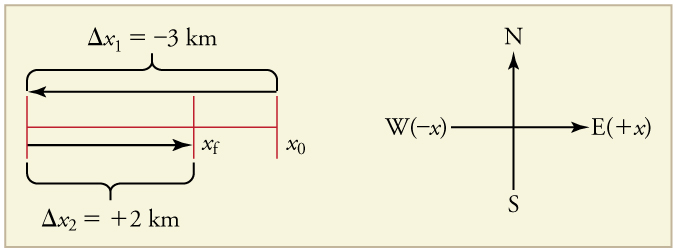
(a) The rider’s first displacement is:
[latex]\Delta x = x_f - x_i = 0 - (-3.0)\text{km} = -3.0\text{km}[/latex].
Similarly, their second displacement is:
[latex]\Delta x = x_f - x_i = -1.0\text{km} - (-3.0)\text{km} = +2.0\text{km}[/latex].
(we define their starting position to be zero, and west to be negative and east to be positive).
(b) Their total displacement is:
[latex]\Delta x_{total} = x_1 + x_2 = -3.0\text{km} + 2.0\text{km} = -1.0\text{km}[/latex]
(c) The distance traveled is 3km + 2km = 5km.
(d) The magnitude of their total displacement is 1.0km.

