Chapter 6: Linear Momentum and Collisions
6.4 Elastic Collisions in One Dimension
Authors: Paul Peter Urone, Roger Hinrichs
Adapted by: Rob Pryce, Alix Blacklin
Learning Objectives
By the end of this section, you will be able to:
- Describe an elastic collision of two objects in one dimension.
- Define internal kinetic energy.
- Derive an expression for conservation of internal kinetic energy in a one dimensional collision.
- Determine the final velocities in an elastic collision given masses and initial velocities.
Let us consider various types of two-object collisions. These collisions are the easiest to analyze, and they illustrate many of the physical principles involved in collisions. The conservation of momentum principle is very useful here, and it can be used whenever the net external force on a system is zero.
We start with the elastic collision of two objects moving along the same line—a one-dimensional problem. An elastic collision is one that also conserves internal kinetic energy. Internal kinetic energy is the sum of the kinetic energies of the objects in the system. The figure below illustrates an elastic collision in which internal kinetic energy and momentum are conserved.
Truly elastic collisions can only be achieved with subatomic particles, such as electrons striking nuclei. Macroscopic collisions can be very nearly, but not quite, elastic—some kinetic energy is always converted into other forms of energy such as heat transfer due to friction and sound. One macroscopic collision that is nearly elastic is that of two steel blocks on ice. Another nearly elastic collision is that between two carts with spring bumpers on an air track. Icy surfaces and air tracks are nearly frictionless, more readily allowing nearly elastic collisions on them.
Elastic Collision
An elastic collision is one that conserves internal kinetic energy. (note that momentum is also conserved)
Internal Kinetic Energy
Internal kinetic energy is the sum of the kinetic energies of the objects in the system.
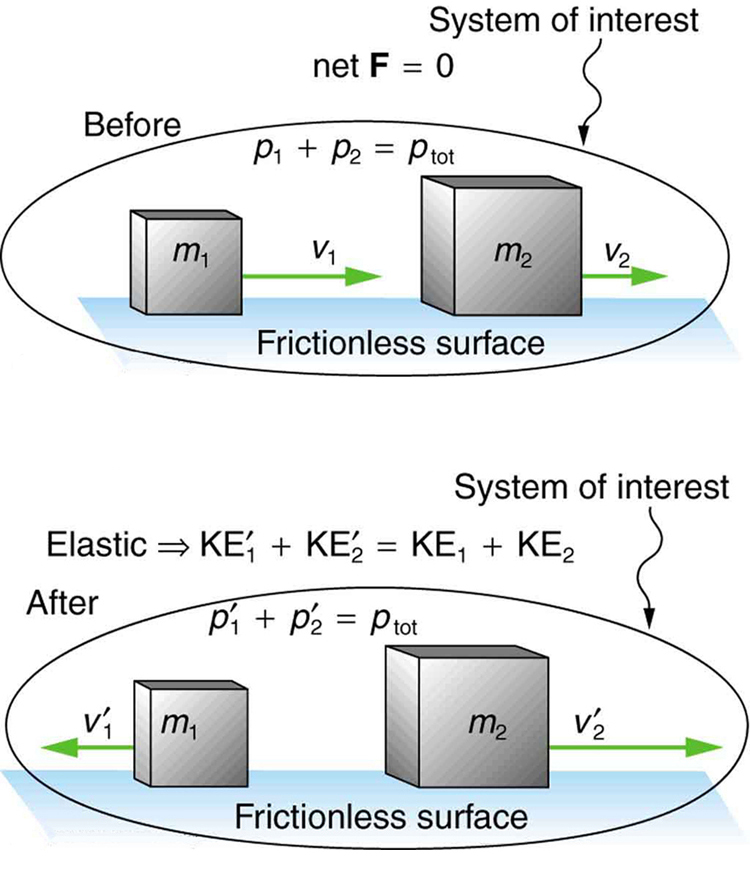
Now, to solve problems involving one-dimensional elastic collisions between two objects we can use the equations for conservation of momentum and conservation of internal kinetic energy. First, the equation for conservation of momentum for two objects in a one-dimensional collision is
where the primes (') indicate values after the collision. By definition, an elastic collision conserves internal kinetic energy, and so the sum of kinetic energies before the collision equals the sum after the collision. Thus,
expresses the equation for conservation of internal kinetic energy in a one-dimensional collision.
Alternatively, these equations can also be expressed relative to the post-collision velocities of each object. In these cases:
[latex]v\prime_1 = \frac{2m_2v_2 + \left(m_1 - m_2\right)v_1}{m_1 + m_2}[/latex], and
[latex]v\prime_2 = \frac{2m_1v_1 + \left(m_2 - m_1\right)v_2}{m_1 + m_2}[/latex]
Example: Calculating Velocities Following an Elastic Collision
Calculate the velocities of two objects following an elastic collision, given that
Strategy and Concept
First, visualize what the initial conditions mean—a small object strikes a larger object that is initially at rest. This situation is slightly simpler than the situation shown in the figure above where both objects are initially moving. To find the final velocities, we can use the two equations above.
Solution
The post-collision velocity of object one can be calculated using: [latex]v\prime_1 = \frac{2m_2v_2 + \left(m_1 - m_2\right)v_1}{m_1 + m_2}[/latex], where:
[latex]v\prime_1 = \frac{2*3.5 kg*0 + \left(0.5 kg - 3.5 kg\right)*4 m/s}{0.5 kg + 3.5 kg}[/latex], and
[latex]v\prime_1 = -3.0 m/s[/latex]
The negative velocity indicates that the object is travelling in the opposite direction as the start.
To determine the velocity of object two we can either use the second equation above [latex]v\prime_2 = \frac{2m_1v_1 + \left(m_2 - m_1\right)v_2}{m_1 + m_2}[/latex], or we can use the more simple equation for conservation of momentum:
[latex]{m}_{1}{v}_{1}+{m}_{2}{v}_{2}={m}_{1}{v\prime }_{1}+{m}_{2}{v\prime }_{2}\phantom{\rule{0.25em}{0ex}}\phantom{\rule{0.25em}{0ex}}\phantom{\rule{0.25em}{0ex}}[/latex].
Using the calculated value for the post-collision velocity of object 1 from above, we can see this equation contains only one unknown and can be solved for [latex]v\prime_2[/latex]:
[latex]v\prime_2 = \frac {{m}_{1}{v}_{1}+{m}_{2}{v}_{2} - m_1v\prime_1}{m_2}[/latex]
[latex]v\prime_2 = \frac {0.5 kg * 4.0 m/s + 3.5kg * 0 - 0.5kg *-3.0 m/s}{3.5} = 1.0 m/s[/latex]
This velocity indicates that object 2 is moving in the same direction as object 1 was before the collision, but at a slower speed. (note: we can also check our answers by confirming that the pre- and post-collision momentum is conserved)
Discussion
The result of this example is intuitively reasonable. A small object strikes a larger one at rest and bounces backward. The larger one is knocked forward, but with a low speed. (This is like a compact car bouncing backward off a full-size SUV that is initially at rest.) As a check, try calculating the internal kinetic energy before and after the collision. You will see that the internal kinetic energy is unchanged at 4.00 J. Also check the total momentum before and after the collision; you will find it, too, is unchanged.
The equations for conservation of momentum and internal kinetic energy as written above can be used to describe any one-dimensional elastic collision of two objects. These equations can be extended to more objects if needed.
Alternative Solution
Alternatively, this problem can also be solved using the basic formulas for conservation of momentum and kinetic energy above. For this problem, note that [latex]{v}_{2}=0[/latex] and use conservation of momentum. Thus,
or
Using conservation of internal kinetic energy and that [latex]{v}_{2}=0[/latex],
Solving the first equation (momentum equation) for [latex]{v\prime }_{2}[/latex], we obtain
Substituting this expression into the second equation (internal kinetic energy equation) eliminates the variable [latex]{v\prime }_{2}[/latex], leaving only [latex]{v\prime }_{1}[/latex] as an unknown (the algebra is left as an exercise for the reader). There are two solutions to any quadratic equation; in this example, they are
and
As noted when quadratic equations were encountered in earlier chapters, both solutions may or may not be meaningful. In this case, the first solution is the same as the initial condition. The first solution thus represents the situation before the collision and is discarded. The second solution [latex]\left({v\prime }_{1}=-3\text{.}\text{00 m/s}\right)[/latex] is negative, meaning that the first object bounces backward. When this negative value of [latex]{v\prime }_{1}[/latex] is used to find the velocity of the second object after the collision, we get
or
Investigate collisions on an air hockey table using this PhET simulation. Set up your own experiments: vary the number of discs, masses and initial conditions. Is momentum conserved? Is kinetic energy conserved? Vary the elasticity and see what happens.

