59 Phase Transitions

Learning Objectives

By the end of this section, you will be able to:

  • Define phase transitions and phase transition temperatures
  • Explain the relation between phase transition temperatures and intermolecular attractive forces
  • Describe the processes represented by typical heating and cooling curves, and compute heat flows and enthalpy changes accompanying these processes

We witness and utilize changes of physical state, or phase transitions, in a great number of ways. As one example of global significance, consider the evaporation, condensation, freezing, and melting of water. These changes of state are essential aspects of our earth’s water cycle as well as many other natural phenomena and technological processes of central importance to our lives. In this module, the essential aspects of phase transitions are explored.

Vaporization and Condensation

When a liquid vaporizes in a closed container, gas molecules cannot escape. As these gas phase molecules move randomly about, they will occasionally collide with the surface of the condensed phase, and in some cases, these collisions will result in the molecules re-entering the condensed phase. The change from the gas phase to the liquid is called condensation. When the rate of condensation becomes equal to the rate of vaporization, neither the amount of the liquid nor the amount of the vapor in the container changes. The vapor in the container is then said to be in equilibrium with the liquid. Keep in mind that this is not a static situation, as molecules are continually exchanged between the condensed and gaseous phases. Such is an example of a dynamic equilibrium, the status of a system in which reciprocal processes (for example, vaporization and condensation) occur at equal rates. The pressure exerted by the vapor in equilibrium with a liquid in a closed container at a given temperature is called the liquid’s vapor pressure (or equilibrium vapor pressure). The area of the surface of the liquid in contact with a vapor and the size of the vessel have no effect on the vapor pressure, although they do affect the time required for the equilibrium to be reached. We can measure the vapor pressure of a liquid by placing a sample in a closed container, like that illustrated in (Figure), and using a manometer to measure the increase in pressure that is due to the vapor in equilibrium with the condensed phase.

In a closed container, dynamic equilibrium is reached when (a) the rate of molecules escaping from the liquid to become the gas (b) increases and eventually (c) equals the rate of gas molecules entering the liquid. When this equilibrium is reached, the vapor pressure of the gas is constant, although the vaporization and condensation processes continue.

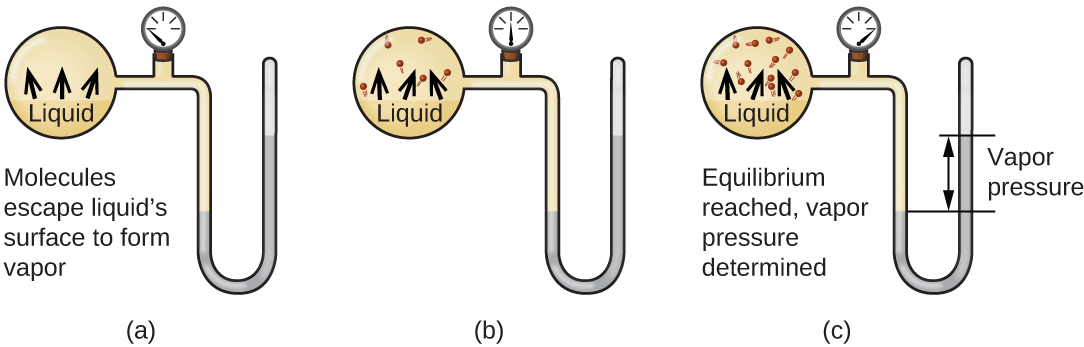
Three images are shown and labeled “a,” “b,” and “c.” Each image shows a round bulb connected on the right to a tube that is horizontal, then is bent vertically, curves, and then is vertical again to make a u-shape. A valve is located in the horizontal portion of the tube. Image a depicts a liquid in the bulb, labeled, “Liquid,” and upward-facing arrows leading away from the surface of the liquid. The phrase, “Molecules escape surface and form vapor” is written below the bulb, and a gray liquid in the u-shaped portion of the tube is shown at equal heights on the right and left sides. Image b depicts a liquid in the bulb, labeled, “Liquid,” and upward-facing arrows leading away from the surface of the liquid to molecules drawn in the upper portion of the bulb. A gray liquid in the u-shaped portion of the tube is shown slightly higher on the right side than on the left side. Image c depicts a liquid in the bulb, labeled, “Liquid,” and upward-facing arrows leading away from the surface of the liquid to molecules drawn in the upper portion of the bulb. There are more molecules present in c than in b. The phrase “Equilibrium reached, vapor pressure determined,” is written below the bulb and a gray liquid in the u-shaped portion of the tube is shown higher on the right side. A horizontal line is drawn level with each of these liquid levels and the distance between the lines is labeled with a double-headed arrow. This section is labeled with the phrase, “Vapor pressure.”

The chemical identities of the molecules in a liquid determine the types (and strengths) of intermolecular attractions possible; consequently, different substances will exhibit different equilibrium vapor pressures. Relatively strong intermolecular attractive forces will serve to impede vaporization as well as favoring “recapture” of gas-phase molecules when they collide with the liquid surface, resulting in a relatively low vapor pressure. Weak intermolecular attractions present less of a barrier to vaporization, and a reduced likelihood of gas recapture, yielding relatively high vapor pressures. The following example illustrates this dependence of vapor pressure on intermolecular attractive forces.

Explaining Vapor Pressure in Terms of IMFs

Given the shown structural formulas for these four compounds, explain their relative vapor pressures in terms of types and extents of IMFs:

Four Lewis structures are shown. The first structure, labeled “ethanol,” shows a carbon bonded to three hydrogen atoms that is single bonded to a second carbon that is bonded to two hydrogen atoms and a hydroxyl group. The second structure, labeled “ethylene glycol, shows two carbon atoms, single bonded to one another, single bonded each to two hydrogen atoms, and each single bonded to a hydroxyl group. The third image, labeled “diethyl ether,” shows an oxygen atom single bonded on both sides to a carbon that is bonded to two hydrogens, and a second carbon, that is itself bonded to three hydrogen atoms. The fourth image, labeled “water,” shows an oxygen atom that is single bonded on both sides to hydrogen atoms.

Solution

Diethyl ether has a very small dipole and most of its intermolecular attractions are London forces. Although this molecule is the largest of the four under consideration, its IMFs are the weakest and, as a result, its molecules most readily escape from the liquid. It also has the highest vapor pressure. Due to its smaller size, ethanol exhibits weaker dispersion forces than diethyl ether. However, ethanol is capable of hydrogen bonding and, therefore, exhibits stronger overall IMFs, which means that fewer molecules escape from the liquid at any given temperature, and so ethanol has a lower vapor pressure than diethyl ether. Water is much smaller than either of the previous substances and exhibits weaker dispersion forces, but its extensive hydrogen bonding provides stronger intermolecular attractions, fewer molecules escaping the liquid, and a lower vapor pressure than for either diethyl ether or ethanol. Ethylene glycol has two −OH groups, so, like water, it exhibits extensive hydrogen bonding. It is much larger than water and thus experiences larger London forces. Its overall IMFs are the largest of these four substances, which means its vaporization rate will be the slowest and, consequently, its vapor pressure the lowest.

Check Your Learning

At 20 °C, the vapor pressures of several alcohols are given in this table. Explain these vapor pressures in terms of types and extents of IMFs for these alcohols:

Compound methanol CH3OH ethanol C2H5OH propanol C3H7OH butanol C4H9OH
Vapor Pressure at 20 °C 11.9 kPa 5.95 kPa 2.67 kPa 0.56 kPa
Answer: All these compounds exhibit hydrogen bonding; these strong IMFs are difficult for the molecules to overcome, so the vapor pressures are relatively low. As the size of molecule increases from methanol to butanol, dispersion forces increase, which means that the vapor pressures decrease as observed:
 Pmethanol > Pethanol > Ppropanol > Pbutanol.

 

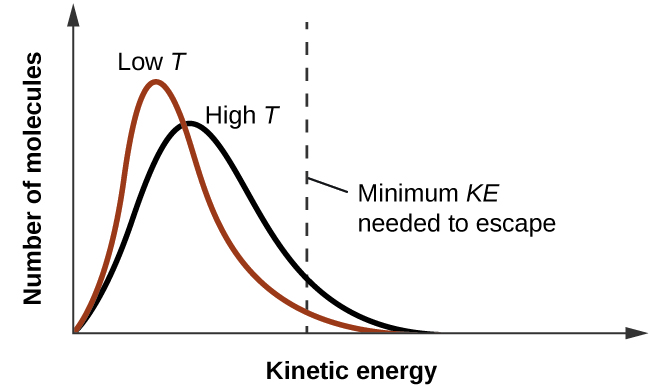
As temperature increases, the vapor pressure of a liquid also increases due to the increased average KE of its molecules. Recall that at any given temperature, the molecules of a substance experience a range of kinetic energies, with a certain fraction of molecules having a sufficient energy to overcome IMF and escape the liquid (vaporize). At a higher temperature, a greater fraction of molecules have enough energy to escape from the liquid, as shown in (Figure). The escape of more molecules per unit of time and the greater average speed of the molecules that escape both contribute to the higher vapor pressure.

Temperature affects the distribution of kinetic energies for the molecules in a liquid. At the higher temperature, more molecules have the necessary kinetic energy, KE, to escape from the liquid into the gas phase.

A graph is shown where the y-axis is labeled “Number of molecules” and the x-axis is labeled “Kinetic Energy.” Two lines are graphed and a vertical dotted line, labeled “Minimum K E needed to escape,” is drawn halfway across the x-axis. The first line move sharply upward and has a high peak near the left side of the x-axis. It drops just as steeply and ends about 60 percent of the way across the x-axis. This line is labeled “Low T.” A second line, labeled “High T,” begins at the same point as the first, but does not go to such a high point, is wider, and ends slightly further to the right on the x-axis.

Boiling Points

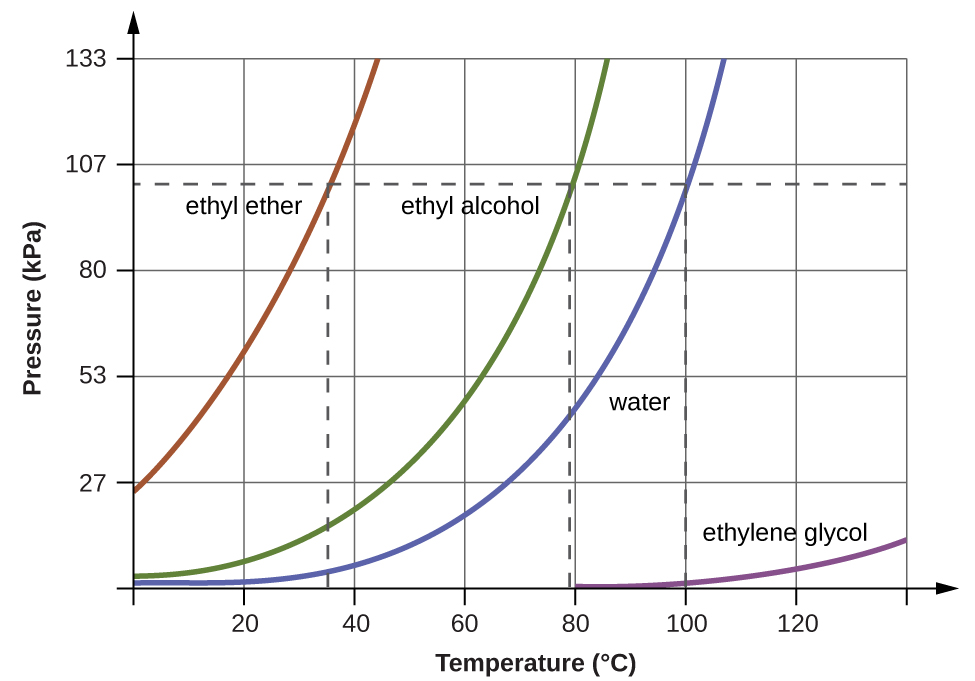
When the vapor pressure increases enough to equal the external atmospheric pressure, the liquid reaches its boiling point. The boiling point of a liquid is the temperature at which its equilibrium vapor pressure is equal to the pressure exerted on the liquid by its gaseous surroundings. For liquids in open containers, this pressure is that due to the earth’s atmosphere. The normal boiling point of a liquid is defined as its boiling point when surrounding pressure is equal to 1 atm (101.3 kPa). (Figure) shows the variation in vapor pressure with temperature for several different substances. Considering the definition of boiling point, these curves may be seen as depicting the dependence of a liquid’s boiling point on surrounding pressure.

The boiling points of liquids are the temperatures at which their equilibrium vapor pressures equal the pressure of the surrounding atmosphere. Normal boiling points are those corresponding to a pressure of 1 atm (101.3 kPa.)

A graph is shown where the x-axis is labeled “Temperature ( degree sign, C )” and has values of 200 to 1000 in increments of 200 and the y-axis is labeled “Pressure ( k P a )” and has values of 20 to 120 in increments of 20. A horizontal dotted line extends across the graph at point 780 on the y-axis while three vertical dotted lines extend from points 35, 78, and 100 to meet the horizontal dotted line. Four lines are graphed. The first line, labeled “ethyl ether,” begins at the point “0 , 200” and extends in a slight curve to point “45, 1000” while the second line, labeled “ethanol”, extends from point “0, 20” to point “88, 1000” in a more extreme curve. The third line, labeled “water,” begins at the point “0, 0” and extends in a curve to point “108, 1000” while the fourth line, labeled “ethylene glycol,” extends from point “80, 0” to point “140, 100” in a very shallow curve.

A Boiling Point at Reduced Pressure

A typical atmospheric pressure in Leadville, Colorado (elevation 10,200 feet) is 68 kPa. Use the graph in (Figure) to determine the boiling point of water at this elevation.

Solution

The graph of the vapor pressure of water versus temperature in (Figure) indicates that the vapor pressure of water is 68 kPa at about 90 °C. Thus, at about 90 °C, the vapor pressure of water will equal the atmospheric pressure in Leadville, and water will boil.

Check Your Learning

The boiling point of ethyl ether was measured to be 10 °C at a base camp on the slopes of Mount Everest. Use (Figure) to determine the approximate atmospheric pressure at the camp.

Answer: Approximately 40 kPa (0.4 atm)

The quantitative relation between a substance’s vapor pressure and its temperature is described by the Clausius-Clapeyron equation:

P=A{e}^{-\text{Δ}{H}_{\text{vap}}\text{/}RT}

where ΔHvap is the enthalpy of vaporization for the liquid, R is the gas constant, and A is a constant whose value depends on the chemical identity of the substance. Temperature T must be in Kelvin in this equation. This equation is often rearranged into logarithmic form to yield the linear equation:

\text{ln}\phantom{\rule{0.2em}{0ex}}P=-\frac{\text{Δ}{H}_{\text{vap}}}{RT}\phantom{\rule{0.2em}{0ex}}+\text{ln}\phantom{\rule{0.2em}{0ex}}A

This linear equation may be expressed in a two-point format that is convenient for use in various computations, as demonstrated in the example exercises that follow. If at temperature T1, the vapor pressure is P1, and at temperature T2, the vapor pressure is P2, the corresponding linear equations are:

\text{ln}\phantom{\rule{0.2em}{0ex}}{P}_{1}=-\frac{\text{Δ}{H}_{\text{vap}}}{R{T}_{1}}\phantom{\rule{0.2em}{0ex}}+\text{ln}\phantom{\rule{0.2em}{0ex}}A\phantom{\rule{5em}{0ex}}\text{and}\phantom{\rule{5em}{0ex}}\text{ln}\phantom{\rule{0.2em}{0ex}}{P}_{2}=-\frac{\text{Δ}{H}_{\text{vap}}}{R{T}_{2}}\phantom{\rule{0.2em}{0ex}}+\text{ln}\phantom{\rule{0.2em}{0ex}}A

Since the constant, A, is the same, these two equations may be rearranged to isolate ln A and then set them equal to one another:

\text{ln}\phantom{\rule{0.2em}{0ex}}{P}_{1}+\phantom{\rule{0.2em}{0ex}}\frac{\text{Δ}{H}_{\text{vap}}}{R{T}_{1}}\phantom{\rule{0.2em}{0ex}}=\text{ln}\phantom{\rule{0.2em}{0ex}}{P}_{2}+\phantom{\rule{0.2em}{0ex}}\frac{\text{Δ}{H}_{\text{vap}}}{R{T}_{2}}

which can be combined into:

\text{ln}\phantom{\rule{0.2em}{0ex}}\left(\frac{{P}_{2}}{{P}_{1}}\right)=\phantom{\rule{0.2em}{0ex}}\frac{\text{Δ}{H}_{\text{vap}}}{R}\phantom{\rule{0.2em}{0ex}}\left(\frac{1}{{T}_{1}}\phantom{\rule{0.2em}{0ex}}-\phantom{\rule{0.2em}{0ex}}\frac{1}{{T}_{2}}\right)

Estimating Enthalpy of Vaporization

Isooctane (2,2,4-trimethylpentane) has an octane rating of 100. It is used as one of the standards for the octane-rating system for gasoline. At 34.0 °C, the vapor pressure of isooctane is 10.0 kPa, and at 98.8 °C, its vapor pressure is 100.0 kPa. Use this information to estimate the enthalpy of vaporization for isooctane.

Solution

The enthalpy of vaporization, ΔHvap, can be determined by using the Clausius-Clapeyron equation:

\text{ln}\phantom{\rule{0.2em}{0ex}}\left(\frac{{P}_{2}}{{P}_{1}}\right)=\phantom{\rule{0.2em}{0ex}}\frac{\text{Δ}{H}_{\text{vap}}}{R}\phantom{\rule{0.2em}{0ex}}\left(\frac{1}{{T}_{1}}\phantom{\rule{0.2em}{0ex}}-\phantom{\rule{0.2em}{0ex}}\frac{1}{{T}_{2}}\right)

Since we have two vapor pressure-temperature values (T1 = 34.0 °C = 307.2 K, P1 = 10.0 kPa and T2 = 98.8 °C = 372.0 K, P2 = 100 kPa), we can substitute them into this equation and solve for ΔHvap. Rearranging the Clausius-Clapeyron equation and solving for ΔHvap yields:

\text{Δ}{H}_{\text{vap}}=\phantom{\rule{0.2em}{0ex}}\frac{R\text{⋅}\text{ln}\phantom{\rule{0.2em}{0ex}}\left(\frac{{P}_{2}}{{P}_{1}}\right)}{\left(\frac{1}{{T}_{1}}\phantom{\rule{0.2em}{0ex}}-\phantom{\rule{0.2em}{0ex}}\frac{1}{{T}_{2}}\right)}\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}\frac{\left(8.3145\phantom{\rule{0.2em}{0ex}}\text{J/mol}\text{⋅}\text{K}\right)\text{⋅}\text{ln}\phantom{\rule{0.2em}{0ex}}\left(\frac{\text{100 kPa}}{\text{10.0 kPa}}\right)}{\left(\frac{1}{307.2\phantom{\rule{0.2em}{0ex}}\text{K}}\phantom{\rule{0.2em}{0ex}}-\phantom{\rule{0.2em}{0ex}}\frac{1}{372.0\phantom{\rule{0.2em}{0ex}}\text{K}}\right)}\phantom{\rule{0.2em}{0ex}}=\text{33,800 J/mol}=\text{33.8 kJ/mol}

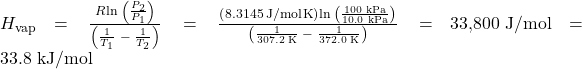
Note that the pressure can be in any units, so long as they agree for both P values, but the temperature must be in kelvin for the Clausius-Clapeyron equation to be valid.

Check Your Learning

At 20.0 °C, the vapor pressure of ethanol is 5.95 kPa, and at 63.5 °C, its vapor pressure is 53.3 kPa. Use this information to estimate the enthalpy of vaporization for ethanol.

Answer: 41,360 J/mol or 41.4 kJ/mol<!– no-selfclose –>

Estimating Temperature (or Vapor Pressure)

For benzene (C6H6), the normal boiling point is 80.1 °C and the enthalpy of vaporization is 30.8 kJ/mol. What is the boiling point of benzene in Denver, where atmospheric pressure = 83.4 kPa?

Solution

If the temperature and vapor pressure are known at one point, along with the enthalpy of vaporization, ΔHvap, then the temperature that corresponds to a different vapor pressure (or the vapor pressure that corresponds to a different temperature) can be determined by using the Clausius-Clapeyron equation:

\text{ln}\phantom{\rule{0.2em}{0ex}}\left(\frac{{P}_{2}}{{P}_{1}}\right)=\phantom{\rule{0.2em}{0ex}}\frac{\text{Δ}{H}_{\text{vap}}}{R}\phantom{\rule{0.2em}{0ex}}\left(\frac{1}{{T}_{1}}\phantom{\rule{0.2em}{0ex}}-\phantom{\rule{0.2em}{0ex}}\frac{1}{{T}_{2}}\right)

Since the normal boiling point is the temperature at which the vapor pressure equals atmospheric pressure at sea level, we know one vapor pressure-temperature value (T1 = 80.1 °C = 353.3 K, P1 = 101.3 kPa, ΔHvap = 30.8 kJ/mol) and want to find the temperature (T2) that corresponds to vapor pressure P2 = 83.4 kPa. We can substitute these values into the Clausius-Clapeyron equation and then solve for T2. Rearranging the Clausius-Clapeyron equation and solving for T2 yields:

{T}_{2}={\left(\frac{-R\text{⋅}\text{ln}\phantom{\rule{0.2em}{0ex}}\left(\frac{{P}_{2}}{{P}_{1}}\right)}{\text{Δ}{H}_{\text{vap}}}\phantom{\rule{0.2em}{0ex}}+\phantom{\rule{0.2em}{0ex}}\frac{1}{{T}_{1}}\right)}^{-1}={\left(\frac{-\left(8.3145\phantom{\rule{0.2em}{0ex}}\text{J/mol}\text{⋅}\text{K}\right)\text{⋅}\text{ln}\phantom{\rule{0.2em}{0ex}}\left(\frac{83.4\phantom{\rule{0.2em}{0ex}}\text{kPa}}{101.3\phantom{\rule{0.2em}{0ex}}\text{kPa}}\right)}{\text{30,800 J/mol}}\phantom{\rule{0.2em}{0ex}}+\phantom{\rule{0.2em}{0ex}}\frac{1}{353.3\phantom{\rule{0.2em}{0ex}}\text{K}}\right)}^{-1}=\text{346.9 K or}\phantom{\rule{0.2em}{0ex}}{73.8}^{\circ }\text{C}

 

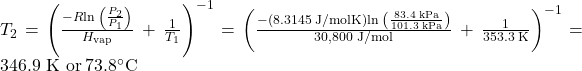
Check Your Learning

For acetone (CH3)2CO, the normal boiling point is 56.5 °C and the enthalpy of vaporization is 31.3 kJ/mol. What is the vapor pressure of acetone at 25.0 °C?

Answer: 30.1 kPa

 

Enthalpy of Vaporization

Vaporization is an endothermic process. The cooling effect can be evident when you leave a swimming pool or a shower. When the water on your skin evaporates, it removes heat from your skin and causes you to feel cold. The energy change associated with the vaporization process is the enthalpy of vaporization, ΔHvap. For example, the vaporization of water at standard temperature is represented by:

{\text{H}}_{2}\text{O(}l\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{2}\text{O(}g\right)\phantom{\rule{5em}{0ex}}\text{Δ}{H}_{\text{vap}}=\text{44.01 kJ/mol}

As described in the chapter on thermochemistry, the reverse of an endothermic process is exothermic. And so, the condensation of a gas releases heat:

{\text{H}}_{2}\text{O}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{2}\text{O(}l\right)\phantom{\rule{5em}{0ex}}\text{Δ}{H}_{\text{con}}=\text{−Δ}{H}_{\text{vap}}=-44.01\phantom{\rule{0.2em}{0ex}}\text{kJ/mol}

Using Enthalpy of Vaporization

One way our body is cooled is by evaporation of the water in sweat ((Figure)). In very hot climates, we can lose as much as 1.5 L of sweat per day. Although sweat is not pure water, we can get an approximate value of the amount of heat removed by evaporation by assuming that it is. How much heat is required to evaporate 1.5 L of water (1.5 kg) at T = 37 °C (normal body temperature); ΔHvap = 43.46 kJ/mol at 37 °C.

Evaporation of sweat helps cool the body. (credit: “Kullez”/Flickr)

A person’s shoulder and neck are shown and their skin is covered in beads of liquid.

Solution

We start with the known volume of sweat (approximated as just water) and use the given information to convert to the amount of heat needed:

1.5\phantom{\rule{0.2em}{0ex}}\overline{)\text{L}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\frac{1000\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}}{1\overline{)\text{L}}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\frac{1\phantom{\rule{0.2em}{0ex}}\overline{)\text{mol}}}{18\phantom{\rule{0.2em}{0ex}}\overline{)\text{g}}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\frac{43.46\phantom{\rule{0.2em}{0ex}}\text{kJ}}{1\phantom{\rule{0.2em}{0ex}}\overline{)\text{mol}}}\phantom{\rule{0.2em}{0ex}}=3.6\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{3}\phantom{\rule{0.2em}{0ex}}\text{kJ}

Thus, 3600 kJ of heat are removed by the evaporation of 1.5 L of water.

Check Your Learning

How much heat is required to evaporate 100.0 g of liquid ammonia, NH3, at its boiling point if its enthalpy of vaporization is 4.8 kJ/mol?

Answer: 28 kJ

Melting and Freezing

When we heat a crystalline solid, we increase the average energy of its atoms, molecules, or ions and the solid gets hotter. At some point, the added energy becomes large enough to partially overcome the forces holding the molecules or ions of the solid in their fixed positions, and the solid begins the process of transitioning to the liquid state, or melting. At this point, the temperature of the solid stops rising, despite the continual input of heat, and it remains constant until all of the solid is melted. Only after all of the solid has melted will continued heating increase the temperature of the liquid ((Figure)).

(a) This beaker of ice has a temperature of −12.0 °C. (b) After 10 minutes the ice has absorbed enough heat from the air to warm to 0 °C. A small amount has melted. (c) Thirty minutes later, the ice has absorbed more heat, but its temperature is still 0 °C. The ice melts without changing its temperature. (d) Only after all the ice has melted does the heat absorbed cause the temperature to increase to 22.2 °C. (credit: modification of work by Mark Ott)

This figure shows four photos each labeled, “a,” “b,” “c,” and, “d.” Each photo shows a beaker with ice and a digital thermometer. The first photo shows ice cubes in the beaker, and the thermometer reads negative 12.0 degrees C. The second photo shows slightly melted ice, and the thermometer reads 0.0 degrees C. The third photo shows more water than ice in the beaker. The thermometer reads 0.0 degrees C. The fourth photo shows the ice completely melted, and the thermometer reads 22.2 degrees C.

If we stop heating during melting and place the mixture of solid and liquid in a perfectly insulated container so no heat can enter or escape, the solid and liquid phases remain in equilibrium. This is almost the situation with a mixture of ice and water in a very good thermos bottle; almost no heat gets in or out, and the mixture of solid ice and liquid water remains for hours. In a mixture of solid and liquid at equilibrium, the reciprocal processes of melting and freezing occur at equal rates, and the quantities of solid and liquid therefore remain constant. The temperature at which the solid and liquid phases of a given substance are in equilibrium is called the melting point of the solid or the freezing point of the liquid. Use of one term or the other is normally dictated by the direction of the phase transition being considered, for example, solid to liquid (melting) or liquid to solid (freezing).

The enthalpy of fusion and the melting point of a crystalline solid depend on the strength of the attractive forces between the units present in the crystal. Molecules with weak attractive forces form crystals with low melting points. Crystals consisting of particles with stronger attractive forces melt at higher temperatures.

The amount of heat required to change one mole of a substance from the solid state to the liquid state is the enthalpy of fusion, ΔHfus of the substance. The enthalpy of fusion of ice is 6.0 kJ/mol at 0 °C. Fusion (melting) is an endothermic process:

{\text{H}}_{2}\text{O}\left(s\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{2}\text{O(}l\right)\phantom{\rule{5em}{0ex}}\text{Δ}{H}_{\text{fus}}=\text{6.01 kJ/mol}

The reciprocal process, freezing, is an exothermic process whose enthalpy change is −6.0 kJ/mol at 0 °C:

{\text{H}}_{2}\text{O}\left(l\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{H}}_{2}\text{O(}s\right)\phantom{\rule{5em}{0ex}}\text{Δ}{H}_{\text{frz}}=\text{−Δ}{H}_{\text{fus}}=-6.01\phantom{\rule{0.2em}{0ex}}\text{kJ/mol}

Sublimation and Deposition

Some solids can transition directly into the gaseous state, bypassing the liquid state, via a process known as sublimation. At room temperature and standard pressure, a piece of dry ice (solid CO2) sublimes, appearing to gradually disappear without ever forming any liquid. Snow and ice sublime at temperatures below the melting point of water, a slow process that may be accelerated by winds and the reduced atmospheric pressures at high altitudes. When solid iodine is warmed, the solid sublimes and a vivid purple vapor forms ((Figure)). The reverse of sublimation is called deposition, a process in which gaseous substances condense directly into the solid state, bypassing the liquid state. The formation of frost is an example of deposition.

Sublimation of solid iodine in the bottom of the tube produces a purple gas that subsequently deposits as solid iodine on the colder part of the tube above. (credit: modification of work by Mark Ott)

This figure shows a test tube. In the bottom is a dark substance which breaks up into a purple gas at the top.

Like vaporization, the process of sublimation requires an input of energy to overcome intermolecular attractions. The enthalpy of sublimation, ΔHsub, is the energy required to convert one mole of a substance from the solid to the gaseous state. For example, the sublimation of carbon dioxide is represented by:

{\text{CO}}_{2}\left(s\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CO}}_{2}\left(g\right)\phantom{\rule{5em}{0ex}}\text{Δ}{H}_{\text{sub}}=\text{26.1 kJ/mol}

Likewise, the enthalpy change for the reverse process of deposition is equal in magnitude but opposite in sign to that for sublimation:

{\text{CO}}_{2}\left(g\right)\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}{\text{CO}}_{2}\left(s\right)\phantom{\rule{5em}{0ex}}\text{Δ}{H}_{\text{dep}}=\text{−Δ}{H}_{\text{sub}}=-26.1\phantom{\rule{0.2em}{0ex}}\text{kJ/mol}

Consider the extent to which intermolecular attractions must be overcome to achieve a given phase transition. Converting a solid into a liquid requires that these attractions be only partially overcome; transition to the gaseous state requires that they be completely overcome. As a result, the enthalpy of fusion for a substance is less than its enthalpy of vaporization. This same logic can be used to derive an approximate relation between the enthalpies of all phase changes for a given substance. Though not an entirely accurate description, sublimation may be conveniently modeled as a sequential two-step process of melting followed by vaporization in order to apply Hess’s Law. Viewed in this manner, the enthalpy of sublimation for a substance may be estimated as the sum of its enthalpies of fusion and vaporization, as illustrated in (Figure). For example:

\begin{array}{l}\text{solid}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{liquid}\phantom{\rule{5em}{0ex}}\text{Δ}{H}_{\text{fus}}\\ \underset{¯}{\text{liquid}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{gas}\phantom{\rule{5em}{0ex}}\text{Δ}{H}_{\text{vap}}}\\ \text{solid}\phantom{\rule{0.2em}{0ex}}⟶\phantom{\rule{0.2em}{0ex}}\text{gas}\phantom{\rule{5em}{0ex}}\text{Δ}{H}_{\text{sub}}=\text{Δ}{H}_{\text{fus}}+\text{Δ}{H}_{\text{vap}}\end{array}
For a given substance, the sum of its enthalpy of fusion and enthalpy of vaporization is approximately equal to its enthalpy of sublimation.

A diagram is shown with a vertical line drawn on the left side and labeled “Energy” and three horizontal lines drawn near the bottom, lower third and top of the diagram. These three lines are labeled, from bottom to top, “Solid,” “Liquid” and “Gas.” Near the middle of the diagram, a vertical, upward-facing arrow is drawn from the solid line to the gas line and labeled “Sublimation, delta sign, H, subscript sub.” To the right of this arrow is a second vertical, upward-facing arrow that is drawn from the solid line to the liquid line and labeled “Fusion, delta sign, H, subscript fus.” Above the second arrow is a third arrow drawn from the liquid line to the gas line and labeled, “Vaporization, delta sign, H, subscript vap.”

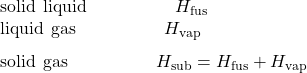
Heating and Cooling Curves

In the chapter on thermochemistry, the relation between the amount of heat absorbed or released by a substance, q, and its accompanying temperature change, ΔT, was introduced:

q=mc\text{Δ}T

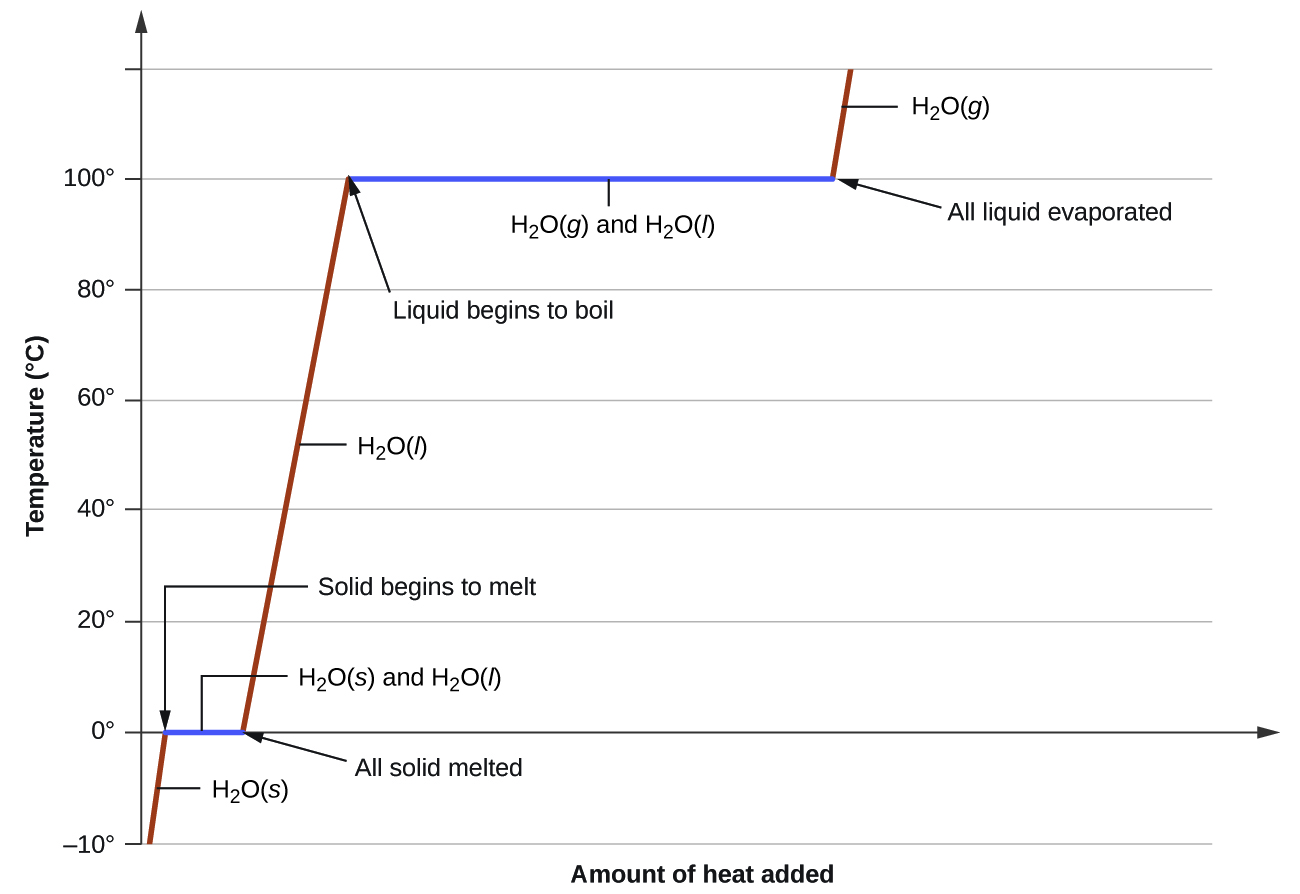
where m is the mass of the substance and c is its specific heat. The relation applies to matter being heated or cooled, but not undergoing a change in state. When a substance being heated or cooled reaches a temperature corresponding to one of its phase transitions, further gain or loss of heat is a result of diminishing or enhancing intermolecular attractions, instead of increasing or decreasing molecular kinetic energies. While a substance is undergoing a change in state, its temperature remains constant. (Figure) shows a typical heating curve.

Consider the example of heating a pot of water to boiling. A stove burner will supply heat at a roughly constant rate; initially, this heat serves to increase the water’s temperature. When the water reaches its boiling point, the temperature remains constant despite the continued input of heat from the stove burner. This same temperature is maintained by the water as long as it is boiling. If the burner setting is increased to provide heat at a greater rate, the water temperature does not rise, but instead the boiling becomes more vigorous (rapid). This behavior is observed for other phase transitions as well: For example, temperature remains constant while the change of state is in progress.

A typical heating curve for a substance depicts changes in temperature that result as the substance absorbs increasing amounts of heat. Plateaus in the curve (regions of constant temperature) are exhibited when the substance undergoes phase transitions.

A graph is shown where the x-axis is labeled “Amount of heat added” and the y-axis is labeled “Temperature ( degree sign C )” and has values of negative 10 to 100 in increments of 20. A right-facing horizontal arrow extends from point “0, 0” to the right side of the graph. A line graph begins at the lower left of the graph and moves to point “0” on the y-axis. This segment of the line is labeled “H, subscript 2, O ( s ).” The line then flattens and travels horizontally for a small distance. This segment is labeled “Solid begins to melt” on its left side and “All solid melted” on its right side. The line then goes steeply upward in a linear fashion until it hits point “100” on the y-axis. This segment of the line is labeled “H, subscript 2, O,( l ).” The line then flattens and travels horizontally for a moderate distance. This segment is labeled “Liquid begins to boil” on its left side and “All liquid evaporated” on its right side. The line then rises to a point above “100” on the y-axis. This segment of the line is labeled “H, subscript 2, O ( g ).”

Total Heat Needed to Change Temperature and Phase for a Substance

How much heat is required to convert 135 g of ice at −15 °C into water vapor at 120 °C?

Solution

The transition described involves the following steps:

  1. Heat ice from −15 °C to 0 °C
  2. Melt ice
  3. Heat water from 0 °C to 100 °C
  4. Boil water
  5. Heat steam from 100 °C to 120 °C

The heat needed to change the temperature of a given substance (with no change in phase) is: q = m × c × ΔT (see previous chapter on thermochemistry). The heat needed to induce a given change in phase is given by q = n × ΔH.

Using these equations with the appropriate values for specific heat of ice, water, and steam, and enthalpies of fusion and vaporization, we have:

{q}_{\text{total}}={\left(m\text{⋅}c\text{⋅}\text{Δ}T\right)}_{\text{ice}}+n\text{⋅}\text{Δ}{H}_{\text{fus}}+{\left(m\text{⋅}c\text{⋅}\text{Δ}T\right)}_{\text{water}}+n\text{⋅}\text{Δ}{H}_{\text{vap}}+{\left(m\text{⋅}c\text{⋅}\text{Δ}T\right)}_{\text{steam}}
\begin{array}{}\\ \\ =\left(\text{135 g}\text{⋅}\text{2.09 J/g}\text{⋅}\text{°}\text{C}\text{⋅}15\text{°}\text{C}\right)+\left(135\text{⋅}\frac{\text{1 mol}}{18.02\phantom{\rule{0.2em}{0ex}}\text{g}}\text{⋅}\text{6.01 kJ/mol}\right)\phantom{\rule{0.2em}{0ex}}\\ +\left(\text{135 g}\text{⋅}\text{4.18 J/g}\text{⋅}\text{°}\text{C}\text{⋅}100\text{°}\text{C}\right)+\left(\text{135 g}\text{⋅}\frac{\text{1 mol}}{18.02\phantom{\rule{0.2em}{0ex}}\text{g}}\text{⋅}\text{40.67 kJ/mol}\right)\\ +\left(\text{135 g}\text{⋅}\text{1.84 J/g}\text{⋅}\text{°}\text{C}\text{⋅}20\text{°}\text{C}\right)\\ =\text{4230 J}+\text{45.0 kJ}+\text{56,500 J}+\text{305 kJ}+\text{4970 J}\end{array}

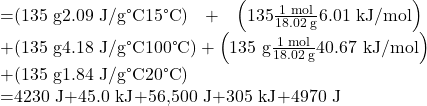
Converting the quantities in J to kJ permits them to be summed, yielding the total heat required:

=4.23\phantom{\rule{0.2em}{0ex}}\text{kJ}+\text{45.0 kJ}+\text{56.5 kJ}+\text{305 kJ}+\text{4.97 kJ}=\text{416 kJ}

 

Check Your Learning

What is the total amount of heat released when 94.0 g water at 80.0 °C cools to form ice at −30.0 °C?

Answer: 68.7 kJ

Key Concepts and Summary

Phase transitions are processes that convert matter from one physical state into another. There are six phase transitions between the three phases of matter. Melting, vaporization, and sublimation are all endothermic processes, requiring an input of heat to overcome intermolecular attractions. The reciprocal transitions of freezing, condensation, and deposition are all exothermic processes, involving heat as intermolecular attractive forces are established or strengthened. The temperatures at which phase transitions occur are determined by the relative strengths of intermolecular attractions and are, therefore, dependent on the chemical identity of the substance.

Key Equations

  • P=A{e}^{-\text{Δ}{H}_{\text{vap}}\text{/}RT}
  • \text{ln}\phantom{\rule{0.2em}{0ex}}P=-\frac{\text{Δ}{H}_{\text{vap}}}{RT}\phantom{\rule{0.2em}{0ex}}+\text{ln}\phantom{\rule{0.2em}{0ex}}A
  • \text{ln}\phantom{\rule{0.2em}{0ex}}\left(\frac{{P}_{2}}{{P}_{1}}\right)\phantom{\rule{0.2em}{0ex}}=\phantom{\rule{0.2em}{0ex}}\frac{\text{Δ}{H}_{\text{vap}}}{R}\phantom{\rule{0.2em}{0ex}}\left(\frac{1}{{T}_{1}}\phantom{\rule{0.2em}{0ex}}-\phantom{\rule{0.2em}{0ex}}\frac{1}{{T}_{2}}\right)

Chemistry End of Chapter Exercises

Instructions 

Complete the following exercises by providing answers to each question. There are a total of 24 questions in this section. Please be aware that certain questions may contain subsections.

 

1. Heat is added to boiling water. Explain why the temperature of the boiling water does not change. What does change?

 

2. Heat is added to ice at 0 °C. Explain why the temperature of the ice does not change. What does change?

Answer(s): The heat is absorbed by the ice, providing the energy required to partially overcome intermolecular attractive forces in the solid and causing a phase transition to liquid water. The solution remains at 0 °C until all the ice is melted. Only the amount of water existing as ice changes until the ice disappears. Then the temperature of the water can rise.

 

3. What feature characterizes the dynamic equilibrium between a liquid and its vapor in a closed container?

 

4. Identify two common observations indicating some liquids have sufficient vapor pressures to noticeably evaporate?

Answer(s): We can see the amount of liquid in an open container decrease and we can smell the vapor of some liquids.

 

5. Identify two common observations indicating some solids, such as dry ice and mothballs, have vapor pressures sufficient to sublime?

 

6. What is the relationship between the intermolecular forces in a liquid and its vapor pressure?

Answer(s):The vapor pressure of a liquid decreases as the strength of its intermolecular forces increases.

 

7. What is the relationship between the intermolecular forces in a solid and its melting temperature?

 

8. Why does spilled gasoline evaporate more rapidly on a hot day than on a cold day?

 

9. As the temperature increases, the average kinetic energy of the molecules of gasoline increases and so a greater fraction of molecules have sufficient energy to escape from the liquid than at lower temperatures.

 

10. Carbon tetrachloride, CCl4, was once used as a dry cleaning solvent, but is no longer used because it is carcinogenic. At 57.8 °C, the vapor pressure of CCl4 is 54.0 kPa, and its enthalpy of vaporization is 33.05 kJ/mol. Use this information to estimate the normal boiling point for CCl4.

 

11. When is the boiling point of a liquid equal to its normal boiling point?

Answer(s): They are equal when the pressure of gas above the liquid is exactly 1 atm.

 

12. How does the boiling of a liquid differ from its evaporation?

 

13. Use the information in (Figure) to estimate the boiling point of water in Denver when the atmospheric pressure is 83.3 kPa.

Answer(s): approximately 95 °C

 

14. A syringe at a temperature of 20 °C is filled with liquid ether in such a way that there is no space for any vapor. If the temperature is kept constant and the plunger is withdrawn to create a volume that can be occupied by vapor, what would be the approximate pressure of the vapor produced?

 

15. Explain the following observations:

(a) It takes longer to cook an egg in Ft. Davis, Texas (altitude, 5000 feet above sea level) than it does in Boston (at sea level).

(b) Perspiring is a mechanism for cooling the body.

Answer(s): (a) At 5000 feet, the atmospheric pressure is lower than at sea level, and water will therefore boil at a lower temperature. This lower temperature will cause the physical and chemical changes involved in cooking the egg to proceed more slowly, and a longer time is required to fully cook the egg. (b) As long as the air surrounding the body contains less water vapor than the maximum that air can hold at that temperature, perspiration will evaporate, thereby cooling the body by removing the heat of vaporization required to vaporize the water.

 

16. The enthalpy of vaporization of water is larger than its enthalpy of fusion. Explain why.

 

17. Explain why the molar enthalpies of vaporization of the following substances increase in the order CH4 < C2H6 < C3H8, even though the type of IMF (dispersion) is the same.

Answer(s):Dispersion forces increase with molecular mass or size. As the number of atoms composing the molecules in this homologous series increases, so does the extent of intermolecular attraction via dispersion forces and, consequently, the energy required to overcome these forces and vaporize the liquids.

 

18. Explain why the enthalpies of vaporization of the following substances increase in the order CH4 < NH3 < H2O, even though all three substances have approximately the same molar mass.

 

19. The enthalpy of vaporization of CO2(l) is 9.8 kJ/mol. Would you expect the enthalpy of vaporization of CS2(l) to be 28 kJ/mol, 9.8 kJ/mol, or −8.4 kJ/mol? Discuss the plausibility of each of these answers.

Answer(s): The boiling point of CS2 is higher than that of CO2 partially because of the higher molecular weight of CS2; consequently, the attractive forces are stronger in CS2. It would be expected, therefore, that the heat of vaporization would be greater than that of 9.8 kJ/mol for CO2. A value of 28 kJ/mol would seem reasonable. A value of −8.4 kJ/mol would indicate a release of energy upon vaporization, which is clearly implausible.

 

20. The hydrogen fluoride molecule, HF, is more polar than a water molecule, H2O (for example, has a greater dipole moment), yet the molar enthalpy of vaporization for liquid hydrogen fluoride is lesser than that for water. Explain.

 

21. Ethyl chloride (boiling point, 13 °C) is used as a local anesthetic. When the liquid is sprayed on the skin, it cools the skin enough to freeze and numb it. Explain the cooling effect of liquid ethyl chloride.

Answer(s): The thermal energy (heat) needed to evaporate the liquid is removed from the skin.

 

22. Which contains the compounds listed correctly in order of increasing boiling points?

(a) N2 < CS2 < H2O < KCl

(b) H2O < N2 < CS2 < KCl

(c) N2 < KCl < CS2 < H2O

(d) CS2 < N2 < KCl < H2O

(e) KCl < H2O < CS2 < N2

 

23. How much heat is required to convert 422 g of liquid H2O at 23.5 °C into steam at 150 °C?

Answer(s): 1130 kJ

Evaporation of sweat requires energy and thus take excess heat away from the body. Some of the water that you drink may eventually be converted into sweat and evaporate. If you drink a 20-ounce bottle of water that had been in the refrigerator at 3.8 °C, how much heat is needed to convert all of that water into sweat and then to vapor? (Note: Your body temperature is 36.6 °C. For the purpose of solving this problem, assume that the thermal properties of sweat are the same as for water.)

 

24. Titanium tetrachloride, TiCl4, has a melting point of −23.2 °C and has a ΔH fusion = 9.37 kJ/mol.

(a) How much energy is required to melt 263.1 g TiCl4?

(b) For TiCl4, which will likely have the larger magnitude: ΔH fusion or ΔH vaporization? Explain your reasoning.

Answer(s): (a) 13.0 kJ; (b) It is likely that the heat of vaporization will have a larger magnitude since in the case of vaporization the intermolecular interactions have to be completely overcome, while melting weakens or destroys only some of them.

 

Glossary

boiling point
temperature at which the vapor pressure of a liquid equals the pressure of the gas above it
Clausius-Clapeyron equation
mathematical relationship between the temperature, vapor pressure, and enthalpy of vaporization for a substance
condensation
change from a gaseous to a liquid state
deposition
change from a gaseous state directly to a solid state
dynamic equilibrium
state of a system in which reciprocal processes are occurring at equal rates
freezing
change from a liquid state to a solid state
freezing point
temperature at which the solid and liquid phases of a substance are in equilibrium; see also melting point
melting
change from a solid state to a liquid state
melting point
temperature at which the solid and liquid phases of a substance are in equilibrium; see also freezing point
normal boiling point
temperature at which a liquid’s vapor pressure equals 1 atm (760 torr)
sublimation
change from solid state directly to gaseous state
vapor pressure
(also, equilibrium vapor pressure) pressure exerted by a vapor in equilibrium with a solid or a liquid at a given temperature
vaporization
change from liquid state to gaseous state

License

Icon for the Creative Commons Attribution 4.0 International License

Phase Transitions Copyright © by D. Latimer; D. Vanderwel; and J. Hollett is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book