Introduction to Science and Geology
Scientific Method and Geology
Learning Objectives
The goals of this chapter are to:
- Use the scientific method as practiced by geologists
- Review accuracy, precision, and extrapolation of data
0.1 The Language of Science
Science is the study of natural phenomena. The language used in science can be confusing sometimes. Many often use terms like fact, hypothesis, law, and theory to explain natural phenomena incorrectly. The distinction between these terms is subtle. Theories, laws, and facts can start as hypotheses when they are first proposed and before they are rigorously tested. Generally, a fact is a very elementary statement based on some measurement, such as water boiling at 100 °C (212 °F). A Law is based on a collection of individual facts and is an attempt (usually with mathematics) to relate one set of measurable quantities to another (mass, speed, temperature, viscosity). Example, F=ma, V = d/t, PV = nkT. A theory attempts to explain why certain laws exist and why certain facts are true under specific conditions. Example 1: Planetary orbits are elliptical (fact) because gravity is an inverse-square force (law), and matter operates under Newton’s Laws of Motion. Example 2: Matter is comprised of atoms, and this explains how gases behave (laws), why we have specific chemical reactions (laws), and why the Periodic Table exists (facts). Are some facts more certain than others? Water always boils at 100°C at sea level, but at higher altitudes, it boils at lower temperatures. So, every fact depends on the specific circumstances under which it was measured.
- Fact – A basic statement based on some measurement, experiment, or observation. All facts are true under specific conditions.
- Hypothesis – A tentative statement, such as ‘if A happens, then B must happen,’ that can be tested by direct experiment or observation. A proven hypothesis can be expressed as a law or a theory.
- Law – A logical relationship between two or more things based on facts and proven hypotheses. It is often a mathematical statement of how two or more quantities relate.
- Theory – An explanation for why certain laws and facts exist that can be tested to determine their accuracy.
- Belief – A statement that is not scientifically provable in the same way as facts, laws, hypotheses, or theories.
Exercise 0.1 – The Vocabulary of Science
Sort the statements below as an example of a fact, hypothesis, law, theory, or belief.
| The diameter of the Earth is 12,756 km (7,926 mi). | Albert Einstein explained that massive objects (like the Earth) cause a distortion in space-time, which is experienced as gravity. |
| Aliens exist. | Energy and mass can neither be created nor destroyed. |
| Water freezes at 0°C (32°F). | For every action, there is an equal and opposite reaction. |
| The position of the planets can cause humans to act in specific ways. | The bell will ring at the end of the period. |
| The universe started with a massive expansion of space and time called the Big Bang. | Species evolve. |
| The oldest layers of rock are deeper, while the youngest layers are towards the top. | Some numbers are luckier than others. |
| Students who eat breakfast will perform better on a math exam than those who do not. | Species evolve through a process known as natural selection, in which certain organisms survive and reproduce more than others. |
| There are such things as ghosts. | Drinking sugary drinks daily leads to being overweight. |
| Humans are made of cells. | Force = mass x acceleration (F=ma) |
| Students who bring their own lunch spend less money throughout the day. | A meteorite impact caused the dinosaur extinction. |
0.2 The Scientific Method
The scientific method is a step-by-step procedure that many scientists use to study the world. Often, scientists begin by observing some event or object and want to know why the event happened or why the object formed. Then, they develop a hypothesis to explain their observation and create an experiment to test the hypothesis. If the test results support the hypothesis, they develop a conclusion about the event or object. If the results don’t support the hypothesis, they go back, alter it accordingly, and retest it.
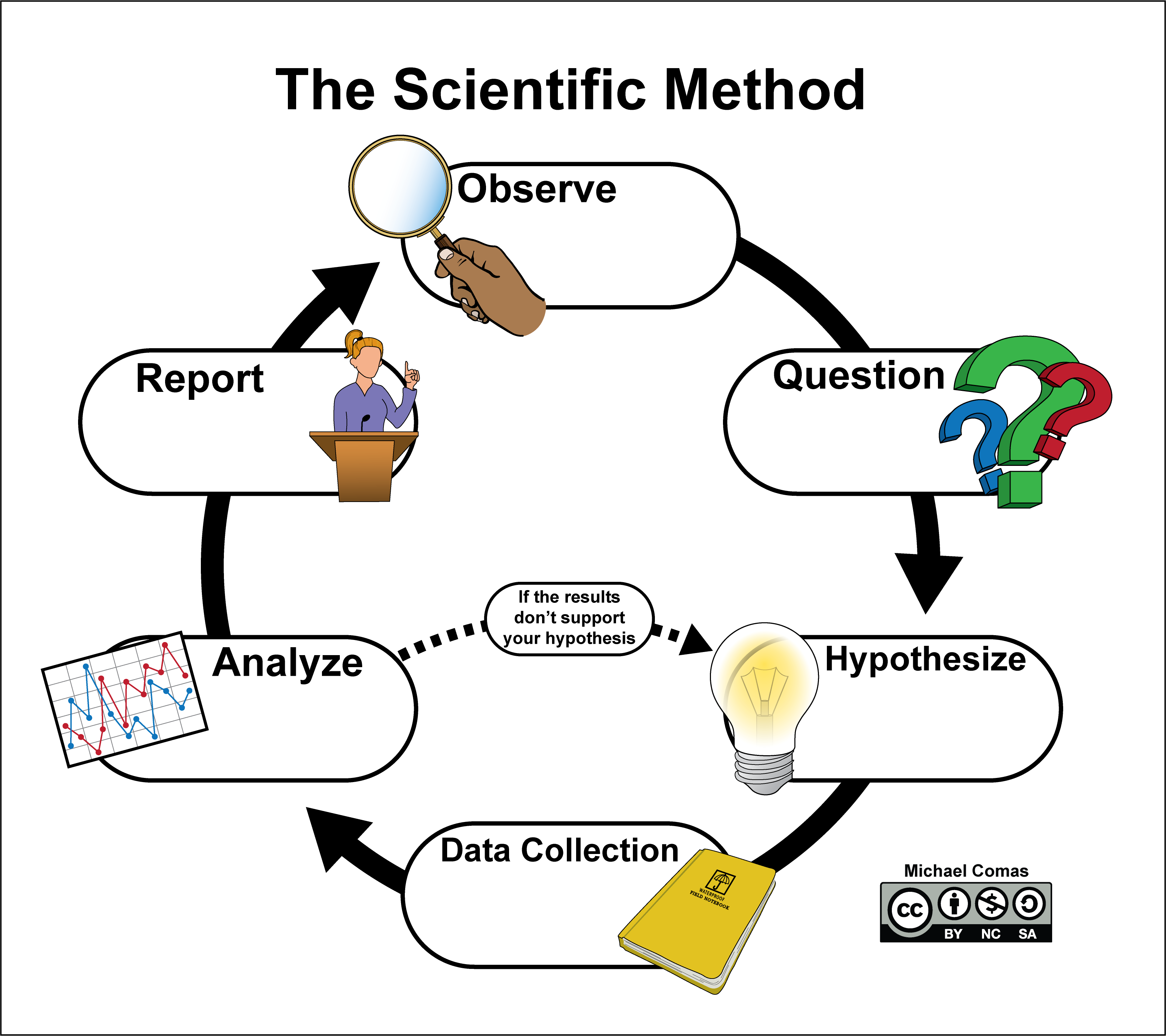
Exercise 0.2 – Everyday Use for the Scientific Method
You walk into an empty classroom and attempt to turn on the projector, but it doesn’t turn on (Figure 0.2). Use the scientific method to investigate and solve your problem. Write a statement about your issue for each step of the scientific method.

- What is your observation?
- What is your question?
- What is your hypothesis?
- What is your data?
- What is your analysis?
- What is your conclusion?
The Scientific Method and Geology
The scientific method in geology can look quite different. This is because many of the events that geologists investigate have already happened, so they can’t make any direct observations. What geologists find is the evidence left behind by that event. An example is a solidified lava flow. Geologists know the lava likely came from a volcano, but they didn’t observe the eruption and can’t test the hypothesis by creating a new eruption. They have to rely on facts they know about current lava flows and volcanic eruptions to interpret past ones. In a sense, you might consider geology to be a historical science. Geology is the intersection of the other sciences (chemistry, physics, biology, and mathematics) applied to studying the Earth.
Uncertainty
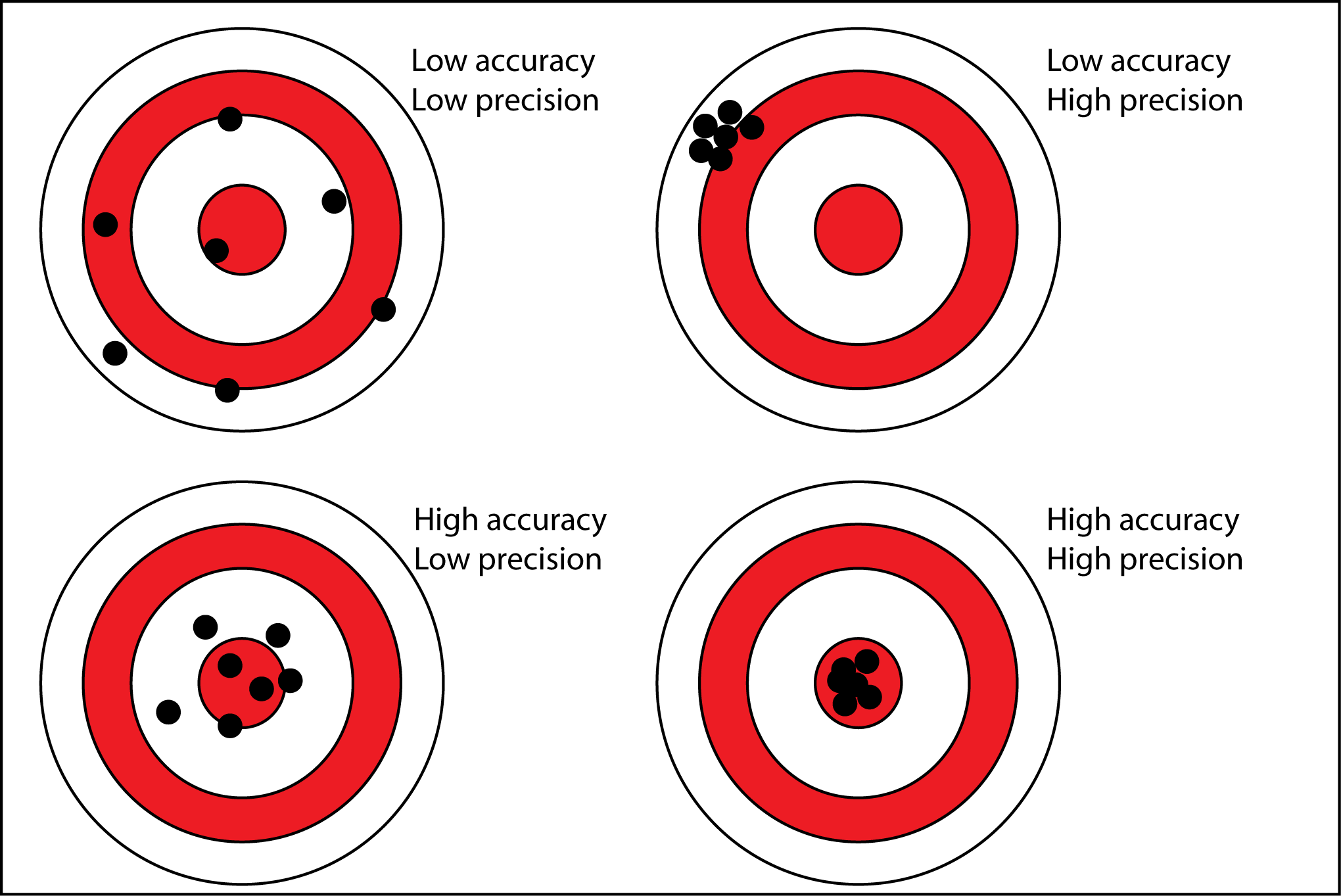
Because geologists often study past events they can’t directly observe, they must deal with uncertainty. Uncertainty in science doesn’t mean that scientists don’t believe their results or that their research is flawed. It represents natural variability in taking measurements. Often, a scientific investigation does not yield an exact measurement. Instead, scientists make repeated experiments that give a range of measurements around a central value. This is where accuracy, precision, and statistics come in (Figure 0.3). For every measurement we make, there is an actual value that we are trying to obtain. In the next exercise, you will determine the weight of a rock. Simply put, accuracy is how close a measurement is to the actual true value, whereas precision is how close those measurements tend to be to each other.
For example, if geologists are trying to figure out when a volcano erupted lava, they would radiometrically date the solidified lava flow to determine when it formed (a topic discussed later). Remember, a single measurement may not be entirely accurate; therefore, repeated measurements are necessary. If the measurements are around the same age, geologists are more certain about their results.
When doing any calculations for this or other exercises, you should consider the number of significant digits that you use. Your calculator will give you many significant digits, but these may not be appropriate for your result. The number of significant digits for your answers depends on the way you calculate. For addition and subtraction, round to the lowest significant number. For multiplication and division, your final answer should have the same number of significant digits as the least precise value given in the original problem. If you have forgotten how to do this, here is a refresher.
Exercise 0.3 – Working with Uncertainty
Your instructor has given your group a rock sample of unknown weight and an object of known weight.
- Each student should feel how heavy the object of known weight is. Then, each should heft the unknown rock sample in their hand and determine how much they think the rock weighs. Record these measurements in Table 0.1.
Table 0.1 – Rock measurements by hand Student Weight of unknown rock (g) 1 2 3 4 5 6 - What was the total range of measurements? ____________________
- What is the average of your measurements done by hand (use the appropriate significant digits)? ____________________
- Do you think your measurements are precise, accurate, both, or neither? Explain.
- Now, measure the weight of the rock sample on several scales provided by your instructor and report the results in Table 0.2.
Table 0.2 – Rock measurements by scale Scale Weight of unknown rock (g) 1 2 3 4 5 6 - What was the total range of measurements? ____________________
- What is the average of your measurements done using a scale (use the appropriate significant digits)? ____________________
- Do you think your measurements are precise, accurate, both, or neither? Explain.
- How close were your measurements done by hand to your scale measurements?
- Critical Thinking: What do you think is responsible for the differences in your measurements on the scales?
Extrapolation
Geologists often have limited data to work with when forming hypotheses and conducting analyses; after collecting data, they extrapolate their results. Extrapolation is a type of estimation based on current data. Imagine you are a geologist working in a tropical rainforest. Do you think you will find many rocks? Probably not, and if you do find any, they are likely to be in rivers. Here’s the cool part: whatever you figure out about these rocks, you can guess that the whole rainforest has the same rocks. That’s extrapolation!
0.3 The Scale of Geology
Geologists work at various scales, ranging from continents and mountain ranges to the atoms that comprise rocks and minerals. Some scales, such as geologic time, are so vast that they’re difficult to truly comprehend. The Earth is 4,540,000,000 years old. To put this into perspective, if you have a penny for every year the Earth has been around, you will have $45.4 million! More on geologic time in another chapter.
Exercise 0.4 – Distance and Scale
Geologists do a lot of measuring, whether it’s distance, age, rates, etc. They also need to convert units, especially in the United States, where the metric system is not the norm.
- The accepted age of the Earth is 4.54 billion years. If the average human lifetime is 72 years, how many human lifetimes has the Earth been around for? ____________________
- The generally accepted distance to reach outer space from the Earth’s surface is 100 km, known as the Kármán Line. What is that distance in miles? (1 km = 0.62 mi) ____________________
- The distance to the center of the Earth is 6,371 km. What is that distance in miles? ____________________
- If you could drive to the center of the Earth at a highway speed of 65 mph, how many hours would it take for you to get there? ____________________
- Open Google Earth and measure the distance from Winnipeg, MB, to Vancouver, BC, in kilometres and miles. What are the distances? ____________________
- Find a similar distance on another continent between two cities. Which two cities are they? ____________________
Additional Information
Exercise Contributions
Introduction to Science and Geology section was modified by Jessica Kristof and Ricardo L. Silva from the original Chapter 1: Introduction to Science and Geology by Daniel Hauptvogel, Virginia Sisson, Michael Comas, Somaria Sammy in Hauptvogel et al. (2024).
References
Hauptvogel, D., Sisson, V., and Comas, M. (2024). Investigating the Earth: Exercises for Physical Geology. Houston, TX: UH Libraries
an observation that's been confirmed many times so scientists can accept it as "true." But everything in science has some uncertainty; nothing is ever scientifically "true" beyond a shadow of a doubt.
an idea or proposition that can be tested by observations or experiments, about the Earth
laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena
explains known facts and also allows scientists to make predictions of what they should observe
observational error that indicates how close measurements are to their true value
observational error that indicates how close measurements are to each other.
the number of digits needed to accurately describe a measurement, starting from the first nonzero digit.

